График 2 через 2 это какой график: Что такое график работы 2 через 2 в 2021 году
График 2/2 4/4 5/2 2/2/3 что это
В России и странах СНГ существуют стандартны графиков работы для сотрудников. Согласно закону, у сотрудника должен быть выходной день в который он может восстановить силы вне зависимости от нагрузки за рабочий период. Самыми популярными на данный момент являются график 5 рабочих 2 выходных. Сегодня мы рассмотрим различные виды и определим самый оптимальный для молодого и возрастного поколения.
Виды графиков работы в России
Мы выбрали самые популярные расписания и сравнили их с размещёнными вакансиями.
График 2/2/3 как это
Этот график называют «зеркальным» т.к. он позволяет закрывать потребности компании и не нагружать сотрудника. Определяется как 2 дня рабочих, 2 выходных, 3 рабочих, 2 выходных, 2 рабочих, 3 выходных. Чаще всего присутствует в компаниях предоставляющих услуги или сервис.
График 4/4
Такой тип называется «сменный». 4 дня работаешь, 4 отдыхаешь. Обычно подходит для профессий типа: охранник, слесарь, водитель такси, курьер, упаковщик и т. п.
п.
График работы 2/1/2/3
2 дня работаешь, 1 день отдыхаешь, 2 работаешь, 3 отдыхаешь. Работодатели по такому расписанию выставляют вакансии администраторов, продавец-консультант, помощник руководителя, ведущий специалист и т.п.
График 2/2
В простонародье имеет название «2 через 2». 2 дня работаешь, 2 дня отдыхаешь. В основном подходит для грузчиков, операторов, менеджеров, водителей, нянь и прочих.
График 5/2 это как
Самое стандартное расписание рабочей недели для большинства трудящихся — это 5 дней работаешь, 2 отдыхаешь. Подходит для большинства профессий и является лидером среди возможных вариантов.
График 1/1 это как
Обычно обозначается как «сутки через сутки». Подходит вахтовый метод который сопровождается большими нагрузками. На самом деле это могут быть как 12 часов так и полный день. 1 день работаете, 1 день отдыхаете.
График 1/3
Один из самых простых рабочих графиков. Сутки (24 часа) работаете и 3 дня отдыхаете.
График 3/3
3 рабочих дня и 3 выходных. Подходит для тех кто учится или работает на других работах.
График 3/2
3 рабочих дня и 2 выходных. Сокращение выходных дней ведет к большей прибыли. 18 рабочих дней по факту из 30.
График 4/2
Один из стандартных графиков для работы компаний. 4 дня работаете и 2 дня отдых.
График 4/3
Предложенный премьер министром России Дмитрием Медведевым график не стал популярным по итогу 2020 года. В отличии от стандарта 5/2, гражданам не понравилось, что они будут получать меньше, ведь сохранять оклад по факту никто не будет.
График 6/1
Самый сложный график из всех возможных. 6 рабочих дней и всего 1 выходной. Чаще всего вызывают даже в последний день. Оплата должна быть максимальной, так же как и учет переработки сотрудника.
Чем опасен график работы 5/2 | Удивительное просто
Да, именно опасен. Хотя большая часть человечества работает именно в таком графике.
 И работает в офисе. И не подозревает об опасностях.
И работает в офисе. И не подозревает об опасностях.О да, это не такая опасность, которую представляет собой несущийся на вас разъяренный тигр. То есть мгновенно с вами не случится ничего плохого. И даже через год и через два такой жизни вы, скорее всего, останетесь более или менее здоровым и бодрым человеком.
Опасность такого графика как раз в том, что он затягивает в болото ужасно медленно и незаметно. И человек начинает считать такую жизнь нормальной. И вообще, “все так живут”.
А я считаю такую жизнь ненормальной. Почему?
5 дней человек мечтает только о том, чтобы неделя скорее закончилась. Он ждет пятницы. Он ждет, а не живет.
Видели в интернете мемы: о, наконец-то пятница! Их много вариантов. Но суть одна: пятница – это жизнь.
И что тут начинается? Правильно, расслабление, и чаще всего алкогольное. У Семена Слепакова есть даже такая песня “Каждую пятницу я в г. .. (Дзен не любит это слово)”. Собственно, основная масса работников 5/2 так и развлекается.
.. (Дзен не любит это слово)”. Собственно, основная масса работников 5/2 так и развлекается.
И даже если не так. Наработавшийся 5 дней человек к субботе имеет только одно желание – поспать. И он 2 дня отсыпается и отдыхает лежа или сидя.
Еще из развлечений выходного дна можно назвать уборку в квартире. А когда еще? Всю неделю не до этого.
А в воскресенье вечером наш работник с тоской смотрит на календарь и понимает, что завтра снова понедельник.
И так всю жизнь.
Человек всю неделю ждет пятницы и собственно жить-то он и не успевает. Ну разве можно назвать жизнью сонно-уборочные выходные? А на большее у нашего работника не хватает ни сил, ни желаний. И чем старше он становится, тем меньше и сил и желаний.
Для того, чтобы жить полной жизнью, график 5/2 решительно не подходит. Я уже писала об этом в статье “С чего начинается активный отдых”. Те, кто начинает это понимать, потихоньку задумываются о смене графика или переходе на удаленку.
Те, кто начинает это понимать, потихоньку задумываются о смене графика или переходе на удаленку.
Тогда возможностей для жизни становится значительно больше. Для яркой, насыщенной, активной жизни.
Для нормальной жизни. Потому что только такую жизнь я могу назвать нормальной.
А сонно-уборочно-телевизионно-алкогольные выходные – это на мой взгляд полнейшее убожество и прижигание времени. Бесценного и невозвратимого времени. Самого ценного ресурса, который у нас есть.
Пока есть.
А вы как живете?
Подписывайтесь на Удивительное просто и живите осознанной и полной жизнью.
О пользе/вреде графика работы или “2 через 2” vs “пятидневка”
← →xayam © (2012-11-22 13:40) [0]
Давно задумываюсь о таких вещах.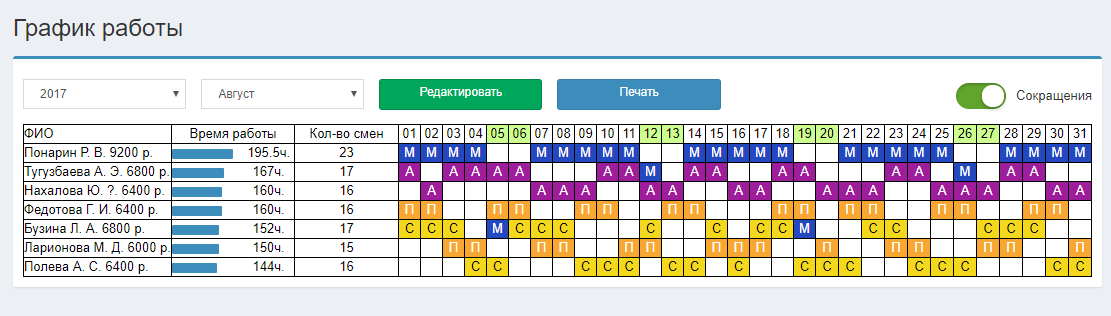
Тем более у нас большинство перевели на пятидневку с выходными в разные дни недели.
Хотя сам большую часть проработал на 2 через 2, считая это очень удобным графиком.
Буду признателен, если подскажите, проводились ли какие-то серьёзные исследования о влиянии графика работы на человека в долгосрочной перспективе? Научный подход, статистика желательно какая-то.
Сам считаю, что пятидневка – неестественный график, а когда выходные дни раздельно, еще не суббота или воскресенье, то такой график “разрывной” грубо говоря, работал так несколько месяцев – самые негативные воспоминания.
← →
БарЛог © (
И так, и так работал – ко всему привыкаешь.
ЗЫ. Пишется “Кунг-фу”.
ЗЗЫ. http://www.youtube.com/watch?v=pGFf3SRP1bE 😉
← →
Плохиш © (2012-11-22 13:46) [2]
> Сам считаю, что пятидневка – неестественный график, а когда
> выходные дни раздельно, еще не суббота или воскресенье,
> то такой график “разрывной” грубо говоря, работал так несколько
> месяцев – самые негативные воспоминания.
Вроде буквы знакомые и в слова знакомые складываются, а вот что написано нифига не понял.
← →
TUser © (2012-11-22 13:50 ) [3]
> Буду признателен, если подскажите, проводились ли какие-
> то серьёзные исследования о влиянии графика работы на человека
> в долгосрочной перспективе? Научный подход, статистика желательно
> какая-то.
Есть опыт перехода на пятидневку – 4 дня работаем, 1 отдыхаем. Каждый день отдыхает 20% работников. Быстро отказались. Поиск по словам типа “непрерывное производство, советский революционный календарь”.
← →
xayam © (2012-11-22 13:54) [4]
> а вот что написано нифига не понял
написал, что пятидневка тоже разная бывает.
Есть график, когда выходные суб/воскр, а есть так что выходных два, но любой день недели, причем у твоего коллеги эти дни другие
> Пишется “Кунг-фу”
слушай беззвучие 🙂 то есть то что не написано
> www.
 youtube.com/watch?v=pGFf3SRP1bE
youtube.com/watch?v=pGFf3SRP1bEэтой философии очень соответствует мелодия “Flow like water”
← →
Аббат Пиккола (2012-11-22 14:16) [5]
Исход (31:13-17):
Скажи сынам Израилевым так: cубботы Мои соблюдайте
← →
xayam © (2012-11-22 14:16) [6]
> TUser © (22.11.12 13:50) [3]
но речь не о пятидневной недели, а обычной 7-и = 5 рабочих + 2 выходных
← →
Думкин © (2012-11-22 14:41) [7]
У нас в школе был: ПВС – рабочие, Ч – типа выходной(факультативный день), ПС – рабочие, В – выходной. Удобно.
← →
RDen © (2012-11-22 14:57) [8]
>xayam © (22. 11.12 13:40)
11.12 13:40)
а два через два, это по сколько часов смена?
← →
xayam © (2012-11-22 15:01) [9]
> а два через два, это по сколько часов смена?
12 часов
у меня с 10-00 до 22-00
← →
RDen © (2012-11-22 15:09) [10]
ну если не обременён семейной жизнью, то наверное удобно – у меня щя жена вынуждена работать 4/2 (естественно выходные со мной 5/2 часто не совпадают), что не совсем удобно (а иногда и удобно)))
← →
xayam © (2012-11-22 15:15) [11]
> ну если не обременён семейной жизнью
я нет, но даже по опыту общения с другими: семейным график тоже подходит/нравится/устраивает
← →
QAZ9 (2012-11-22 15:26) [12]
самый ништяк это сутки через трое причем в большинстве случаев там можно и поспать ночью
← →
xayam © (2012-11-22 15:29) [13]
> самый ништяк это сутки через трое причем в большинстве случаев
> там можно и поспать ночью
+1
причем “сутки через трое” это практически те же “2 через 2”, только один из дней перенесён на ночь
← →
RDen © ( 2012-11-22 15:51) [14]
на сколько мне известно (не заглядывая во всякие там вики. .и прочие педии)), график 5/2 (и не по 12 часов) с выходными в Сб и Вс, вырабатывался годами исходя из допустимых физических и прочих нагрузок на организм человека
.и прочие педии)), график 5/2 (и не по 12 часов) с выходными в Сб и Вс, вырабатывался годами исходя из допустимых физических и прочих нагрузок на организм человека
← →
БарЛог © (2012-11-22 15:52) [15]
QAZ9 (22.11.12 15:26) [12]
Обычно при таких графиках зарплата – 30-50 тыс. (в Москве)
← →
Jeer © (2012-11-22 16:43) [16]
Да мне вообще работать давно не хочется, вот и не работаю.. или, почти.
Три еще года, а тогда и пошло оно в обратно 🙂
← →
Пит (
> Хотя сам большую часть проработал на 2 через 2, считая это
> очень удобным графиком.
ясен пень.
При 5/2 у тебя 8-9 выходных дней в месяц.
При 2/2 у тебя 15 выходных в месяц ))
← →
RDen © (2012-11-22 17:20) [18]
>Пит (22.11.12 16:57) [17]
одинаково (в переводе на часы рабочего/не рабочего времени))
← →
xayam © (2012-11-22 17:26) [19]
> одинаково (в переводе на часы рабочего/не рабочего времени))
рабочие/нерабочие одинаково, но стоит учесть еще то, что часто работа не через дорогу, и траты денег/времени на дорогу больше на пятидневке.
← →
MsGuns © (2012-11-22 17:31) [20]
ИМХО, сильно зависит от самого человека + специфика работы.
По молодости полюблял вахтовый – отбатрачил 2 недели по 12ч, потом две недели дома, особенно если работа типа дежурства.
Потом пришлось на конверйере работать по разносменной схеме – сгначала показалось круто, через пару месяцев волком взвыл.
Со временем понял, что ничего лучше “стандартной” пятидневки с 8-ми (с обедом 8,45) часовым рабочим днем и укороченной пятницы не придумали. Во-первых, потому что он физиологически оптимален, во-вторых, вся жизнь вокруг (работа банков, торговли, сферы услуг и т.д.) заточена именно под такой график.
Хуже всего т.н. свободный режим работы, т.е. когда на работу вообще не надо ходить (например если эта самая работа на дому) или когда свободное посещение. Тут очень быстро можно тупо осоловеть от лени.
Но все, повторяю, сугубо индивидуально, конечно
← →
RDen © (2012-11-22 17:49) [21]
>xayam © (22.11.12 17:26) [19]
> но стоит учесть еще то, что часто работа не через дорогу
и при этом ещё учитывается:
> и траты денег/времени на дорогу больше на пятидневке.
то ИМХО на фих такая работа
← →
брат Птибурдукова (2012-11-22 17:51) [22]
> вся жизнь вокруг (работа банков, торговли, сферы услуг и
> т.д.) заточена именно под такой график
то есть они работают, когда работаешь ты, а когда ты заканчиваешь, то и они уже закрыты…
← →
RDen © (2012-11-22 18:13) [23]
>брат Птибурдукова (22.11.12 17:51) [22]
всё меньше замечаю такое соответствие – куда и во сколько не приди – везде толпы народу – ощущение, что ваще ни кто не работает
← →
QAZ9 (2012-11-22 18:30) [24]
> БарЛог © (22.11.12 15:52) [15]
а это много или мало? у нас при любом графике такие цифры маловероятны 🙂
я например предпочту отдежурить в котельной 1\3, чем быть офисным планктоном 5\2 с вариантом “а вдруг в конце дня придет заказчик и его надо облизать со всех сторон”, тем более что зарплаты одинаковые
←
RDen © (2012-11-22 18:35) [25]
>QAZ9 (22. 11.12 18:30) [24]
11.12 18:30) [24]
а вдруг в конце дня придет ЖД состав с углём для котельной?
← →
Пит (2012-11-22 18:43) [26]
> одинаково (в переводе на часы рабочего/не рабочего времени))
глупо оценивать эффективность / результат работы по проведенным часам в офисе ) Хотя в России я не видел чтобы по другому умели оценивать. Дальше контроля времени мало кто заходит, это только в пивнушке все очень умные и рассуждают про мотивацию, внутренний стандарт качества и бла бла бла.
А как нужно управлять людьми, так почему-то сразу большинство ничего больше, чем палочную систему реализовать не может. Парадокс? )
← →
картман © (2012-11-22 18:44) [27]
самый ништяк: 4 + 3, но он нам только снится
← →
Kerk © (2012-11-22 18:52) [28]
Пит (22. 11.12 18:43) [26]
11.12 18:43) [26]
> Дальше контроля времени мало кто заходит, это только в пивнушке
> все очень умные и рассуждают про мотивацию, внутренний стандарт
> качества и бла бла бла.
>
> А как нужно управлять людьми, так почему-то сразу большинство
> ничего больше, чем палочную систему реализовать не может.
> Парадокс? )
Не парадокс. Одно дело пивнушка, а другое – когда на тебя давит ответственность за результат. В совокупности с тем, что IT-шников управлять людьми как правило не учат, имеем то, что имеем.
Но на самом деле могу сходу назвать штуки 3 компании, которые в России дают довольно гибкий график для разработчиков. Это сходу, если покопаться в памяти, наверно больше будет.
← →
RDen © (2012-11-22 18:54) [29]
>Пит (22.11.12 18:43) [26]
не скажу за пивнушки – не хожу туда, но да, хотя и с не большим успехом, но пытаюсь доказать начальству:
твоё же >глупо оценивать эффективность / результат работы по проведенным часам в офисе
но Катя, Маша, от звонка до звонка, с рабочим расписанием – маникюр, перекур, обед, парикмахерская, аптека, игры и оставшееся “рабочее” время, под названием – скоро домой, получают гораздо меньше претензий, чем я – опадающий/ушедший раньше на пол часа. .
.
хотя на прямой мой вопрос (на всеобщей линейке) – а что то не делается с моей стороны – начальство затыкается…
← →
Пит (2012-11-22 18:55) [30]
RDen, ты из Екатеринбурга, видимо?
Слушай, а как население на самом деле относится к Ройзману? ) А то вот читаешь всякое, страсти такие там у вас, интересно обывательское, сори что не в тему)
← →
RDen © (2012-11-22 19:05) [31]
>Пит (22.11.12 18:55) [30]
да, Ёбург, слушай, уже не знаю как расценивать…
Вроде и доводы уже представляют весомые не в их пользу…
но.. наркота – бабло в карман, сам наверное догадываешься кому
← →
Пит (2012-11-22 19:09) [32]
> Одно дело пивнушка, а другое – когда на тебя давит ответственность
> за результат
понятно. Но вроде все такие умные, когда разговаривают. Допустим, типичнейшая ошибка – заставлять человека работать больше, быстрее, но при этом требовать такого же качества, вдумчивости, анализа и так далее. В общем, обычно описывается как голубая мечта менеджеров – за те же деньги получить в два раза больше.
Но вроде все такие умные, когда разговаривают. Допустим, типичнейшая ошибка – заставлять человека работать больше, быстрее, но при этом требовать такого же качества, вдумчивости, анализа и так далее. В общем, обычно описывается как голубая мечта менеджеров – за те же деньги получить в два раза больше.
Ладно менеджер, ему всегда кажется, что тут делать нечего, раз два и все готово. Но ведь начальники IT-отделов страдают тем же самым. Когда речь о них самих как разработчиков – полное понимание вопроса, когда нужно требовать от других – так сразу те же голубые мечты. Причем, получают конфликты, падение эффективности, все блага в общем – и нет, из раза в раз одно и то же. Есть что-то такое в человеке )
Насчет IT – а тут мне кажется дело даже лучше обстоит, люди неглупые и на настоящий момент в целом высокодоходная профессия, профи – в дефиците большом. Так что особо жестить не получится, человек просто пошлет и выберет другого работодателя. Но точно такие же типичные ошибки происходят и в других секторах, один в один.
А самое прикольное – сами подчиненные считают это нормальным и если начальник не орет на всех хотя бы периодически – считают его мягкохарактерным и собственно перестают уважать, сливают, считают несправляющимся со своими обязанностями. Реально это наблюдал, жесть какая-то, рабоче-крестьянский мазохизм. Люди гораздо проще воспримут, если начальник им в рожу даст, а потом коньяком вину загладит, получится “А че, нормальный мужик, иногда бывает вспылит”. А вот стабильность, планомерность, качество – это какие-то “европейские” ценности, чуждо нам типо. Странно это все
← →
Пит (2012-11-22 19:11) [33]
> да, Ёбург, слушай, уже не знаю как расценивать…
то есть, в целом среди населения разные мнения, говорят всякое типа?
← →
RDen © (2012-11-22 19:19) [34]
>Пит (22. 11.12 19:09) [32]
11.12 19:09) [32]
>А вот стабильность, планомерность, качество – это какие-то “европейские” ценности, чуждо нам типо. Странно это все
всё нормально, по нашему, на лечение ребёнка родители со слезами собирают копейки на лечение ЗА ГРАНИЦЕЙ. Сегодня был с ребёнком в травмпункте – руку вчера сломала на физкультуре – очередь 35 чел. – один кабинет работает. Гардероб и туалет – не работают..
а вообще смотри первый канал – новости – фсё отлично!
← →
Пит (2012-11-22 19:30) [35]
> руку вчера сломала на физкультуре – очередь 35 чел. – один
> кабинет работает. Гардероб и туалет – не работают..
ну тут мы бесконечный флуд может развести. Медицина – тема к этому располагающая.
Вот недавно бывшая однокурсница писала, она в Америку продолжать учиться уехала, ну там аспирантура и все такое. Говорит, с велосипеда упала, что-то спина стала побаливать, сходила на рентген. Очередей – ноль, все улыбаются, все круто. За 10 минут все сделали, снимок – перелома нет, хорошо. Счет выставили: порядка 600 баксов.
Очередей – ноль, все улыбаются, все круто. За 10 минут все сделали, снимок – перелома нет, хорошо. Счет выставили: порядка 600 баксов.
Не развод, вроде как узнала – вполне стандартная цена. Очень надеется, что её страховка покроет эту сумму. Это у неё еще все официально, студенческая ученическая виза (или какая там дается), официальная работа при институте и бла бла.
В следующий раз уже просто так к врачу не пойдет, будет долго думать и рассчитывать. Особенно, в контексте мед. страховки, там говорят без поллитры вообще не разберешь. А у многих страховки просто тупо нету, она не обязательно полагается, это при найме именно весомый доп. соц. мотиватор, обычно у крупных контор. Пойдет, видимо, если совсем хреново станет, а так – себе дороже.
Так что везде по разному со своими плюсами, минусами.
← →
Kerk © (2012-11-22 19:34) [36]
> Пит (22. 11.12 19:09) [32]
11.12 19:09) [32]
Задачи разные.
Программисты хотят писать хороший код, а у бизнеса есть сроки, привязанные к финансовым целям, которые чаще всего не с потолка берутся, к слову. Менеджеру среднего звена приходится лавировать между спущенными сверху целями и хотелками программистов, идя на компромиссы.
И если его еще не уволили, а у бизнеса есть деньги на выплату программистам их немаленьких на общем фоне зарплат, то видимо не так уж плохо он со своей работой справляется.
В целом, я бы не сказал, что у нас есть какая-то особая местная специфика. Скорее многое можно списать на молодость IT в стране. Средний возраст отрасли (если отбросить тех, кто в 90м году забыл из НИИ уволится) – курам на смех. Отсюда многие проблемы.
← →
RDen © (2012-11-22 19:38) [37]
>Пит (22.11.12 19:30) [35]
бесконечный флуд в Госдуме..
чуть добавлю:
а вообще смотри первый канал – новости – у нас фсё отлично, у “них” – фсё плохо))
← →
Пит (2012-11-22 19:53) [38]
> а у бизнеса есть сроки, привязанные к финансовым целям,
это очевидная истина.
Но ведь речь и идет об эффективности и о решениях, которые как раз вредят эффективности. Менеджер делает так, что проект в результате будет плохим, долго делающимся и так далее. Иными словами обеспечивается плохая конвертируемость денег в работу, низкая эффективность этого процесса. Как раз бизнесу это и не нужно.
Думаю, в твоих книжках, которые ты читаешь, наглядно показывалось как снижение качества кода ниже внутреннего у человека качества негативно сказывается в результате на сроках, даже при согласии бизнеса на данное качество.
Помню был отличный пример, когда менеджер действительно грамотно расчитал и развел проект, сдача была назначена на 1 июня. Когда руководство узнало, что все идет по плану – то срок сдачи…. Бинго бонго – перенесли на 1 мая! Вроде бы типичнейшая же ошибка, простецкая, но найди бизнес, который не повторит эту ошибку? )
И что будет с этим отличным менеджером (выдержать срок – это круто)? Он или уйдет из компании, или не будет больше говорить правду руководству, ведь тоже абсолютно очевидно.
Поэтому речь как раз о действиях, которые в результате СНИЖАЮТ эффективность разработки. И это начинает походить на какой-то анекдот “Мы выбираем долго и фигово, чем быстро и хорошо”
← →
RDen © (2012-11-22 20:15) [39]
>Пит (22.11.12 19:53) [38]
ну менеджер (это вообще кто такой по русски?) и рассчитал и развёл проект не правильно. Надо было на сентябрь.
и никакого …. Бинго бонго
← →
Барлог_ (2012-11-22 20:21) [40]
QAZ9 (22.11.12 18:30) [24]
Если драйверы умеешь устанавливать,то 50 можно получать, если наглости хватит такое место найти и устроиться.
35 – вообще запросто (куча вчерашних студентов)
| |||||
| ✎ New thread | Private message | Name | Date | |||
| 01.2022 2:00:02″>824 | 14704 | Ошибки в словаре | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 all | 4uzhoj | 23.02.2021 | 13:36 |
| 50 | 630 | Помогите пожалуйста перевести фразу с английского вопрос из теста | 1 2 all | Incredible | 13.01.2022 | 13:48 |
| 3 | 127 | Помогите разобраться с пословицами, пожалуйста! | krstphr1 | 15.01.2022 | 15:10 |
| 7 | 2022 18:07:06″>138 | hilar shadow медицинский термин в рентгене | ekaterina_ukr | 15.01.2022 | 20:29 |
| 2 | 107 | ОФФ: горизонтальная черта в начертании символов | Lapelmike | 16.01.2022 | 11:40 |
| 4 | 159 | Помогите расшифровать, пожалуйста! | mikhail93 | 15.01.2022 | 14:20 |
| 6 | 236 | grace time | displacedbones | 13.01.2022 | 20:36 |
| 01.2022 19:44:35″>4 | 157 | Помогите перевести, пожалуйста! | SagaSaga | 14.01.2022 | 15:31 |
| 6 | 180 | Прошу помощи – cutest | Посторонним_В | 14.01.2022 | 15:54 |
| 12 | 185 | prevent the widening of a global decarbonisation divide | adelaida | 13.01.2022 | 16:43 |
| 2 | 141 | Просадка пола | dimawww3 | 13.01. 2022 2022 |
16:18 |
| 9 | 274 | Прошу помощи / Нотариат нем-англ / “отпечатан только на одной стороне листа” | Mme Kalashnikoff | 12.01.2022 | 15:32 |
| 7 | 193 | operational support | krisstte | 11.01.2022 | 14:39 |
| 29 | 490 | Mouth operated bib cock | zhigansky | 8.01.2022 | 12:57 |
| 6 | 171 | аs a commercial gesture | Arima | 12. 01.2022 01.2022 |
10:23 |
| 5 | 189 | VSAP | Gohar_85 | 12.01.2022 | 17:45 |
| 7 | 257 | помогите, пожалуйста, перевести | teachengl16 | 12.01.2022 | 10:24 |
| 621 | 20265 | Проблемы в работе нового сайта | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 all | 4uzhoj | 15.05.2019 | 11:05 |
| 10 | 185 | механическая вентиляция легких | costyan | 11. 01.2022 01.2022 |
16:08 |
| 6 | 219 | Обучающиеся ВУЗов и ССУЗов | Nick02 | 11.01.2022 | 13:35 |
| 102 | 2244 | Транскрипция | 1 2 3 all | aksa | 12.11.2021 | 23:21 |
| 22 | 819 | защита проекта | 1 2 all | VictorMashkovtsev | 11.08.2019 | 10:43 |
| 5 | 135 | rebor | Ying | 11.01.2022 | 3:12 |
График 2\2\3
- Форум
- Архив
- Образование и работа
Открыть тему в окнах
Никто не сталкивался ? Мне говорят что это например понед.
 вторник.- работаешь , среда четверг -выходной , пятница ,суббота и воскресенье работаешь . Ну помоему это нереально так работать — каждая пят.субб.воскр работа . Мне кажется это всё таки как плавующие т.е сначала два рабочих , два выходных , три рабочих , дальше два выходных , два рабочих , три выходных . А вы как думаете ? Кто сталкивался с таким графиком ?
вторник.- работаешь , среда четверг -выходной , пятница ,суббота и воскресенье работаешь . Ну помоему это нереально так работать — каждая пят.субб.воскр работа . Мне кажется это всё таки как плавующие т.е сначала два рабочих , два выходных , три рабочих , дальше два выходных , два рабочих , три выходных . А вы как думаете ? Кто сталкивался с таким графиком ?Второй вариант (1-я неделя: пн-вт рабочие, ср-чт выходные, пт-сб-вск рабочие. 2-я неделя: пн-вт выходные, ср-чт рабочие, пт-сб-вск выходные) я работала, удобно. Только тяжело 3 рабочих дня подряд выдерживать.
Второй вариант.
Первая неделя работаете пять дней, вторая неделя – два дня.Чудесный график.
 Первая неделя пять дней работаешь, вторую – только два, просто прелесть!
Первая неделя пять дней работаешь, вторую – только два, просто прелесть!Вы серьёзно , а вас не смушает что пять рабочих дней получается по 10-12 часов . Т.к рабочие часы обозначены с 10 до 21-22 часов .
У меня знакомые так работают по графику: короткая и длинная неделя. очень они довольны и спокойно относятся к тому, что надо раюотать с 10 до 22. Но у них и работа не такая активная, больше сидячая. Если бы приходилось работать все часы на ногах, то не вариант, мне кажется.
Ну скорее как вариант при сидячей менее подвижной работе .
 Думаю продавцом в магазине тяжеловато , три дня на ногах с утра до вечара .
Думаю продавцом в магазине тяжеловато , три дня на ногах с утра до вечара .Нет, не смущает. Пять дней не подряд же. Если б подряд, то тяжело, конечно.
Прекрасный график, работала. Иногда и выходные и праздники попадают, ничего страшного, зато все успеваешь на неделе все дела сделать, а через неделю только 2 рабоч дня. Супер.
Графики линейных уравнений
График линейного уравнения с двумя переменными представляет собой прямую (поэтому его и называют линейный ).
Если вы знаете, что уравнение является линейным, вы можете построить его график, найдя любые два решения.
( Икс 1 , у 1 ) и ( Икс 2 , у 2 ) ,
начертить эти две точки и провести линию, соединяющую их.
Пример 1:
Нарисуйте уравнение Икс + 2 у знак равно 7 .
Можно найти два решения, соответствующие Икс -перехватывает и у -перехватывает графика, установив сначала Икс знак равно 0 а потом у знак равно 0 .
Когда Икс знак равно 0 , мы получили:
0
+
2
у
знак равно
7
у
знак равно
3. 5
5
Когда у знак равно 0 , мы получили:
Икс + 2 ( 0 ) знак равно 7 Икс знак равно 7
Итак, две точки ( 0 , 3,5 ) и ( 7 , 0 ) .
Отметьте эти две точки и проведите линию, соединяющую их.
Если уравнение находится в форма пересечения наклона или точечно-наклонная форма , вы также можете использовать склон чтобы помочь вам график.
Пример 2:
График линии у знак равно 3 Икс + 1 .
Из уравнения мы знаем, что
у
-перехват
1
, смысл
(
0
,
1
)
и наклон
3
. Нарисуйте точку
(
0
,
1
)
и оттуда вверх
3
единиц и вправо
1
единицу измерения и нанесите на график вторую точку. Нарисуйте линию, содержащую обе точки.
Нарисуйте точку
(
0
,
1
)
и оттуда вверх
3
единиц и вправо
1
единицу измерения и нанесите на график вторую точку. Нарисуйте линию, содержащую обе точки.
Горизонтальные и вертикальные линии имеют дополнительные простые уравнения.
Пример 3:
Горизонтальная линия: у знак равно 3
Вертикальная линия: Икс знак равно − 2
2: Отображение точек и линий в двух измерениях
2: Отображение точек и линий в двух измерениях — Математика LibreTexts Перейти к основному содержанию- Последнее обновление
- Сохранить как PDF
- 2.
 1: Примеры для дальнейшего
1: Примеры для дальнейшего
- 2.
- 2.2: Поиск остатков
- В части статистики линейной регрессии нас часто просят найти остатки. Учитывая точку данных и линию регрессии, невязка определяется вертикальной разницей между наблюдаемым значением y и y на основе уравнения линии регрессии.
- 2.3: Найдите уравнение линии по ее графику
- Существует два основных способа представления линии: первый — с помощью графика, а второй — с помощью уравнения.В этом разделе мы будем практиковаться, как найти уравнение линии, если нам дан график линии. Два ключевых числа в уравнении линии — это наклон и точка пересечения с осью y. Таким образом, основными шагами в нахождении уравнения линии являются нахождение наклона и нахождение точки пересечения с осью y. В статистике нам часто представляют диаграмму рассеяния, на которой мы можем видеть линию.
- 2.
 4: Найти y по x и уравнению прямой
4: Найти y по x и уравнению прямой - Линию можно рассматривать как функцию, что означает, что если задано значение x, уравнение прямой дает ровно одно значение у; Это особенно полезно в регрессионном анализе, где линия используется для предсказания одной переменной с учетом значения другой переменной.
- 2.
- 2.5: Нарисуйте линию по ее уравнению
- Часто нам дают уравнение линии, и мы хотим его визуализировать. По этой причине важно иметь возможность изобразить линию по ее уравнению. Мы рассмотрим линии, которые находятся в форме точки пересечения наклона: y=a + bx, где a — точка пересечения линии по оси y, а b — наклон линии. Y-перехват — это значение пересечения линии с осью y. Уклон – это подъем над пробегом.
- 2.6: Интерпретация наклона линии
- Распространенная проблема, когда мы изучаем уравнение линии в алгебре, заключается в том, что мы заявляем наклон как число, но понятия не имеем, что он представляет в реальном мире.
 Наклон линии – это подъем над разбегом. Если наклон задан целым или десятичным значением, мы всегда можем поместить его над числом 1. В этом случае линия поднимается на наклон, когда она проходит 1. «Проходит 1» означает, что значение x увеличивается на 1 единицу. Следовательно, наклон показывает, насколько изменяется y при изменении x на 1 единицу.
Наклон линии – это подъем над разбегом. Если наклон задан целым или десятичным значением, мы всегда можем поместить его над числом 1. В этом случае линия поднимается на наклон, когда она проходит 1. «Проходит 1» означает, что значение x увеличивается на 1 единицу. Следовательно, наклон показывает, насколько изменяется y при изменении x на 1 единицу.
- 2.7: Интерпретация точки пересечения линии по оси Y
- Подобно наклону линии, многие классы алгебры рассматривают точку пересечения линии по оси Y, не объясняя, как ее использовать в реальном мире. Точка пересечения линии по оси Y — это значение \(y\), где линия пересекает ось Y. Другими словами, это значение \(y\), когда значение \(x\) равно 0. Иногда это имеет истинное значение для модели, которую предоставляет линия, но иногда это бессмысленно.В этом разделе мы встретим примеры обоих типов.
- 2.8: Начертите упорядоченную пару
- Мы уже подробно рассмотрели, как наносить точки на числовую прямую, и это очень полезно для представления одной переменной.
 Теперь мы перейдем к вопросам, которые предполагают сравнение двух переменных. Работа с двумя переменными часто встречается в статистических исследованиях, и мы хотели бы иметь возможность отображать результаты графически. Лучше всего это сделать, нанеся точки в плоскости xy.
Теперь мы перейдем к вопросам, которые предполагают сравнение двух переменных. Работа с двумя переменными часто встречается в статистических исследованиях, и мы хотели бы иметь возможность отображать результаты графически. Лучше всего это сделать, нанеся точки в плоскости xy.
Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet
Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения представляет собой набор точек на координатной плоскости, все из которых являются решениями уравнения. Если все переменные представляют действительные числа, можно построить уравнение, нанеся достаточное количество точек для распознавания шаблона, а затем соединив точки, чтобы включить все точки.
Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
Пример
Привить функцию y = x + 2
Начните с выбора нескольких значений x, например. -2, -1, 0, 1 и 2 и вычислить соответствующие значения y.
| Х | Y = х + 2 | Заказанная пара |
| -2 | -2 + 2 = 0 | (-2, 0) |
| -1 | -1 + 2 = 1 | (-1, 1) |
| 0 | 0 + 2 = 2 | (0, 2) |
| 1 | 1 + 2 = 3 | (1, 3) |
| 2 | 2 + 2 = 4 | (2, 4) |
Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость
На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.
Проведя линию через все точки и продолжая линию в обоих направлениях, мы получим противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.
Если вы хотите использовать только две точки для определения линии, вы можете использовать две точки, где график пересекает оси. Точка пересечения графика с осью x называется точкой пересечения графика с осью y, а точка пересечения графика с осью y называется точкой пересечения графика с осью y.Пересечение x находится путем нахождения значения x, когда y = 0, (x, 0), а пересечение y находится путем нахождения значения y, когда x = 0, (0, y).
Стандартная форма линейного уравнения
$$Ax+By = C,\: \: A,B\neq 0$$
Прежде чем построить линейное уравнение в его стандартной форме, сначала нужно решить уравнение относительно y.
$$2y-4x=8$$
$$2y-4x\, {\color{green} {+\, 4x}}=8\, {\color{green} {+\, 4x}}$$
$$2г=4x+8$$
$$\frac{2y}{{\color{green} 2}}=\frac{4x}{{\color{green} 2}}+\frac{8}{{\color{green} 2}} $$
$$y=2x+4$$
Отсюда вы можете построить уравнение, как мы это сделали в примере выше.
График y = a представляет собой горизонтальную линию, где линия проходит через точку (0, a)
Принимая во внимание, что график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)
Видеоурок
Нарисуйте график линейного уравнения y =3x – 2
Графики линейных уравнений с двумя переменными — Промежуточная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Точки графика в прямоугольной системе координат
- График линейного уравнения путем построения точек
- График вертикальных и горизонтальных линий
- Найдите точки пересечения x и y
- Нарисуйте линию, используя точки пересечения
Прежде чем начать, пройдите этот тест на готовность.
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить для y :
Если вы пропустили эту проблему, просмотрите (рисунок).
Точки графика в прямоугольной системе координат
Точно так же, как карты используют сетку для определения местоположений, сетка используется в алгебре для отображения взаимосвязи между двумя переменными в прямоугольной системе координат.Прямоугольную систему координат также называют плоскостью xy или «координатной плоскостью».
Прямоугольная система координат образована двумя пересекающимися числовыми линиями, одной горизонтальной и одной вертикальной. Горизонтальная числовая линия называется осью x . Вертикальная числовая линия называется осью y . Эти оси делят плоскость на четыре области, называемые квадрантами. Квадранты обозначены римскими цифрами, начиная с верхнего правого угла и продолжая против часовой стрелки.См. (Рисунок).
Эти оси делят плоскость на четыре области, называемые квадрантами. Квадранты обозначены римскими цифрами, начиная с верхнего правого угла и продолжая против часовой стрелки.См. (Рисунок).
В прямоугольной системе координат каждая точка представлена упорядоченной парой. Первое число в упорядоченной паре – это x -координата точки, а второе число – y -координата точки. Фраза «упорядоченная пара» означает, что важен порядок.
Заказанная пара
Упорядоченная пара дает координаты точки в прямоугольной системе координат. Первое число — это координата x .Второе число — это координата y .
Какова упорядоченная пара точек пересечения осей? В этой точке обе координаты равны нулю, поэтому ее упорядоченная пара есть Точка имеет специальное имя. Это называется происхождением.
Происхождение
Точка называется началом координат . Это точка пересечения осей x и y .
Это точка пересечения осей x и y .
Мы используем координаты, чтобы найти точку на плоскости xy .Давайте нарисуем точку в качестве примера. Во-первых, найдите 1 на оси x и слегка нарисуйте вертикальную линию, проходящую через нее. Затем найдите 3 на оси y и нарисуйте горизонтальную линию, проходящую через нее. Теперь найдите точку, где эти две линии встречаются — это точка. с координатами См. (рисунок).
Обратите внимание, что сквозная вертикальная линия и горизонтальная линия не являются частью графика. Мы просто использовали их, чтобы помочь нам найти точку
.Когда одна из координат равна нулю, точка лежит на одной из осей.На (рисунке) точка находится на оси y , а точка на оси x .
Точки на осях
Точки с координатой y , равной 0, находятся на оси x и имеют координаты
Точки с координатой x , равной 0, находятся на оси y и имеют координаты
Знаки координаты x и координаты y влияют на расположение точек.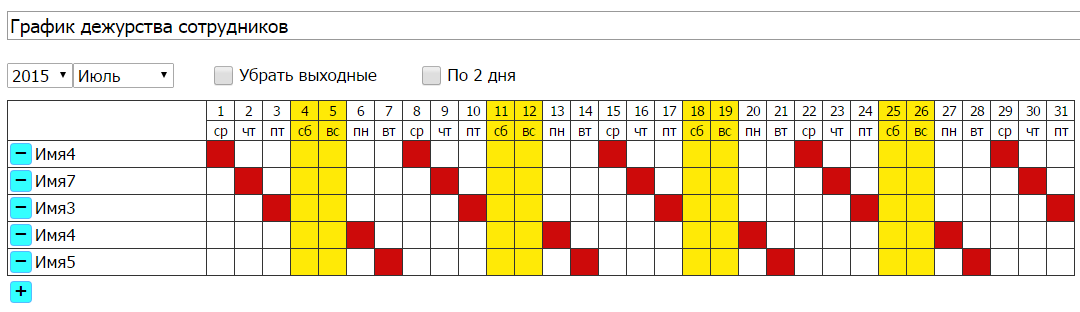 Возможно, вы заметили некоторые закономерности, когда рисовали точки в предыдущем примере. Мы можем обобщить знаковые паттерны квадрантов следующим образом:
Возможно, вы заметили некоторые закономерности, когда рисовали точки в предыдущем примере. Мы можем обобщить знаковые паттерны квадрантов следующим образом:
Квадранты
До сих пор все уравнения, которые вы решали, были уравнениями с одной переменной. Почти в каждом случае, когда вы решали уравнение, вы получали ровно одно решение. Но уравнения могут иметь более одной переменной. Уравнения с двумя переменными могут быть вида Уравнение такого вида называется линейным уравнением с двумя переменными.
Линейное уравнение
Уравнение вида, где A и B не равны нулю, называется линейным уравнением с двумя переменными.
Вот пример линейного уравнения с двумя переменными, x и y .
Уравнение также является линейным уравнением. Но это не похоже на форму. Мы можем использовать свойство сложения равенства и переписать его в форме.
Переписав, как мы можем легко увидеть, что это линейное уравнение с двумя переменными, потому что оно имеет форму Когда уравнение имеет форму, мы говорим, что оно находится в стандартной форме линейного уравнения.
Стандартная форма линейного уравнения
Линейное уравнение имеет стандартную форму при записи
Большинство людей предпочитают, чтобы A , B и C были целыми числами при написании линейного уравнения в стандартной форме, хотя это не является строго необходимым.
Линейные уравнения имеют бесконечно много решений. Для каждого числа, которое заменяется на x , есть соответствующее значение y .Эта пара значений является решением линейного уравнения и представлена упорядоченной парой. Когда мы подставляем эти значения x и y в уравнение, результат является верным утверждением, потому что значение в левой части равно равно значению в правой части.
Решение линейного уравнения с двумя переменными
Упорядоченная пара является решением линейного уравнения, если уравнение является истинным утверждением, когда значения x – и y упорядоченной пары подставлены в уравнение.
Линейные уравнения имеют бесконечно много решений. Мы можем построить эти решения в прямоугольной системе координат. Точки идеально совпадут по прямой линии. Соединяем точки прямой линией, чтобы получить график уравнения. Мы помещаем стрелки на концы каждой стороны линии, чтобы указать, что линия продолжается в обоих направлениях.
График — это визуальное представление всех решений уравнения. Это пример поговорки: «Картинка стоит тысячи слов.Строка показывает вам всех решений этого уравнения. Каждая точка на прямой является решением уравнения. И каждое решение этого уравнения находится на этой прямой.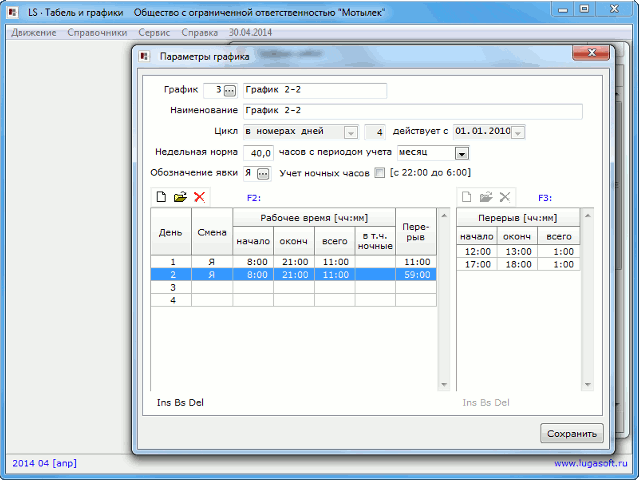 Эта линия называется графиком уравнения. Точки , а не на прямой не являются решениями!
Эта линия называется графиком уравнения. Точки , а не на прямой не являются решениями!
График линейного уравнения
График линейного уравнения представляет собой прямую линию.
- Каждая точка на прямой является решением уравнения.
- Каждое решение этого уравнения является точкой на этой прямой.
Показан график.
Для каждой заказанной пары решить:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Точка на линии?
А: Б: В: Г:
Подставьте значения x – и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
ⓐ
ⓑ Нанесите точки и
Точки и находятся на прямой, а точка не на прямой.
Точки, являющиеся решениями, находятся на прямой, но точка, не являющаяся решением, не находится на прямой.
Использовать график Для каждой заказанной пары решить:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Точка на линии?
А Б
ⓐ да, да ⓑ да, да
Использовать график Для каждой заказанной пары решить:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Точка на линии?
А Б
График линейного уравнения по точкам
Существует несколько методов построения графика линейного уравнения.Первый метод, который мы будем использовать, называется построением точек или методом построения точек. Мы находим три точки, координаты которых являются решениями уравнения, и затем наносим их в прямоугольную систему координат. Соединив эти точки линией, мы получим график линейного уравнения.
Как построить график линейного уравнения по точкам
Нарисуйте график уравнения, нанеся точки.
График уравнения по точкам:
График уравнения по точкам:
Шаги, которые нужно предпринять при построении графика линейного уравнения с помощью точек, приведены здесь.
Построить график линейного уравнения по точкам.
- Найдите три точки, координаты которых являются решениями уравнения. Организуйте их в виде таблицы.
- Нанесите точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если их нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Расширьте линию, чтобы заполнить сетку, и поставьте стрелки на обоих концах линии.
Это правда, что для определения линии требуется всего две точки, но использование трех точек является хорошей привычкой.Если вы нанесете только две точки, и одна из них неверна, вы все равно сможете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверная, точки не выстроятся. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите, чем отличаются эти иллюстрации.
Когда уравнение включает дробь в качестве коэффициента , мы все еще можем заменить x любыми числами.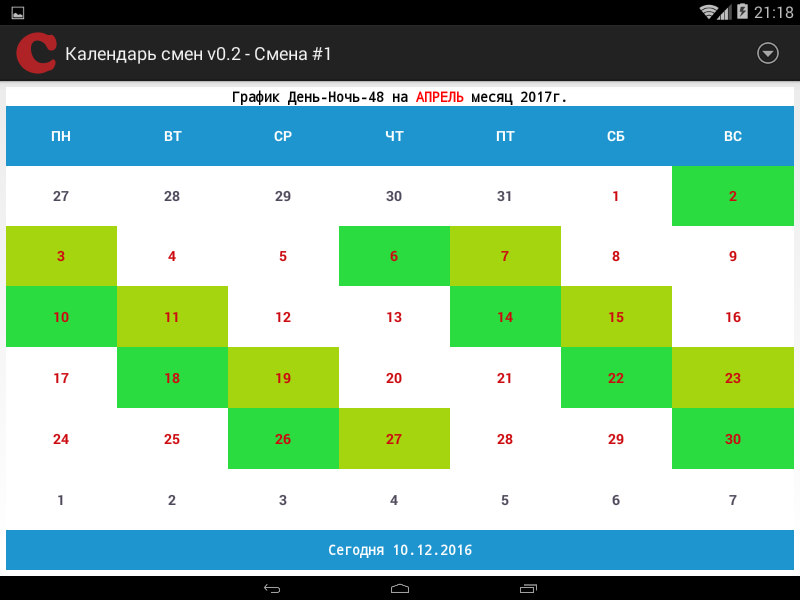 Но арифметика упрощается, если мы делаем «хороший» выбор для значений x . Таким образом, мы избежим дробных ответов, которые трудно точно изобразить в виде графика.
Но арифметика упрощается, если мы делаем «хороший» выбор для значений x . Таким образом, мы избежим дробных ответов, которые трудно точно изобразить в виде графика.
Нарисуйте уравнение:
Найдите три точки, являющиеся решениями уравнения. Поскольку в этом уравнении дробь имеет коэффициент x , мы будем тщательно выбирать значения x . Мы будем использовать ноль в качестве одного варианта и числа, кратные 2, для других вариантов. Почему числа, кратные двум, являются хорошим выбором для значений x ? При выборе числа, кратного 2, умножение упрощается до целого числа
.Точки показаны на (Рисунок).
Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию.
Нарисуйте уравнение:
Нарисуйте уравнение:
График вертикальных и горизонтальных линий
Некоторые линейные уравнения имеют только одну переменную.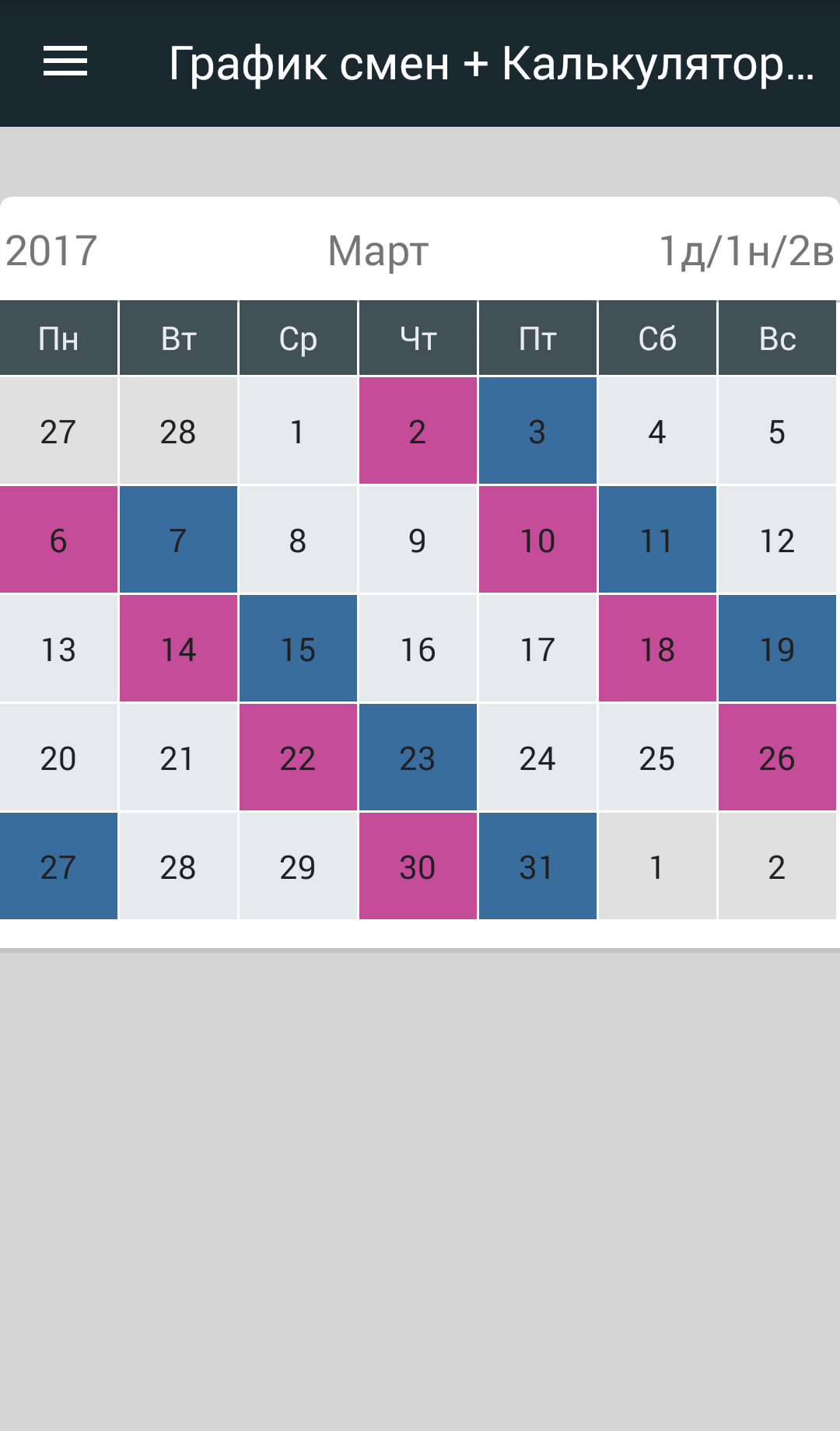 Они могут иметь только x и не иметь y , или только y без x . Это меняет то, как мы делаем таблицу значений, чтобы получить точки для построения.
Они могут иметь только x и не иметь y , или только y без x . Это меняет то, как мы делаем таблицу значений, чтобы получить точки для построения.
Давайте рассмотрим уравнение. Это уравнение имеет только одну переменную, x . Уравнение говорит, что x равно , всегда равно, поэтому его значение не зависит от y . Независимо от того, каково значение y , значение x всегда равно
. Итак, чтобы составить таблицу значений, запишите все значения x . Затем выберите любые значения для y . Поскольку x не зависит от y , вы можете выбрать любые числа. Но чтобы разместить точки на нашем графике координат, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Но чтобы разместить точки на нашем графике координат, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Нанесите точки из таблицы и соедините их прямой линией. Обратите внимание, что мы начертили вертикальную линию.
Что, если в уравнении есть х , но нет х ? Давайте нарисуем уравнение. На этот раз значение y- является константой, поэтому в этом уравнении y не зависит от x . Введите 4 для всех y на (Рисунок), а затем выберите любые значения для x .Мы будем использовать 0, 2 и 4 для координат x .
На этом рисунке мы изобразили горизонтальную линию, проходящую через ось y в точке 4.
График: ⓐ ⓑ
ⓐ Уравнение имеет только одну переменную, x , а x всегда равно 2. Мы создаем таблицу, в которой x всегда равно 2, а затем вводим любые значения для y . График представляет собой вертикальную линию, проходящую через ось x в точке 2.
Мы создаем таблицу, в которой x всегда равно 2, а затем вводим любые значения для y . График представляет собой вертикальную линию, проходящую через ось x в точке 2.
ⓑ Точно так же уравнение имеет только одну переменную, y . Значение y является постоянным. Все упорядоченные пары в следующей таблице имеют одну и ту же координату y . График представляет собой горизонтальную линию, проходящую через ось y в точке
.Нарисуйте уравнения: ⓐ ⓑ
ⓐ
ⓑ
Нарисуйте уравнения: ⓐ ⓑ
ⓐ
ⓑ
В чем разница между уравнениями и
Уравнение имеет как x , так и y . Значение y зависит от значения x , поэтому координата y изменяется в соответствии со значением x . Уравнение имеет только одну переменную. Значение y является постоянным, оно не зависит от значения x , поэтому координата y всегда равна 4.
Значение y зависит от значения x , поэтому координата y изменяется в соответствии со значением x . Уравнение имеет только одну переменную. Значение y является постоянным, оно не зависит от значения x , поэтому координата y всегда равна 4.
Обратите внимание, что на графике уравнение представляет собой наклонную линию, а горизонтальную линию.
График и в той же прямоугольной системе координат.
Заметим, что в первом уравнении есть переменная x , а во втором нет. Мы делаем таблицу точек для каждого уравнения, а затем рисуем линии. Показаны два графика.
Нарисуйте уравнения в той же прямоугольной системе координат: и
Нарисуйте уравнения в той же прямоугольной системе координат: и
Найти
x – и y – перехваты Каждое линейное уравнение может быть представлено уникальной линией, показывающей все решения уравнения. Мы видели, что при построении графика с помощью точек можно использовать любые три решения для построения графика. Это означает, что два человека, рисующие линию, могут использовать разные наборы из трех точек.
Мы видели, что при построении графика с помощью точек можно использовать любые три решения для построения графика. Это означает, что два человека, рисующие линию, могут использовать разные наборы из трех точек.
На первый взгляд две их линии могут показаться неодинаковыми, так как они будут иметь разные точки. Но если вся работа была проделана правильно, линии должны получиться точно такими же. Один из способов узнать, что это действительно одна и та же линия, — посмотреть, где линия пересекает оси x и оси y .Эти точки называются точками пересечения прямой.
Пересечение линии
Точки пересечения линией оси x и оси y называются точками пересечения линии .
Давайте посмотрим на графики линий.
Во-первых, обратите внимание, где каждая из этих линий пересекает ось x . См. (Рисунок).
См. (Рисунок).
Теперь давайте посмотрим на точки, где эти линии пересекают ось y .
ось x в точке: Заказанная пара
для этой точки Линия пересекает
ось y- в точке: Заказанная пара
для этой точки Рис. )5Рисунок (d)00Общий рисунок a b
Вы видите закономерность?
Для каждой линии координата y точки, в которой линия пересекает ось x , равна нулю. Точка, в которой линия пересекает ось x , имеет форму и называется точкой пересечения x линии.Перехват x происходит, когда y равно нулю.
В каждой строке координата x – точки, где линия пересекает ось y , равна нулю. Точка, в которой линия пересекает ось y , имеет форму и называется точкой пересечения y линии. Перехват y происходит, когда x равно нулю.
x -пересечение и y -пересечение линии
Точка пересечения x – это точка, в которой линия пересекает ось x .
Точка пересечения y – это точка пересечения прямой с осью y .
Найдите точки пересечения x и y на каждом показанном графике.
ⓐ График пересекает ось x в точке Точка пересечения x составляет
График пересекает ось y в точке Точка пересечения y равна
ⓑ График пересекает ось x в точке.
График пересекает ось y в точке Точка пересечения y равна
ⓒ График пересекает ось x в точке.
График пересекает ось y в точке Точка пересечения y равна
Найдите точки пересечения x – и y на графике.
x -пересечение:
г -перехват:
Найдите точки пересечения x – и y на графике.
x -пересечение:
г -перехват:
Признание того, что пересечение x происходит, когда y равно нулю, и что пересечение y происходит, когда x равно нулю, дает нам метод нахождения пересечений линии из ее уравнения.Чтобы найти x -перехват, пусть и решить для x . Чтобы найти y -перехват, пусть и решить для y .
Найдите точки пересечения x и y из уравнения прямой
Используйте уравнение линии. Найти:
- х -пересечение линии, пусть и решает для х .

- y -пересечение линии, пусть и решить для y .
Найти пересечения
Позволим найти x -перехват, и позволим найти y -перехват.Мы заполним таблицу, которая напоминает нам о том, что нам нужно найти.
Точки пересечения – это точки и как показано в таблице.
| х | у |
| 4 | 0 |
| 0 | 8 |
Найти перехваты:
x -пересечение:
г -перехват:
Найти перехваты:
x -пересечение:
г -перехват:
Нарисуйте линию, используя точки пересечения
Чтобы построить линейное уравнение по точкам, вам нужно найти три точки, координаты которых являются решениями уравнения. Вы можете использовать точки пересечения x- и y- как две из трех ваших точек. Найдите пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают, затем нарисуйте линию. Этот метод часто является самым быстрым способом построения графика.
Вы можете использовать точки пересечения x- и y- как две из трех ваших точек. Найдите пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают, затем нарисуйте линию. Этот метод часто является самым быстрым способом построения графика.
Как построить линию с помощью точек пересечения
График с использованием перехватов.
График с использованием точек пересечения:
График с использованием точек пересечения:
Шаги построения графика линейного уравнения с использованием точек пересечения приведены здесь.
Постройте линейное уравнение, используя точки пересечения.
- Найдите x – и y – точки пересечения линии.
- Пусть и решить для x .
- Пусть и решить для y .

- Найдите третье решение уравнения.
- Нанесите три точки и убедитесь, что они совпадают.
- Нарисуй линию.
График с использованием перехватов.
Найдите точки пересечения и третью точку.
Перечислим точки в таблице и покажем график.
График с использованием точек пересечения:
График с использованием точек пересечения:
Когда линия проходит через начало координат, точка пересечения x и точка пересечения y являются одной и той же точкой.
График с использованием перехватов.
В этой строке есть только один отрезок. Это точка
Для обеспечения точности нам нужно нанести три точки.Поскольку точки пересечения x и y являются одной и той же точкой, нам нужно еще две точек, чтобы построить линию.
Полученные три точки сведены в таблицу.
Нанесите три точки, убедитесь, что они совпадают, и начертите линию.
График с использованием точек пересечения:
График пересечений:
Практика делает совершенным
Точки графика в прямоугольной системе координат
В следующих упражнениях постройте каждую точку в прямоугольной системе координат и определите квадрант, в котором она расположена.
В следующих упражнениях для каждой заказанной пары определите
ⓐ является ли упорядоченная пара решением уравнения? ⓑ это точка на линии?
ⓐ A: да, B: нет, C: да, D: да ⓑ A: да, B: нет, C: да, D: да
ⓐ A: да, B: да, C: да, D: нет ⓑ A: да, B: да, C: да, D: нет
График линейного уравнения по точкам
В следующих упражнениях постройте график по точкам.
Вертикальные и горизонтальные линии графика
В следующих упражнениях постройте график каждого уравнения.
ⓐⓑ
ⓐⓑ
В следующих упражнениях постройте график каждой пары уравнений в одной и той же прямоугольной системе координат.
и
и
Найти x- и y- Перехваты
В следующих упражнениях найдите точки пересечения x и y на каждом графике.
В следующих упражнениях найдите точки пересечения для каждого уравнения.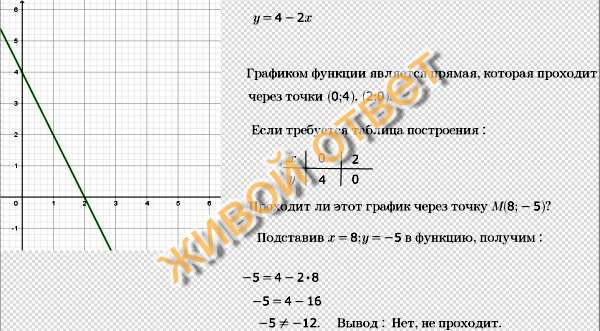
Построить линию с использованием точек пересечения
В следующих упражнениях постройте график, используя точки пересечения.
Смешанная практика
В следующих упражнениях постройте график каждого уравнения.
Письменные упражнения
Объясните, как выбрать три значения x , чтобы составить таблицу для построения графика линии
В чем разница между уравнениями вертикальной и горизонтальной прямой?
Вы предпочитаете использовать метод построения точек или метод с использованием точек пересечения для построения графика уравнения Почему?
Вы предпочитаете использовать метод построения точек или метод с использованием точек пересечения для построения графика уравнения Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Если большинство ваших чеков было:
Уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретными.
С некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа.Кого можно попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
Нет, не понимаю. Это предупреждающий знак, и вы должны принять меры. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Вместе вы можете придумать план, как получить необходимую вам помощь.
графических навыков: четвертый блок
графических навыков: четвертый блокРасчет уклона
Чтобы вычислить наклон линии, вам нужно всего две точки из эта строка, ( x 1, y 1) и ( x 2, y 2).
| Уравнение, используемое для расчета уклона по двум точкам: | На графике это можно представить как: |
Существует три этапа вычисления наклона прямой. линия, когда вам не дано ее уравнение.
- Шаг первый: Определите две точки на прямой.
- Шаг второй: Выберите один из них ( x 1, y 1)
а другой должен быть ( x 2, y 2).

- Шаг третий: Используйте уравнение наклона для расчета уклона.
Найдите минутку, чтобы проработать пример, в котором нам дается две точки.
Пример
Допустим, точки (15, 8) и (10, 7) лежат на прямой. Каков наклон этой линии?
- Шаг первый: Определите две точки на прямой.
В этом примере нам даны две точки, (15, 8) и (10, 7), по прямой.
- Шаг второй: Выберите один из них ( x 1, y 1)
а другой должен быть ( x 2, y 2).
Неважно, что мы выберем, так что пусть (15, 8) будет ( х 2, у 2). Возьмем точку (10, 7) быть точкой ( х 1, и 1).
- Шаг третий: Используйте уравнение для расчета уклона.
После того, как мы завершили шаг 2, мы готовы вычислить наклон используя уравнение для наклона:
Мы сказали, что на самом деле не имеет значения, какую точку мы выберем как ( x 1, y 1) и каким быть ( x 2, y 2).
 Покажем, что это правда. Возьмите те же две точки (15, 8)
и (10, 7), но на этот раз мы будем вычислять наклон, используя (15,
8) как ( x 1, y 1) и (10, 7) как точка ( x 2, y 2).Затем подставьте их в уравнение для наклона:
Покажем, что это правда. Возьмите те же две точки (15, 8)
и (10, 7), но на этот раз мы будем вычислять наклон, используя (15,
8) как ( x 1, y 1) и (10, 7) как точка ( x 2, y 2).Затем подставьте их в уравнение для наклона:Получаем тот же ответ, что и раньше!
Часто вам не дадут два очка, но вам нужно будет определить две точки на графике. В этом случае процесс то же самое, первым шагом является определение точек из график. Ниже приведен пример, который начинается с графика.
Пример
| Каков наклон линии, изображенной на графике? Наклон этой линии равен 2. |
[подробное решение к примеру]
Теперь найдите минутку и сравните две линии на тот же график.
Обратите внимание, что линия с большим наклоном является более крутой из
два. |
Теперь вы готовы решить практическую задачу. Если вы уже выполнили первую практическую задачу для этого модуля, который вы можете пожелать попробовать дополнительную практику.
4.2 График линейных уравнений с двумя переменными — Элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решить задачи с монетами
- Решение задач с билетами и штампами
- Решить задачи на смешанные слова
- Использование смешанной модели для решения инвестиционных задач с использованием простых процентов
Будьте готовы 4. 4
4
Прежде чем начать, пройдите этот тест на готовность.
Вычислите 3x+23x+2, когда x=−1x=−1.
Если вы пропустили эту проблему, просмотрите пример 1.57.
Будьте готовы 4.5
Решите 3x+2y=123x+2y=12 для yy в целом.
Если вы пропустили эту проблему, просмотрите пример 2.63.
Распознать взаимосвязь между решениями уравнения и его графиком
В предыдущем разделе мы нашли несколько решений уравнения 3x+2y=63x+2y=6.Они перечислены в таблице 4.10. Итак, упорядоченные пары (0,3)(0,3), (2,0)(2,0) и (1,32)(1,32) являются решениями уравнения 3x+2y=63x+ 2у=6. Мы можем построить эти решения в прямоугольной системе координат, как показано на рис. 4.5.
| 3x+2y=63x+2y=6 | ||
| хх | г. г. г. | (х, у) (х, у) |
| 0 | 3 | (0,3)(0,3) |
| 2 | 0 | (2,0)(2,0) |
| 1 | 3232 | (1,32)(1,32) |
Таблица 4.10
Рисунок 4.5
Заметили, что точки идеально совпадают? Соединяем точки линией, чтобы получить график уравнения 3x+2y=63x+2y=6. См. рис. 4.6. Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают, что линия продолжается.
Рисунок 4.6
Каждая точка на прямой является решением уравнения. Кроме того, каждое решение этого уравнения является точкой на этой прямой. Точки , а не на прямой не являются решениями.
Обратите внимание, что точка с координатами (−2,6)(−2,6) находится на линии, показанной на рис. 4.7. Если вы подставите x=-2x=-2 и y=6y=6 в уравнение, вы обнаружите, что это решение уравнения.
Рисунок 4.7
Итак, точка (−2,6)(−2,6) является решением уравнения 3x+2y=63x+2y=6. (Фраза «точка с координатами (−2,6)(−2,6)» часто сокращается до «точка (−2,6)(−2,6)».)
Итак, (4,1)(4,1) не является решением уравнения 3x+2y=63x+2y=6.Следовательно, точка (4,1)(4,1) не лежит на прямой. См. рис. 4.6. Это пример поговорки: «Картинка стоит тысячи слов». Строка показывает вам всех решений уравнения. Каждая точка на прямой является решением уравнения. И каждое решение этого уравнения находится на этой прямой.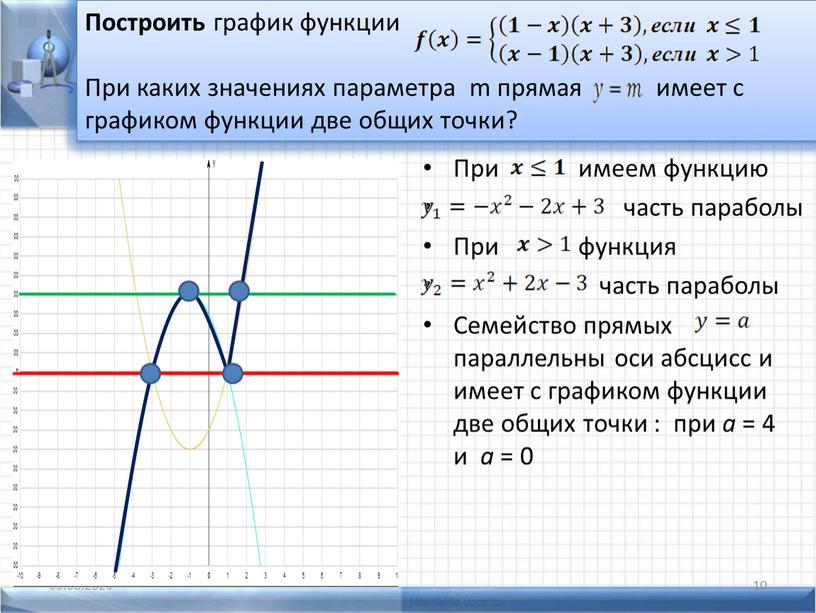 Эта линия называется графиком уравнения 3x+2y=63x+2y=6.
Эта линия называется графиком уравнения 3x+2y=63x+2y=6.
График линейного уравнения
График линейного уравнения Ax+By=CAx+By=C представляет собой прямую.
- Каждая точка на прямой является решением уравнения.
- Каждое решение этого уравнения является точкой на этой прямой.
Пример 4.10
Показан график y=2x−3y=2x−3.
Для каждой заказанной пары решить:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Точка на линии?
A (0,−3)(0,−3) B (3,3)(3,3) C (2,−3)(2,−3) D (−1,−5)(−1, −5)
Решение
Подставьте значения x – и y – в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
- ⓐ
- ⓑ Нанесите точки A (0,3)(0,3), B (3,3)(3,3), C (2,−3)(2,−3) и D (−1,− 5)(−1,−5).

Точки (0,3)(0,3), (3,3)(3,3) и (−1,−5)(−1,−5) лежат на прямой y=2x−3y =2x−3, а точка (2,−3)(2,−3) не лежит на прямой.
Точки, являющиеся решениями y=2x−3y=2x−3, находятся на прямой, но точка, не являющаяся решением, не находится на прямой.
Попробуйте 4.19
Используйте график y=3x−1y=3x−1, чтобы решить, является ли каждая упорядоченная пара:
- решение уравнения.
- на линии.
ⓐ (0,−1)(0,−1) ⓑ (2,5)(2,5)
Попробуйте 4.20
Используйте график y=3x−1y=3x−1, чтобы решить, является ли каждая упорядоченная пара:
- решение уравнения
- на линии
ⓐ (3,−1)(3,−1) ⓑ (−1,−4)(−1,−4)
График линейного уравнения по точкам
Существует несколько методов построения графика линейного уравнения. Метод, который мы использовали для построения графика 3x+2y=63x+2y=6, называется построением точек или методом построения точек.
Пример 4.11
Как построить уравнение по точкам
Нарисуйте график уравнения y=2x+1y=2x+1, нанеся точки.
Попробуйте 4.21
Нарисуйте уравнение, нанеся точки: y=2x−3y=2x−3.
Попробуйте 4.22
Нарисуйте уравнение, нанеся точки: y=−2x+4y=−2x+4.
Шаги, которые необходимо предпринять при построении графика линейного уравнения с помощью точек, приведены ниже.
How To
Постройте график линейного уравнения, нанеся точки.
- Шаг 1. Найдите три точки, координаты которых являются решениями уравнения. Организуйте их в виде таблицы.
- Шаг 2. Нанесите точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если их нет, внимательно проверьте свою работу.
- Шаг 3. Проведите линию через три точки. Расширьте линию, чтобы заполнить сетку, и поставьте стрелки на обоих концах линии.
Это правда, что для определения линии требуется всего две точки, но использование трех точек является хорошей привычкой. Если вы нанесете только две точки, и одна из них неверна, вы все равно сможете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы нанесете только две точки, и одна из них неверна, вы все равно сможете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверная, точки не выстроятся. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (а) и частью (б) на рис. 4.8.
Рисунок 4.8
Давайте сделаем еще один пример. На этот раз мы покажем последние два шага на одной сетке.
Пример 4.12
Нарисуйте график уравнения y=−3xy=−3x.
Решение
Найдите три точки, являющиеся решениями уравнения. Здесь, опять же, проще выбрать значения для xx. Вы понимаете, почему?
Перечислим точки в таблице 4.11.
| y=-3xy=-3x | ||
| хх | г. г. г. | (х, у) (х, у) |
| 0 | 0 | (0,0)(0,0) |
| 1 | −3−3 | (1,−3)(1,−3) |
| −2−2 | 6 | (−2,6)(−2,6) |
Таблица 4.11
Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию.
Попробуйте 4.23
Нарисуйте уравнение, нанеся точки: y=−4xy=−4x.
Попробуйте 4.24
Нарисуйте уравнение, нанеся точки: y=xy=x.
Когда уравнение включает дробь в качестве коэффициента xx, мы все равно можем заменить xx любыми числами. Но математика упрощается, если мы делаем «хороший» выбор значений xx. Таким образом, мы избежим дробных ответов, которые трудно точно изобразить в виде графика.
Пример 4.13
Нарисуйте график уравнения y=12x+3y=12x+3.
Решение
Найдите три точки, являющиеся решениями уравнения. Поскольку это уравнение имеет дробь 1212 в качестве коэффициента x,x, мы будем тщательно выбирать значения xx. Мы будем использовать ноль в качестве одного варианта и числа, кратные 2, для других вариантов. Почему числа, кратные 2, являются хорошим выбором для значений xx?
Точки показаны в таблице 4.12.
| у=12х+3у=12х+3 | ||
| хх | г. г. г. | (х, у) (х, у) |
| 0 | 3 | (0,3)(0,3) |
| 2 | 4 | (2,4)(2,4) |
| 4 | 5 | (4,5)(4,5) |
Таблица 4.12
Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию.
Попробуйте 4.25
Нарисуйте график уравнения y=13x−1y=13x−1.
Попробуйте 4.26
Нарисуйте график уравнения y=14x+2y=14x+2.
До сих пор во всех уравнениях, которые мы рисовали, yy выражалось через xx. Теперь мы нарисуем уравнение с xx и yy на одной стороне. Давайте посмотрим, что происходит в уравнении 2x+y=32x+y=3. Если y=0y=0, каково значение xx?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем изобразить эту точку на графике, трудно изобразить точные дроби.Помните, что в примере y=12x+3y=12x+3 мы тщательно выбирали значения для xx, чтобы вообще не отображать дроби. Если мы решим уравнение 2x+y=32x+y=3 относительно yy, будет легче найти три решения уравнения.
2х+у=3у=-2х+32х+у=3у=-2х+3Решения для x=0x=0, x=1x=1 и x=-1x=-1 показаны в таблице 4.13. График показан на рис. 4.9.
| 2x+y=32x+y=3 | ||
| хх | г. г. г. | (х, у) (х, у) |
| 0 | 3 | (0,3)(0,3) |
| 1 | 1 | (1,1)(1,1) |
| −1−1 | 5 | (−1,5)(−1,5) |
Таблица 4.13
Рисунок 4.9
Можете ли вы найти на прямой точку (32,0)(32,0), которую мы нашли, полагая y=0y=0?
Пример 4.14
Нарисуйте уравнение 3x+y=−13x+y=−1.
Решение
Таблица 4.14
Пусть xx будет 0, 1 и −1−1, чтобы найти 3 точки. Упорядоченные пары показаны в таблице 4.15. Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию. См. Рисунок 4.10.
| 3x+y=-13x+y=-1 | ||
| хх | г.г. | (х, у) (х, у) |
| 0 | −1−1 | (0,−1)(0,−1) |
| 1 | −4−4 | (1,−4)(1,−4) |
| −1−1 | 2 | (−1,2)(−1,2) |
Таблица 4. 15
15
Рисунок 4.10
Попробуйте 4.27
Нарисуйте уравнение 2x+y=22x+y=2.
Попробуйте 4.28
Нарисуйте график уравнения 4x+y=−34x+y=−3.
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, соответствует ли ваш график графику, показанному в ответах в книге? Если точки, в которых графики пересекают оси x и y , совпадают, графики совпадают!
Уравнение в примере 4.14 было записано в стандартной форме, где xx и yy находятся на одной стороне.Мы решили это уравнение для yy всего за один шаг. Но для других уравнений в стандартной форме решить относительно yy не так просто, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения, если x=0x=0 и найти yy. Мы можем построить вторую точку, положив y=0y=0, а затем найдя xx. Затем мы нанесем третью точку, используя другое значение для xx или yy.
Пример 4.
 15
15Нарисуйте уравнение 2x−3y=62x−3y=6.
Решение
| Найдите три точки, являющиеся решениями уравнения. | 2x−3y=62x−3y=6 |
| Сначала пусть x=0x=0. | 2(0)−3y=62(0)−3y=6 |
| Решите для гг. | −3y=6y=−2−3y=6y=−2 |
| Теперь пусть y=0y=0. | 2x−3(0)=62x−3(0)=6 |
| Решите для xx. | 2х=6х=32х=6х=3 |
| Нам нужна третья точка. Помните, мы можем выбрать любое значение для xx или yy. Допустим, х=6х=6. | 2(6)−3y=62(6)−3y=6 |
| Решите для гг. | 12−3y=6−3y=−6y=212−3y=6−3y=−6y=2 |
Таблица 4.16
Мы перечисляем упорядоченные пары в таблице 4.17. Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию. См. Рисунок 4.11.
| 2x−3y=62x−3y=6 | ||
| хх | г.г. | (х, у) (х, у) |
| 0 | −2−2 | (0,−2)(0,−2) |
| 3 | 0 | (3,0)(3,0) |
| 6 | 2 | (6,2)(6,2) |
Таблица 4.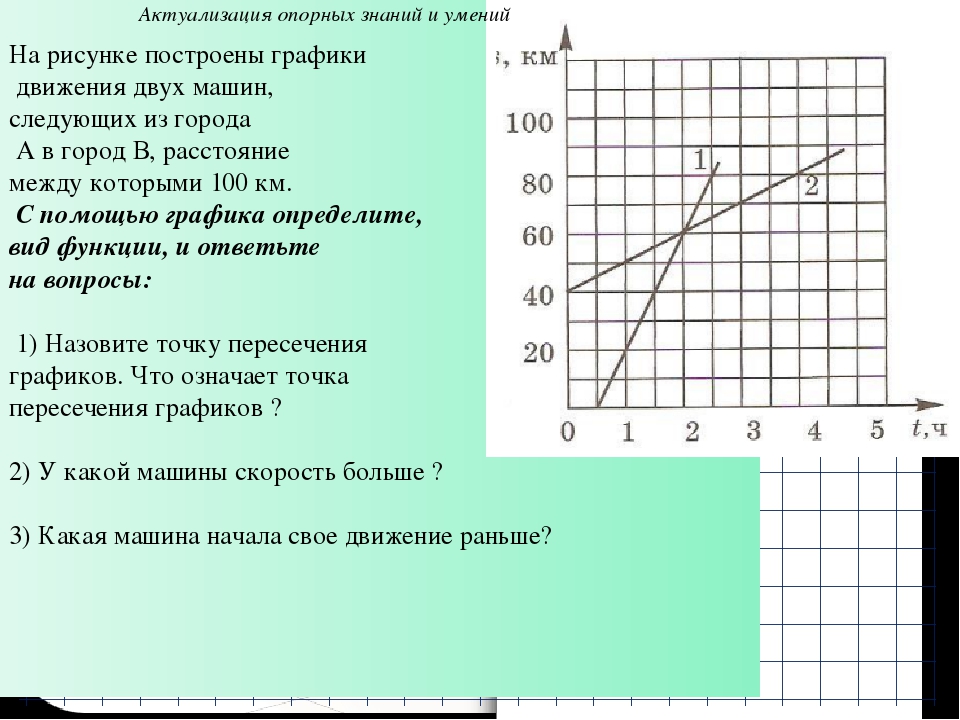 17
17
Рисунок 4.11
Попробуйте 4.29
Нарисуйте уравнение 4x+2y=84x+2y=8.
Попробуйте 4.30
Нарисуйте уравнение 2x−4y=82x−4y=8.
График вертикальных и горизонтальных линий
Можем ли мы построить уравнение только с одной переменной? Просто xx и без yy, или просто yy без xx? Как мы составим таблицу значений, чтобы получить точки для построения?
Рассмотрим уравнение x=−3x=−3. Это уравнение имеет только одну переменную xx.Уравнение говорит, что xx равно , всегда равно −3−3, поэтому его значение не зависит от yy. Независимо от того, что такое yy, значение xx всегда равно −3−3.
Итак, чтобы составить таблицу значений, запишите -3−3 in для всех значений xx. Затем выберите любые значения для yy. Поскольку xx не зависит от yy, вы можете выбрать любые числа. Но чтобы разместить точки на нашем графике координат, мы будем использовать 1, 2 и 3 для координат y . См. Таблицу 4.18.
См. Таблицу 4.18.
| х=-3х=-3 | ||
| хх | г.г. | (х, у) (х, у) |
| −3−3 | 1 | (−3,1)(−3,1) |
| −3−3 | 2 | (−3,2)(−3,2) |
| −3−3 | 3 | (−3,3)(−3,3) |
Таблица 4. 18
18
Нанесите точки из Таблицы 4.18 и соедините их прямой линией. Обратите внимание, что на рис. 4.12 мы начертили вертикальную линию .
Рисунок 4.12
Вертикальная линия
Вертикальная линия — это график уравнения вида x=ax=a.
Линия проходит через ось x в точке (a,0)(a,0).
Пример 4.16
Нарисуйте уравнение x=2x=2.
Решение
Уравнение имеет только одну переменную, xx, и xx всегда равно 2.Мы создаем Таблицу 4.19, где xx всегда равно 2, а затем вставляем любые значения для yy. График представляет собой вертикальную линию, проходящую через ось x в точке 2. См. рис. 4.13.
| х=2х=2 | ||
| хх | г. г. г. | (х, у) (х, у) |
| 2 | 1 | (2,1)(2,1) |
| 2 | 2 | (2,2)(2,2) |
| 2 | 3 | (2,3)(2,3) |
Таблица 4.19
Рисунок 4.13
Попробуйте 4.31
Нарисуйте график уравнения x=5x=5.
Попробуйте 4.32
Нарисуйте график уравнения x=−2x=−2.
Что делать, если в уравнении есть yy, но нет xx? Нарисуем уравнение y=4y=4. На этот раз значение y – является константой, поэтому в этом уравнении yy не зависит от xx. Заполните 4 для всех yy в таблице 4.20, а затем выберите любые значения для xx. Мы будем использовать 0, 2 и 4 для координат x .
На этот раз значение y – является константой, поэтому в этом уравнении yy не зависит от xx. Заполните 4 для всех yy в таблице 4.20, а затем выберите любые значения для xx. Мы будем использовать 0, 2 и 4 для координат x .
| у=4у=4 | ||
| хх | г.г. | (х, у) (х, у) |
| 0 | 4 | (0,4)(0,4) |
| 2 | 4 | (2,4)(2,4) |
| 4 | 4 | (4,4)(4,4) |
Таблица 4.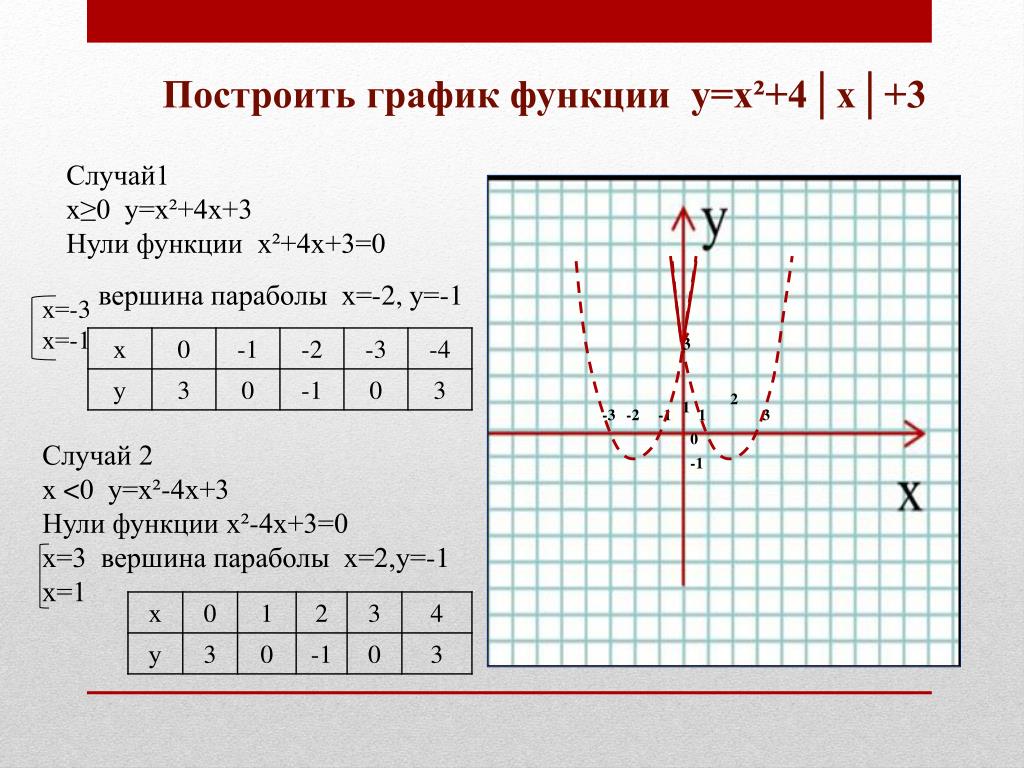 20
20
График представляет собой горизонтальную линию, проходящую через ось y в точке 4.См. Рисунок 4.14.
Рисунок 4.14
Горизонтальная линия
Горизонтальная линия — это график уравнения вида y=by=b.
Линия проходит через ось y в точке (0,b)(0,b).
Пример 4.17
Нарисуйте график уравнения y=−1.y=−1.
Решение
Уравнение y=−1y=−1 имеет только одну переменную yy. Значение yy является постоянным. Все упорядоченные пары в таблице 4.21 имеют одну и ту же координату y .График представляет собой горизонтальную линию, проходящую через ось y в точке −1−1, как показано на рисунке 4.15.
| у=-1у=-1 | ||
| хх | г. г. г. | (х, у) (х, у) |
| 0 | −1−1 | (0,−1)(0,−1) |
| 3 | −1−1 | (3,−1)(3,−1) |
| −3−3 | −1−1 | (-3,-1)(-3,-1) |
Таблица 4.21
Рисунок 4.15
Попробуйте 4.33
Нарисуйте график уравнения y=−4y=−4.
Попробуйте 4.34
Нарисуйте график уравнения y=3y=3.
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа y=4x.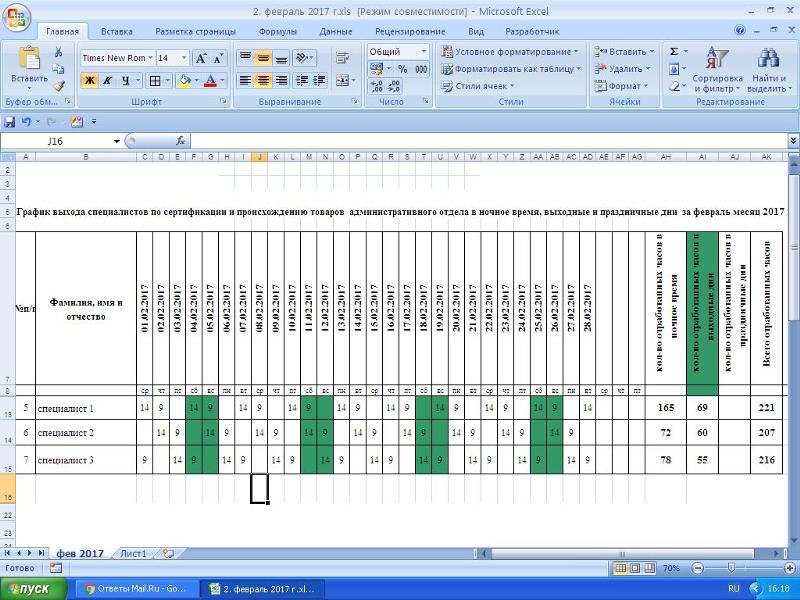 y=4x. В чем разница между уравнениями y=4xy=4x и y=4y=4?
y=4x. В чем разница между уравнениями y=4xy=4x и y=4y=4?
Уравнение y=4xy=4x имеет как xx, так и yy. Значение yy зависит от значения xx. Координата y изменяется в соответствии со значением xx.Уравнение y=4y=4 имеет только одну переменную. Значение yy является постоянным. Координата y всегда равна 4. Она не зависит от значения xx. См. Таблицу 4.22.
| у=4ху=4х | у=4у=4 | |||||
| хх | г.г. | (х, у) (х, у) | хх | г.г. | (х, у) (х, у) | |
| 0 | 0 | (0,0)(0,0) | 0 | 4 | (0,4)(0,4) | |
| 1 | 4 | (1,4)(1,4) | 1 | 4 | (1,4)(1,4) | |
| 2 | 8 | (2,8)(2,8) | 2 | 4 | (2,4)(2,4) | |
Таблица 4.22
Рисунок 4.16
Обратите внимание, что на рис. 4.16 уравнение y=4xy=4x дает наклонную линию, а y=4y=4 дает горизонтальную линию.
Пример 4.18
График y=-3xy=-3x и y=-3y=-3 в одной и той же прямоугольной системе координат.
Решение
Обратите внимание, что в первом уравнении есть переменная xx, а во втором нет. См. Таблицу 4.23. Два графика показаны на рис. 4.17.
| y=−3xy=−3x | у=-3у=-3 | |||||
| хх | г.г. | (х, у) (х, у) | хх | г | (х, у) (х, у) | |
| 0 | 0 | (0,0)(0,0) | 0 | −3−3 | (0,−3)(0,−3) | |
| 1 | −3−3 | (1,−3)(1,−3) | 1 | −3−3 | (1,−3)(1,−3) | |
| 2 | −6−6 | (2,−6)(2,−6) | 2 | −3−3 | (2,−3)(2,−3) | |
Таблица 4.23
Рисунок 4.17
Попробуйте 4.35
График y=-4xy=-4x и y=-4y=-4 в одной и той же прямоугольной системе координат.
Попробуйте 4.36
График y=3y=3 и y=3xy=3x в одной и той же прямоугольной системе координат.
Раздел 4.2 Упражнения
Практика ведет к совершенству
Распознавание взаимосвязи между решениями уравнения и его графиком
В следующих упражнениях для каждой заказанной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения? ⓑ Точка на линии?
55.у=х+2у=х+2
- ⓐ (0,2)(0,2)
- ⓑ (1,2)(1,2)
- ⓒ (−1,1)(−1,1)
- ⓓ (−3,−1 )(−3,−1)
у=х-4у=х-4
- ⓐ (0,−4)(0,−4)
- ⓑ (3,−1)(3,−1)
- ⓒ (2,2)(2,2)
- ⓓ (1,− 5)(1,−5)
у=12х-3у=12х-3
- ⓐ (0,−3)(0,−3)
- ⓑ (2,−2)(2,−2)
- ⓒ (−2,−4)(−2,−4)
- ⓓ (4,1)(4,1)
у=13х+2у=13х+2
- ⓐ (0,2)(0,2)
- ⓑ (3,3)(3,3)
- ⓒ (−3,2)(−3,2)
- ⓓ (−6,0) (−6,0)
График линейного уравнения по точкам
В следующих упражнениях постройте график по точкам.
Вертикальные и горизонтальные линии графика
В следующих упражнениях постройте график каждого уравнения.
В следующих упражнениях постройте график каждой пары уравнений в одной и той же прямоугольной системе координат.
117.y=-12xy=-12x и y=-12y=-12
118.y=-13xy=-13x и y=-13y=-13
Смешанная практика
В следующих упражнениях постройте график каждого уравнения.
Математика на каждый день
135.Стоимость автодома. Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обошлась им в 594 доллара плюс 0,32 доллара за милю, поэтому линейное уравнение y=594+0,32xy=594+0,32x дает стоимость yy проезда xx миль. Рассчитайте стоимость аренды за проезд в 400, 800 и 1200 миль, а затем нарисуйте линию.
136.Еженедельный заработок. В художественной галерее, где он работает, Сальвадор получает 200 долларов в неделю плюс 15% от его продаж, поэтому уравнение y=200+0.15xy=200+0,15x дает сумму yy, которую он зарабатывает за продажу xx долларов произведений искусства. Подсчитайте сумму, которую Сальвадор зарабатывает на продаже 900, 1600 и 2000 долларов, а затем нарисуйте линию.
Письменные упражнения
137.Объясните, как вы выберете три значения x -, чтобы составить таблицу для построения графика линии y=15x−2y=15x−2.
138.В чем разница между уравнениями вертикальной и горизонтальной прямой?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Изучив этот контрольный список, что вы сделаете, чтобы стать уверенным в достижении всех целей?
График линейного уравнения с использованием таблицы значений
Как построить график линейного уравнения
Линейное уравнение — это уравнение с двумя переменными, которые при графическом отображении дают нам прямую линию. Вы, наверное, знаете, как читать график линейного уравнения, но как нам построить график линейного уравнения на координатной плоскости? Оказывается, это на самом деле не так уж и сложно! Первый шаг — научиться составлять таблицу значений.
Что такое таблица значений
Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений. Таблица значений, как следует из ее названия, представляет собой графический способ определения значений, которые будут использоваться для построения графика. Это место, где вы можете записать ответы, которые вы получите, когда найдете значение x и y. Вам нужно будет использовать как минимум 2 набора точек, чтобы построить линейное уравнение, но обычно вы делаете больше в таблице значений.
Таблица значений имеет два столбца.В одном столбце перечислены значения x, а в другом — соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.
Построение графиков линейных уравнений с использованием таблицы значений
Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите построить в виде графика, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с вашей таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите y на оси y.Давайте представим, что вы получили -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце со значениями y.
Выберите другое значение x, с которым вы хотите работать, и снова найдите y. Повторите столько раз, сколько хотите, чтобы разработать наборы значений для помещения в вашу таблицу. Когда вы получите сумму, которой вы довольны или которую задает ваш вопрос, вы можете взять эти значения x и y и отобразить их в виде координат на графике, чтобы отобразить точки в линейном уравнении!
Примеры проблем
Вопрос 1:
График следующей функции с использованием таблицы значений
у = 3х – 1
Решение:
Сначала создайте таблицу значений уравнения.Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одинаковым независимо от того, какие значения вы используете.
Таблица значений хДля х = -2
у = 3(-2) – 1
г = -6 – 1
г = -7
Для х = -1
у = 3(-1) – 1
г = -3 – 1
г = -4
Для х = 0
г = 3(0) – 1
г = 0 – 1
г = -1
Для х = 1
у = 3(1) – 1
г = 3 – 1
г = 2
Для х = 2
у = 3(2) – 1
г = 6 – 1
г = 5
Теперь у нас есть полная таблица значений
Заполненная таблица значений x и yТеперь мы можем нанести упорядоченные пары на сетку
Отображение данныхЗатем соедините точки прямой линией, и готово!
Связывание данных по прямойВопрос 2:
Постройте график следующей функции, используя таблицу значений:
2х + 4у = 8
Решение:
Во-первых, мы хотим упростить уравнение
2х + 4у = 8
х + 2у = 4
2у = -х + 4
y = −12\frac{-1}{2}2−1x + 2
Теперь у нас есть уравнение в форме пересечения наклона.
Затем создайте таблицу значений уравнения. Используйте x, чтобы найти y.
Таблица x решить для yДля х = -2
y = −12\frac{-1}{2}2−1(-2) + 2
у = 1 + 2
г = 3
Для х = -1
y = −12\frac{-1}{2}2−1(-1) + 2
у = 0,5 + 2
г = 2,5
Для х = 0
y = −12\frac{-1}{2}2−1(0) + 2
г = 0 + 2
г = 2
Для х = 1
y = −12\frac{-1}{2}2−1(1) + 2
г = -0.5 + 2
г = 1,5
Для х = 2
y = −12\frac{-1}{2}2−1(2) + 2
г = -1 + 2
г = 1
Теперь у нас есть полная таблица значений
Таблица заполненных данныхМы можем нанести упорядоченные пары на сетку.
Координаты нанесены с использованием таблицы данныхЗатем соедините точки прямой линией, и готово!
Связать данные прямой линиейХотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот онлайн-калькулятор для справки.
Далее узнайте больше о таблице значений, о том, как строить графики линейных неравенств с двумя переменными и как строить графики систем линейных неравенств.

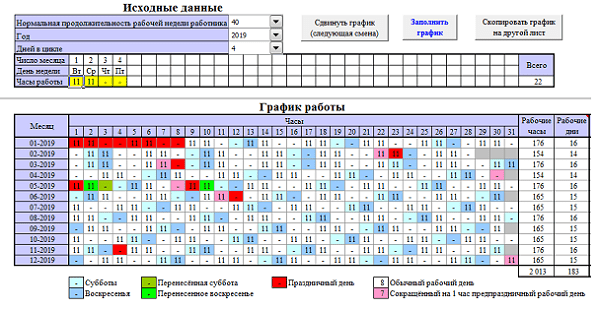 вторник.- работаешь , среда четверг -выходной , пятница ,суббота и воскресенье работаешь . Ну помоему это нереально так работать — каждая пят.субб.воскр работа . Мне кажется это всё таки как плавующие т.е сначала два рабочих , два выходных , три рабочих , дальше два выходных , два рабочих , три выходных . А вы как думаете ? Кто сталкивался с таким графиком ?
вторник.- работаешь , среда четверг -выходной , пятница ,суббота и воскресенье работаешь . Ну помоему это нереально так работать — каждая пят.субб.воскр работа . Мне кажется это всё таки как плавующие т.е сначала два рабочих , два выходных , три рабочих , дальше два выходных , два рабочих , три выходных . А вы как думаете ? Кто сталкивался с таким графиком ? Первая неделя пять дней работаешь, вторую – только два, просто прелесть!
Первая неделя пять дней работаешь, вторую – только два, просто прелесть! Думаю продавцом в магазине тяжеловато , три дня на ногах с утра до вечара .
Думаю продавцом в магазине тяжеловато , три дня на ногах с утра до вечара .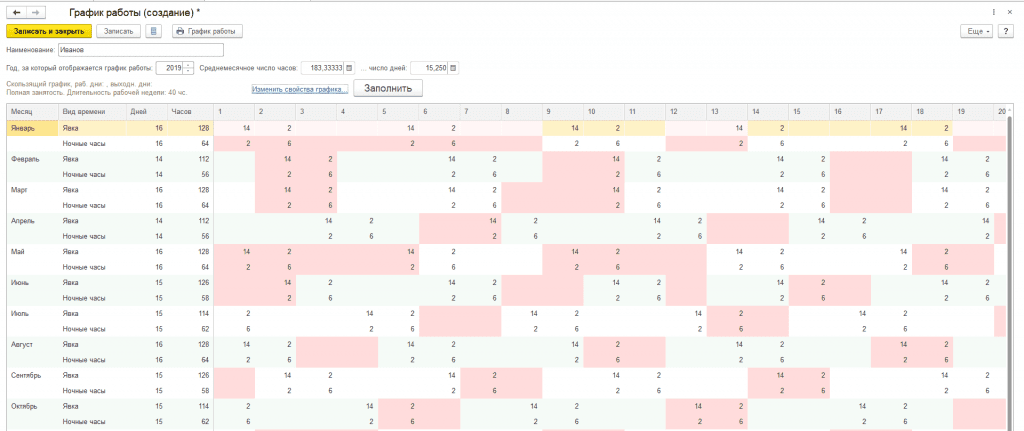 1: Примеры для дальнейшего
1: Примеры для дальнейшего 4: Найти y по x и уравнению прямой
4: Найти y по x и уравнению прямой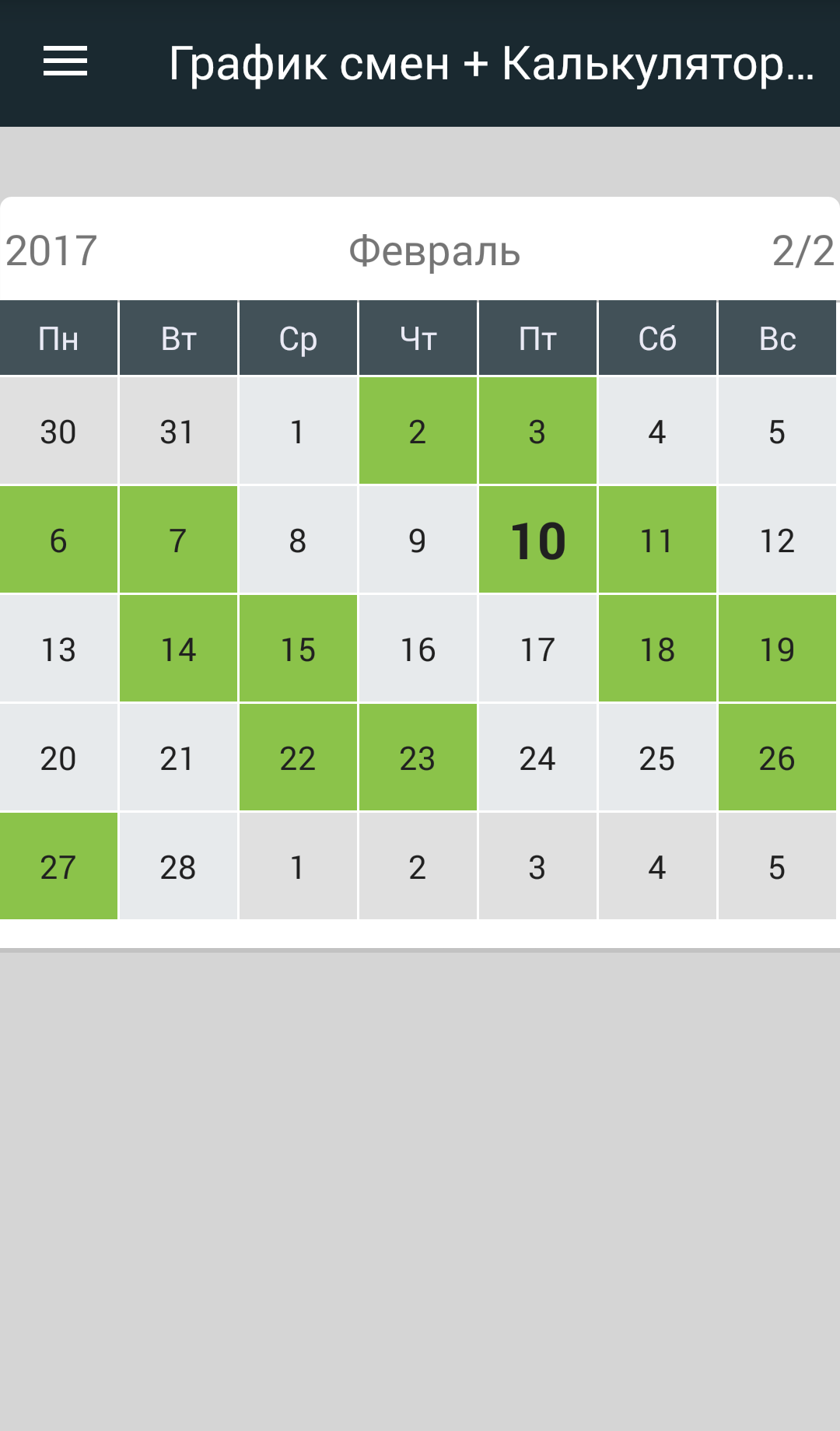 Наклон линии – это подъем над разбегом. Если наклон задан целым или десятичным значением, мы всегда можем поместить его над числом 1. В этом случае линия поднимается на наклон, когда она проходит 1. «Проходит 1» означает, что значение x увеличивается на 1 единицу. Следовательно, наклон показывает, насколько изменяется y при изменении x на 1 единицу.
Наклон линии – это подъем над разбегом. Если наклон задан целым или десятичным значением, мы всегда можем поместить его над числом 1. В этом случае линия поднимается на наклон, когда она проходит 1. «Проходит 1» означает, что значение x увеличивается на 1 единицу. Следовательно, наклон показывает, насколько изменяется y при изменении x на 1 единицу. Теперь мы перейдем к вопросам, которые предполагают сравнение двух переменных. Работа с двумя переменными часто встречается в статистических исследованиях, и мы хотели бы иметь возможность отображать результаты графически. Лучше всего это сделать, нанеся точки в плоскости xy.
Теперь мы перейдем к вопросам, которые предполагают сравнение двух переменных. Работа с двумя переменными часто встречается в статистических исследованиях, и мы хотели бы иметь возможность отображать результаты графически. Лучше всего это сделать, нанеся точки в плоскости xy.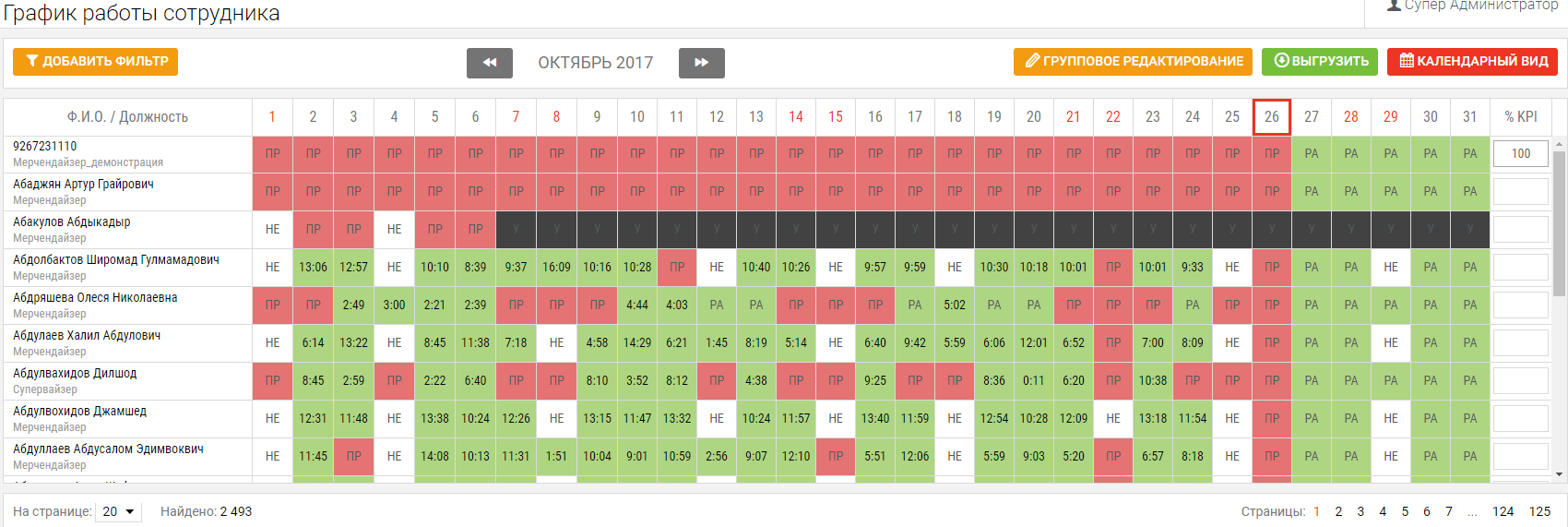
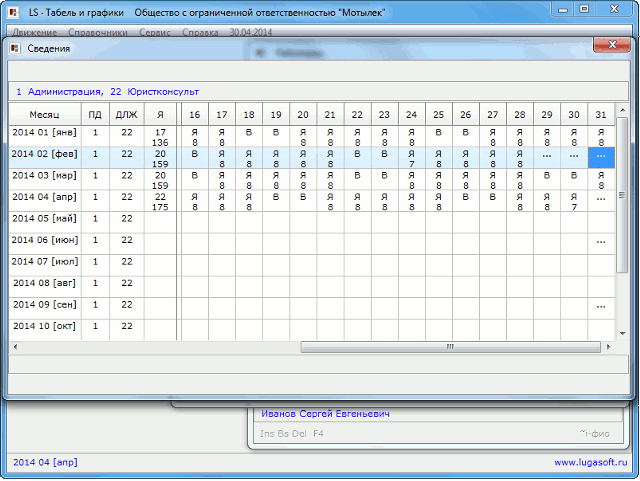

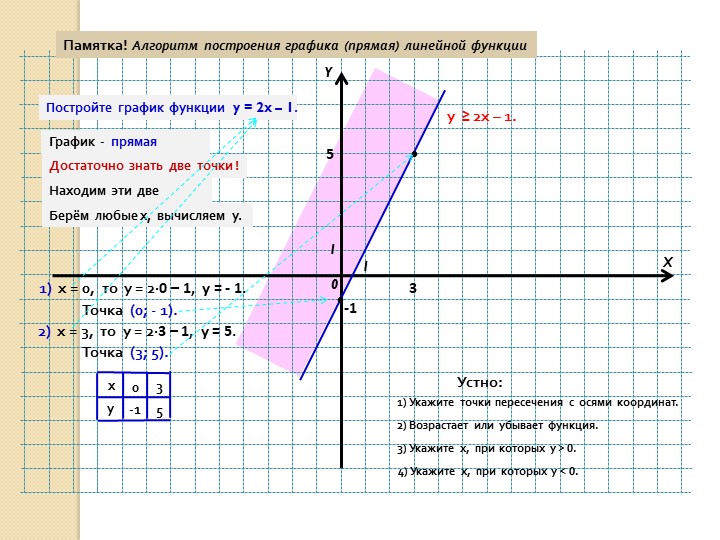 Покажем, что это правда. Возьмите те же две точки (15, 8)
и (10, 7), но на этот раз мы будем вычислять наклон, используя (15,
8) как ( x 1, y 1) и (10, 7) как точка ( x 2, y 2).Затем подставьте их в уравнение для наклона:
Покажем, что это правда. Возьмите те же две точки (15, 8)
и (10, 7), но на этот раз мы будем вычислять наклон, используя (15,
8) как ( x 1, y 1) и (10, 7) как точка ( x 2, y 2).Затем подставьте их в уравнение для наклона: Чем больше наклон, тем круче линия. Держите в
Имейте в виду, вы можете сделать это сравнение только между линиями на графике
если: (1) обе линии проведены на одном наборе осей или (2)
линии нарисованы на разных графиках (т.д., используя разные наборы
осей), где оба графика имеют одинаковый масштаб.
Чем больше наклон, тем круче линия. Держите в
Имейте в виду, вы можете сделать это сравнение только между линиями на графике
если: (1) обе линии проведены на одном наборе осей или (2)
линии нарисованы на разных графиках (т.д., используя разные наборы
осей), где оба графика имеют одинаковый масштаб.