Рассчитываем коэффициент текучести кадров – Компания «АПИ»

       Коэффициент текучести обычно рассчитывается за год, но можно брать и любой другой период. Формула расчета коэффициента такова:

 

            Число уволенных сотрудников/Среднесписочное число сотрудников

 

Сам по себе коэффициент, рассчитанный в числовом или процентном выражении, не несет никакой информации. Важна его динамика — уменьшение или увеличение на протяжении конкретного отрезка времени.

При сборе данных должны быть установлены причины ухода сотрудников. Здесь важно проанализировать, почему они уволились, в каких подразделениях, отделах работали и как долго, насколько ценны эти специалисты для учреждения и что оно теряет с их уходом. Чтобы такие сведения могли быть в полной мере использованы при формировании или уточнении кадровой политики, следует избегать расчетов по принципу «средняя температура по больнице» и сегментировать информацию. Например, целесообразно вести статистику увольнений по кварталам и годам, структурным подразделениям, отдельным должностям, стажу работы в учреждении.

Среди основных причин увольнений по собственному желанию обычно фигурируют несоответствие оплаты трудозатратам, слишком высокая интенсивность труда, нерегламентированный (по факту) рабочий день, сложные отношения с руководством, отсутствие перспектив, удаленность работы от места жительства, выход на пенсию. Из года в год названные причины могут повторяться, но их процентное соотношение, скорее всего, будет разным. На это и должно быть обращено внимание руководства учреждения (в частности, может быть поставлена задача устранить те или иные причины увольнений).

В качестве примера приведем анализ текучести кадров в органах власти одного из субъектов РФ — Республики Башкортостан. Исследование показало, что сменяемость работников, занимающих должности государственной гражданской службы, за 2012 г. составила 46 человек, из них 30 человек работало в республиканском Минэкономразвития, 7 человек — в комитете по тарифам, 9 человек — в комитете по госзаказам. Причины сменяемости кадров различны: 2 человека выдвинуты на повышение, 5 человек вышли на пенсию, 16 человек уволились по собственному желанию, 13 человек перешли на другую работу и 10 человек уволились по иным причинам.

При этом пребывали в должности меньше одного года 12 из 46 человек. Наибольшая сменяемость характерна для категории «специалисты» (33 из 46 человек), из них 30 человек относятся к старшей и 3 — к ведущей группе должностей. Таким образом, коэффициент текучести кадров за отчетный период составил: (46 / 224) чел. x 100% = 21%. В Минэкономразвития данный коэффициент равен 26% ((30 / 116) чел. x 100%), в комитете по тарифам — 18% ((7 / 39) чел. x 100%), в комитете по госзаказам — 16,4% ((9 / 55) чел. x 100%). Вывод: ротация кадров в пределах 20% численного состава в год вполне допустима в органе государственной власти с численностью до 300 сотрудников.

 

Конечно, это далеко не все коэффициенты, которые помогут определить, существует ли в учреждении «кадровый голод». Для анализа можно использовать и другие (например, отражающие специфику деятельности конкретного учреждения).

 

Более подробно с данным материалом Вы можете ознакомиться в СПС КонсультантПлюс

Статья: Кадровый дефицит: решаем проблему силами учреждения (Жулькова Ю. Н.) («Руководитель автономного учреждения», 2015, N 12) {КонсультантПлюс}

Интер РАО — Сотрудники

Один из ключевых принципов корпоративной политики «Интер РАО» заключается в том, что главным активом компании являются ее сотрудники. В этой связи компании Группы уделяют важное значение вопросам охраны труда, обеспечению максимальной защищённости и безопасности своих сотрудников, занятых на производстве.

48 851 чел.	Списочная численность сотрудников Группы
> 71 %	Процент сотрудников, моложе 50 лет
3,8 %	Коэффициент текучести кадров (*в расчете по уволенным сотрудникам)

Интер РАО обладает сбалансированным с точки зрения структуры, опыта и профессиональных компетенций штатом сотрудников, что позволяет эффективно решать операционные и стратегические задачи. Кадровая политика Группы развивается на базе единой системы менеджмента, основу которой составляют корпоративные ценности.

Списочная численность персонала Группы на 31.12.2020 составила 48 851 человек, что на 0,3% больше численности на ту же дату годом ранее. Более 71% персонала Группы моложе 50 лет. Несмотря на традиционное для энергетической отрасли профессиональное смещение гендерного баланса в сторону работников-мужчин, в структуре персонала Компании доля женщин сравнительно велика – 43,3% от списочной численности. С 94,4% всех работников заключены трудовые договоры на неопределённый срок. 95,8% работников оформлены на полную рабочую неделю. Оба показателя сохраняют положительную динамику предыдущих лет.

Эффективная кадровая политика и разнообразные методы подбора персонала, традиционно применяемые в «Интер РАО», позволяют удерживать показатель укомплектованности персонала на высоком уровне в 94,6%. Коэффициент текучести кадров в расчёте по уволенным сотрудникам в 2020 г. по собственному желанию и за нарушение трудовой дисциплины составил 3,8%.

При найме персонала Группа в полной мере и в соответствии с законодательством обеспечивает подход, исключающий любые виды дискриминации. Во внутренних нормативных документах Группы отражены положения о недопущении в компаниях Группы любых форм дискриминации или притеснения по любым основаниям, включая национальность, пол, возраст. Специальные политики в области гендерного таргетирования в отчётном году не применялись.

Основные направления и результаты реализации кадровой политики

В 2020 г. приоритетными мероприятиями и направлениями деятельности кадровой политики являлись:

• развитие направления «Корпоративная социальная ответственность» и молодёжной политики;
• внедрение Корпоративного университета;
• пересмотр системы грейдирования;
• развитие направления «Операционная эффективность»;
• автоматизация HR-процессов на базе Mirapolis HCM;
• качественное изменение подхода к формированию кадрового резерва.

Что такое коэффициент текучести кадров? –

Как рассчитать коэффициент текучести кадров?

Чтобы рассчитать текучесть, используйте стандартную формулу Ктек = Кув × 100 (%) : S.

Где Ктек — коэффициент текучести персонала; Кув — количество уволенных сотрудников за рассматриваемый период; S — среднесписочная численность персонала за рассматриваемый период.22 авг.

2019 г.

Как рассчитать текучесть кадров за квартал?

Расчет текучести персонала

• Шаг 1: Рассчитайте численность персонала
• Шаг 2: Рассчитайте среднюю численность персонала
• Шаг 3: Рассчитайте количество уволившихся
• Шаг 4: Разделите количество уволившихся на среднюю численность персонала
• Шаг 5: Рассчитайте текучесть кадров
• Шаг 6: Показатель текучести персонала за год

18 сент. 2017 г.

Какие показатели характеризуют движение рабочей силы?

Относительные показатели характеризуют степень интенсивности движения рабочей силы: 1) коэффициент оборотов по приему; Показатель текучести рабочей силы – это совокупность работников, уволенных по собственному желанию, как не прошедших испытательного срока, за нарушения трудовой дисциплины.

Как рассчитать коэффициент общего оборота кадров?

Рассмотрим показатели, характеризующие движение рабочей силы: Коэффициент оборота по приему это число принятых на работу деленное на среднесписочную численность рабочих за данный период. Коэффициент оборота по увольнению это число уволенных с работы, деленное на среднесписочную численность рабочих за данный период.

Как рассчитывается текучесть кадров на предприятии?

КОЭФФИЦИЕНТ ТЕКУЧЕСТИ КАДРОВ — отношение числа уволенных работников предприятия, выбывших за данный период по причинам текучести (по собственному желанию, за прогулы, за нарушение техники безопасности, самовольный уход и т.п. причинам, не вызванным производственной или общегосударственной потребностью) к

Как рассчитать среднесписочную численность работников?

Чтобы рассчитать ССЧ за конкретный месяц, сложите списочную численность работников за каждый календарный день и разделите на количество календарных дней в месяце. 24 дек. 2018 г.

Как определить обеспеченность предприятия трудовыми ресурсами?

Обеспеченность предприятия трудовыми ресурсами определяется сравнением фактического количества работников по категориям и профессиям с плановой потребностью. Особое внимание уделяется анализу обеспеченности предприятия кадрами наиболее важных профессий.

Что такое сменяемость кадров?

Сменяемость кадров Определяется как отношение всех уволенных в течение года работников к общему их составу. Аналогично рассчитывают показатели полного периода сменяемости кадров по отдельным категориям работников и профессиональным группам.

Что такое оборот кадров?

Интенсивность оборота кадров характеризуется коэффициентом общего оборота по приему, который представляет собой отношение числа принятых за отчетный период к среднесписочной численности работников за тот же период, и по увольнению, который представляет собой отношение уволенных за отчетный период к среднесписочнои

Что такое движение кадров?

Движение кадров представляет собой изменение места и сферы приложения труда, рода деятельности и производственных функций работников. На предприятии существует профессиональное движение (овладение смежными профессиями, второй специальностью), и квалификационное движение (повышение разряда).

Коэффициент текучести материала – Справочник химика 21

    Допускаемые напряжения для сечения толщиной 5 1 [О]) предел текучести материала фланца при нормальной температуре т — коэффициент, учитывающий свойства среды (для взрывоопасных и токсичных сред 1 -= 0,85 4-0,90).  [c.101]

    Для оценки поведения сыпучего материала под действием внешней нагрузки используют несколько характеристик угол естественного откоса а, начальное сопротивление сдвигу То, угол внутреннего трения ср, коэффициент внутреннего трения /, коэффициент внешнего трения коэффициент размалываемости Кр, коэффициент бокового давления I, коэффициент текучести К,- [c. 152]

    Напряжение является единственным ненулевым главным напряжением, поскольку предполагается, что свод самоподдерживается. И ст , и — линейные функции ширины загрузочного устройства, а их отношение для данного устройства постоянно. Коэффициент подвижности зависит от геометрии загрузочного устройства и свойств материала его значения рассчитаны для ряда загрузочных устройств и материалов с разными свойствами. Предел текучести уплотненного материала устойчивого свода определяется пределом текучести материала в ненагруженном состоянии который в свою очередь является функцией напряжения сжатия Поэтому условие, при котором свод не образуется, состоит в следующем  [c.235]

    Способность сыпучего материала вытекать из отверстий в стенках машин и аппаратов оценивают коэффициентом текучести Кт, который определяют по времени истечения 1 порошка из калиброванной воронки [c.154]

    Из формулы (5. 3) видно, что для определения изгибающих моментов в каждом сечении правящейся полосы необходимо знать размеры последней, предел текучести материала и коэффициент упругой зоны. [c.88]

    Скорость прессования, под которой понимают скорость движения прессующего пуансона, существенно влияет на величину давления прессования. Физическая природа явлений, происходящих при прессовании сыпучего материала с высокими скоростями, очень сложна. При этом могут изменяться физические свойства частиц материалов пределы прочности и текучести материала, коэффициенты внешнего и внутреннего трения частиц, характер деформаций. Помимо этого, на процесс прессования оказывает влияние воздух, запрессованный между частицами порошка таблетки. [c.207]

    Отметим некоторые особенности растяжения такого образца. Для сталей различие в коэффициентах упругости невелико, поэтому в дальнейшем считаем их равными. Тогда при растяжении в пределах упругости образец находится в состоянии равномерного одноосного растяжения. При достижении предела текучести материала диска последний сразу и полностью переходит в пластическое состояние. С развитием пластических деформаций напряженное состояние диска все более отклоняется от равномерного растяжения и приобретает сложный пространственный характер, так как деформированию диска препятствуют жесткие части образца, остающиеся упрут ими. При этом на плоскостях контакта слоя с жесткими частями развиваются касательные напряжения. Наибольшее значение последних определя ется пределом текучести Тз. [c.63]

    Е, Ех и V VI – значения модуля Юнга и коэффициента Пуассона материала образца и индентора соответственно. Значение динамического предела текучести Ро зависит от скорости соударения и при малых скоростях удара приближается к значению статической твердости, а при больших скоростях превышает его в 2-3 раза. [c.207]

    Для переходных режимов работы предельное напряжение принимают равным пределу текучести материала / ро,2, деленному на коэффициент  [c. 324]

    За пределами упругости, при отсутствии упрочнения, интенсивность напряжений во всех точках пластической области равна пределу текучести материала. Поэтому, если определить теоретический коэффициент концентрации напряжений как отношение эквивалентных напряжений, то величина его для принятого отношения р = 0,8 0 равна обратному значению этого отношения, т. е. 1,25. Если же теоретический коэффициент концентрации напряжений определять как отношение наибольших главных напряжений, то его величина будет в соответствии с расчетом равна 1,43. Таким образом, независимо от способа определения эффективного коэффициента концентрации величина его уменьшается с развитием пластических деформаций [1]. [c.214]

    Было замечено, что текучесть материала резко возрастает с увеличением амплитуды и, следовательно, ускорения колебаний. Одновременно коэффициент теплоотдачи к вибрирующему слою увеличивается от АБ,5 вт м- – град- (39 ккал – м град-i) ggg вибрации до 194 вТ М- град (166 ккал м- град- ) при вибрации, т. е. возрастает более чем в 4 раза. Опыты показали, что основным параметром, влияющим нг [c.152]

    Здесь Р — давление в камере = а 1п, где — предел текучести материала экрана п — коэффициент запаса прочности. [c.83]

    Чем меньше коэффициент вязкости материала, тем больше его текучесть. Если известны коэффициенты вязкости при наименьшей скорости сдвига (0,015 i) и при повышенной скорости сдвига (например, при 15 с 1), то отношение этих коэффициентов характеризует степень пластикации материала за счет сдвиговых деформаций. [c.21]

    В формулах (134) и (135) — нормативное сопротивление, равное наименьшему значению временного сопротивления разрыву материала труб и, сварных соединений, кгс/см Да — нормативное сопротивление, равное наименьшему значению предела текучести при растяжении, сжатии и изгибе материала труб и сварных соединений, кгс/см кг и к — коэффициенты однородности материала труб 7Wi и /П2 — коэффициенты условий работы соответственно материала при разрыве труб и трубопровода  [c. 186]

    Давление при охлаждении в любой момент должно превышать предел текучести материала. Это предотвращает образование усадочных раковин и пустот, обусловливаемых большим значением коэффициента термического расширения полиэтилена (например, для полиэтиленов-1 и П давление в начале охлаждения при температуре около 120° должно быть 5 кг см , к концу охлаждения при температуре в середине блока 60—70° примерно 60 кг/см ). [c.196]

    При определении технической нормы расхода учитывают минимальную навеску, предел точности ее, а также поправочные коэффициенты на текучесть материала и на точность дозирования. [c.326]

    Прибор для определения коэффициента текучести К имеет (рис. 8) конусную стеклянную воронку 1, закрепленную в стойке 2, опирающейся на подставку 5. Угол конусности воронки равен 60°. Диаметр нижнего отверстия в зависимости от крупности частиц сыпучего материала принимают равным 1—7 мм. Трубка воронки срезается на расстоянии 3 мм от нижнего основания конуса и закрывается заслонкой 3.  [c.23]

    Применение металлизационных грунтовок. Коэффициенты теплового линейного расширения высокополимеров значительно больше, чем у металлов. Напряжения, возникающие в покрытии при охлаждении его после нанесения, вследствие различия в коэффициентах теплового линейного расширения металла и полимера, благоприятствуют адгезии, когда они нанесены на выпуклые поверхности и стремятся оторвать покрытие, нанесенное на вогнутые поверхности. Если покрытие на вогнутых поверхностях обладает упругими свойствами, например эбонитовое, то напряжения, возникающие в нем, компенсируются упругими деформациями. Напряжения в покрытиях могут компенсироваться также текучестью материала при пластических деформациях. [c.295]

    Недостатком этого метода оценки текучести сыпучих материалов является то, что измерения производятся при условиях, значительно отличающихся от условий дозирования материалов в таблеточных машинах. Поэтому наблюдаются случаи, когда коэффициент текучести равен нулю (материал зависает в воронке), однако материал успешно дозируется на таблеточных машинах. По этой причине при определении текучести порошков химико-фармацевтических препаратов воронку устанавливают на штативе с электровибратором ЭЛ-1 (частота колебаний 100 Гц). [c.19]

    Различие в прочностных свойствах хрупких и пластичных материалов характеризуется коэффициентом К, равным отношению предела текучести Оъ при растяжении к пределу текучести материала на сжатие [c.114]

    Коэффициент текучести характеризует способность сыпучего материала вытекать из отверстий. Он определяется по времени / истечения материала из калиброванной воронки. Для металлических порошков значения кг берутся из ГОСТ 20899-98. [c.128]

    Пластификаторами служат высококипяш,ие вязкие жидкости, например сложные эфиры фталевой и себациновой кислот, растворимые в полимере, а также легкоплавкие синтетические воскоподобные вещества, хорошо совмещающиеся с полимером. В присутствии пластифицирующих добавок облегчается скольжение макромолекул размягченного полимера друг относительно друга, т. е. повышается текучесть материала. Пластификатор должен оставаться и в готовых изделиях, благодаря чему повышается их упругость, эластичность и морозостойкость, но снижается теплостойкость и ухудшаются диэлектрические характеристики, увеличивается коэффициент объемного термического расширения и возрастает ползучесть (хладотекучесть) материала под нагрузкой. Жидкие пластификторы постепенно улетучиваются из изделий, что вызывает их коробление и изменение физико-механических свойств (старение пластифицированных полимеров). Поэтому Б производстве пластических масс стремятся использовать воскоподобные пластификаторы. Количество пластификатора, вводимого в состав термопластичного полимера, можно варьировать в широких пределах в зависимости от требований, которые предъявляются к готовым изделиям. [c.529]

    Другая проблема, возникающая при использовании коэффициента К в расчетах, связана с применением его при асимметричных циклах нагружения, т. е. когда учитывается как в среднем, так и в амплитудном переменном напряжении цикла. Наиболее часто используют /(/ только для определения переменной Аг/ компоненты цикла. Но лучше учитывать при расчете как среднего, так и переменного напряжения цикла. Однако при этом необходимо принимать во внимание снижение среднего напряжения при увеличении максимального напряжения цикла выше предела текучести. Возьмем, например, образец в виде бруса из материала с пределом текучести 28 кгс/мм и с надрезом Kf = 3. Образец подвергается циклической нагрузке при растяжении с номинальными напряжениями в интервале О— 14 кгс/мм . По общепринятой терминологии среднее напряжение составляет 7 кгс/мм , а расчетная амплитуда напряжения равна 21 кгс/мм . По рекомендованному методу базовое (исходное) среднее напряжение составит 21 кгс/мм , и его откорректированная в соответствии с выражением (2.3) величина будет равна 7 кгс/мм . Таким образом, текучесть в течение первых нескольких циклов, по всей вероятности, свидетельствует в пользу общепринятой методики расчета компонента среднего напряжения при неучете коэффициента Kf. Например, если предел текучести материала составляет 35 кгс/мм , то откорректированное среднее напряжение будет равно 14 кгс/мм , и в этом случае общепринятая методика дает надежный результат. Предлагаемый выше метод был описан Хейгом [19] в 1929 г. и использовался примерно до 1960 г. он полезен в том случае, когда действительное среднее напряжение входит в оценку усталостной прочности, однако его не следует применять, если используемая для оценки долговечности кривая усталости откорректирована с учетом максимально возможного влияния среднего напряжения (см. рис. 2.11). [c.72]

    Расчет на прочность производится в следующем порядке. Расчетное сопротивление материала труб и их соединений / 1 определяется по формуле Я = Я к тхГП2. Расчетное сопротивление материала труб и их соединений / 2 определяется по формуле 2 = =Я2 к2П12тз, где нормативное сопротивление, равное наименьшему значению временного сопротивления разрыву материала труб и сварных соединений, принимаемое по стандартам или техническим условиям на соответствующие виды труб, МПа — нормативное сопротивление, равное наименьшему значению предела текучести при растяжении, сжатии и изгибе материала труб и сварных соединений, принимаемое по стандартам или техническим условиям на соответствующие виды труб, МПа Ь — коэффициенты однородности материала труб, принимаемые по табл. 11.13 т.1 — коэффициент условий работы материала при раз- [c.535]

    Максимальные напряжения не должны превышать предела текучести материала кольца при растяжении (сжатии), так как в случае появления остаточных деформаций уменьшится давление между листами сердечника. В нашем случае материал плиты — немагнитная сталь с пределом текучести при растяжении = 16 кПмм Коэффициент запаса равен 16/12,4 = 1,29, что достаточно. [c.311]

    Для оценки возможности повреждения аппарата или трубопровода необходимо сравнить найденное максимальное значение действительного температурного напряжения с пределом текучести материала стенки трубы или аппарата Сттек- Условие опасности с учетом коэффициента запаса можно представить в виде [c.42]

    При расчетах по допускаемым напряжениям коэффициент запаса вычисляют как отношение предела текучести материала к максимальному напряжению. При обычно наблюдаемом неоднородном нагружении материала полых резино-текстильных изделий возникновение в какой-либо одной наиболее напряженной точке (или области) пластических деформаций еще не означает выхода нз строя всей конструкции. Поэтому, при расчетах по предельному состоянию, определяют величину предельных нагрузок, при которых исчерпывается несущая способность (прочность или устойчивость) всего изделия, или же определяют деформацию (по прогибам или по складкообразованию), ведущую к выходу из строя конструкции или ее элемента, а коэффициент запаса вычисляют как отношение предельной нагрузки к действительной. Применение этого метода позволяет создавать более э1 номичные конструкции, поскольку здесь вскрываются дополнительные прочностные и деформационные ресурсы конструкций, не учитываемые в методе расчета по допускаемым напряжениям. [c.113]

    При расчете по модифицированным формулам стандарта ANSI/ASME В 31G трубопроводов, контактирующих с наводороживающими средами и содержащих внутренние и поверхностные нетрещиноподобные дефекты, за напряжение текучести принимают нормативный предел текучести материала (S = Oj. ). Коэффициент запаса прочности определяют по формуле [c.178]

---

Калькулятор расхода – Давление и диаметр

Калькулятор расхода – Давление и диаметр | Копели

С помощью этого инструмента можно легко рассчитать средний объемный расход жидкости, изменив каждую из трех переменных: длину, давление и диаметр отверстия. Затем влияние на прогнозируемый расход отображается на трех графиках, где, в свою очередь, две переменные поддерживаются постоянными, а расход отображается в зависимости от диапазона значений третьего.

Помните, что если вам нужна помощь в выборе шланга, подходящего для вашего применения или отрасли, свяжитесь с одним из наших сотрудников по телефону 0116 240 1500 или по электронной почте [email protected].

Находите этот инструмент полезным? Вы можете встроить наш калькулятор скорости потока на свой веб-сайт, скопировав приведенный ниже код.

Как использовать:

Чтобы начать расчет, введите свои цифры в поля ниже. Если значение какой-либо из переменных недоступно, оставьте поле пустым, и программа выберет свое значение.

Результаты

Нажмите на вкладки ниже, чтобы просмотреть результаты.

Объемный расход жидкости в зависимости от длины шланга Количество расхода жидкости в зависимости от давления Объемный расход жидкости в зависимости от диаметра отверстия

Количество Расход жидкости в зависимости от длины шланга
Длина	20. 000	40.000	60.000	80.000	100.000	120.000	140.000	160.000	180.000	200.000
Количество Расход жидкости (литров в минуту)	95,273	68.458	56.202	48.807	43,727	39,961	37.026	34.656	32.689	31.023
Диаметр отверстия (мм)	25	25	25	25	25	25	25	25	25	25
Давление (бар)	7	7	7	7	7	7	7	7	7	7
Диаметр отверстия (дюймы)	0.984	0,984	0,984	0,984	0,984	0,984	0,984	0,984	0,984	0,984
Давление (psi)	102. 900	102.900	102.900	102.900	102.900	102.900	102.900	102.900	102.900	102.900
Длина (футы)	65,667	131.333	197.000	262,667	328.333	394.000	459,667	525.333	591.000	656,667
Количество Расход жидкости (галлонов в минуту)	20.960	15.061	12.364	10,738	9,620	8,791	8.146	7,624	7,192	6,825
Коэффициент С	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105
Скорость V (фут/сек)	10.602	7,618	6,254	5.431	4,866	4,447	4. 120	3,856	3,638	3,452
Диаметр отверстия (футы) D	0.082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021
Эквивалент жидкости напора h (фут)	237,644	237,644	237,644	237,644	237.644	237,644	237,644	237,644	237,644	237,644

Количество Данные о расходе жидкости и давлении
Давление	1.400	2.800	4.200	5.600	7.000	8.400	9.800	11.200	12.600	14.000
Количество расхода жидкости (л/мин)	19.555	27.655	33. 871	39.110	43,727	47.900	51,738	55.310	58.666	61.839
Диаметр отверстия (мм)	25	25	25	25	25	25	25	25	25	25
Длина	100	100	100	100	100	100	100	100	100	100
Диаметр отверстия (дюймы)	0.984	0,984	0,984	0,984	0,984	0,984	0,984	0,984	0,984	0,984
Давление (psi)	20.580	41.160	61.740	82.320	102.900	123.480	144.060	164.640	185.220	205.800
Длина (футы)	328.333	328. 333	328.333	328.333	328.333	328.333	328.333	328.333	328.333	328.333
Количество расхода жидкости (гал/мин)	4.302	6.084	7,452	8.604	9,620	10,538	11.382	12.168	12.906	13.605
Коэффициент С	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105	20.105
Скорость V (фут/сек)	2,176	3,077	3,769	4,352	4,866	5.330	5,757	6.155	6,528	6,881
Диаметр отверстия (футы) D	0.082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021	0,082021
Эквивалент жидкости напора h (фут)	47,529	95. 058	142,587	190.115	237.644	285,173	332.702	380.231	427.760	475.289

Количество Расход жидкости в зависимости от диаметра отверстия
Диаметр отверстия	5.000	10.000	15.000	20.000	25.000	30.000	35.000	40.000	45.000	50.000
Количество расхода жидкости (л/мин)	0,091	2,204	8,792	21,989	43,727	75.790	119,849	177,478	250,177	339.374
Давление (бар)	7	7	7	7	7	7	7	7	7	7
Длина	100	100	100	100	100	100	100	100	100	100
Диаметр отверстия (дюймы)	0. 197	0,394	0,591	0,787	0,984	1,181	1,378	1,575	1,772	1,969
Давление (psi)	102.900	102.900	102.900	102.900	102.900	102.900	102.900	102.900	102.900	102.900
Длина (футы)	328.333	328.333	328.333	328.333	328.333	328.333	328.333	328.333	328.333	328.333
Количество расхода жидкости (гал/мин)	0.020	0,485	1,934	4,838	9,620	16.674	26.367	39.045	55.039	74,662
Коэффициент С	2,314	9,976	14.458	17.638	20.105	22.120	23.824	25. 300	26.602	27.767
Скорость V (фут/сек)	0,252	1,533	2,718	3,823	4,866	5,857	6.804	7,715	8,592	9.441
Диаметр отверстия (футы) D	0.016	0,033	0,049	0,066	0,082	0,098	0,115	0,131	0,148	0,164
Эквивалент жидкости напора h (фут)	237,644	237,644	237,644	237,644	237,644	237.644	237,644	237,644	237,644	237,644

Расход жидкости в трубах

Количество жидкости, которое будет сбрасываться через шланг, зависит от давления на конце подачи, длины шланга и диаметра отверстия. Характер поверхности отверстия, количество и форма изгибов на участке шланга также влияют на скорость потока.

Давление иногда указывается как «напор водяного столба». Если напор указан в метрах водяного столба, каждый 1 метр напора (3,28 фута) создает давление 0,1 бар (1,47 фунта на кв. дюйм).

Все формулы для нахождения количества жидкости, которая потечет через шланг в данный момент времени, являются приблизительными. Приведенные выше графики построены на основе расчетов, предполагающих, что шланг находится в хорошем состоянии и проложен прямолинейно. При этом они будут иметь точность в пределах 10% от фактически полученных результатов.

Если набор условий, введенных в модель, приводит к отрицательным результатам, то, очевидно, необходимо соответствующим образом скорректировать переменные, пока не будет получен реалистичный результат.

Необходимо рассчитать падение давления жидкости, движущейся по трубе или трубопроводу? Воспользуйтесь нашим калькулятором падения давления.

Вставьте этот инструмент на свой веб-сайт

Скопируйте приведенный ниже код, чтобы встроить калькулятор скорости потока на свой веб-сайт.

Не пропустите последние новости

Подпишитесь на нашу эксклюзивную рассылку по электронной почте, чтобы получать последние новости и предложения от Copely.

Copely Developments Ltd будет использовать информацию, предоставленную вами в этой форме, чтобы время от времени связываться с вами
по поводу интересных историй, новых продуктов и предстоящих событий. Вы можете отписаться в любое время.

© 2022 Copely Developments Ltd – Thurmaston Lane, Leicester, LE4 9HU. – Входит в группу компаний COBA.

12.1 Расход и его связь со скоростью

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Рассчитать расход
• Определение единиц объема
• Описать несжимаемые жидкости
• Объясните следствия уравнения неразрывности

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

• 5. F.1.1 Учащийся может производить расчеты величин, связанных с потоком жидкости, используя принципы сохранения массы, такие как уравнение неразрывности. (Ст.6.4, 7.2)

Скорость потока Размер QQ 10{Q} {} определяется как объем жидкости, проходящей через некоторое место через область в течение определенного периода времени, как показано на рис. 12.2. В символах это можно записать как

. 12.1 Q=Vt,Q=Vt, размер 12{Q= {{V} над {t} } } {}

, где VV размер 12{V} {} — объем, а tt размер 12{t} {} — прошедшее время.

Единицей СИ для расхода является м3/см3/с размер 12{м rSup { размер 8{3} } “/с”} {}, но ряд других единиц для QQ размер 12{Q} {} находятся в общем употреблении. Например, сердце покоящегося взрослого человека перекачивает кровь со скоростью 5 литров в минуту (л/мин). Обратите внимание, что литр (л) равен 1/1000 кубического метра или 1000 кубических сантиметров (10-3м3(10-3м3 размер 12{“10” rSup { размер 8{ – 3} } `м rSup { размер 8{3} } м rSup { размер 8{3} } } } {} <sup>или 103cm3103cm3 размер 12 {“10″ rSup { размер 8{3} } `”см” rSup { размер 8{3} } } {}).В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.</sup>

Рис. 12.2 Расход — это объем жидкости в единицу времени, протекающий через точку через площадь A.A. размер 12{A} {} Здесь заштрихованный цилиндр жидкости течет мимо точки PP размера 12{P} {} в однородной трубе за время t.t. size 12{t} {} Объем цилиндра Ad,Ad, size 12{ ital “Ad”} {} и средняя скорость v¯=d/t,v¯=d/t, size 12{ { overline {v}} =d/t} {}, так что скорость потока Q=Ad/t=Av¯Q=Ad/t=Av¯ size 12{Q= ital “Ad”/t=A {overline {v}} } {}.

Пример 12.1 Расчет объема по скорости потока: сердце перекачивает много крови за всю жизнь

Сколько кубометров крови перекачивает сердце за 75 лет жизни при средней скорости потока 5 л/мин?

Стратегия

Время и расход QQ размера 12{Q} {} заданы, поэтому объем VV размера 12{V} {} можно рассчитать из определения расхода.

Раствор

Решение Q=V/tQ=V/t size 12{Q=V/t} {} для объема дает

12.2 V=Qt.V=Qt. размер 12 {V = итал. “Qt”} {}

Замена известных значений дает

12,3 В=5L1 мин(75 лет)1м3103L5,26×105мин=2,0×105 м3.V=5L1 мин(75лет)1м3103L5,26×105мин=2,0×105 м3.alignl { stack { размер 12{V= влево ( { {5 “.” “00” “L”} более {“1 мин”} } вправо ) \( “75”” y” \) влево ( { {1″ m” rSup { размер 8{3} } } более {“10” rSup { размер 8{3} } “L”} } справа ) слева (5 “.” “26” умножить на “10” rSup { размер 8{5} } { { “min”} над {y} } справа )} {} # ” “=2 “.” 0 раз “10” rSup { размер 8{5} } ” m” rSup { размер 8{3} } {} } } {}

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом бассейне с шестью дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки.Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом QQ размера 12{Q} {} и скоростью v¯v¯ размера 12{ {над чертой {v}} } {} составляет

12,4 Q=Av¯,Q=Av¯, размер 12{ Q=A {над чертой {v}} } {}

, где AA размер 12{A} {}  – площадь поперечного сечения, а v¯v¯ размер 12{ {над чертой {v}} } {} – среднее значение скорость.Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости, далее называемой скоростью, так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. На рис. 12.2 показано, как получается это соотношение. Заштрихованный цилиндр имеет объем

12,5 V=Ad,V=Ad, размер 12{V= ital “Ad”} {}

, которая проходит мимо точки PP размером 12{P} {} за время t. т. size 12{t} {} Разделив обе стороны этого соотношения на tt size 12{t} {} , мы получим

12,6 Vt=Adt.Vt=Adt. размер 12{ { {V} над {t} } = { { ital “Объявление”} над {t} } } {}

Заметим, что Q=V/tQ=V/t размер 12{Q=V/t} {} и средняя скорость v¯=d/tv¯=d/t size 12{ {overline {v}} =d/t} {}. Таким образом, уравнение принимает вид Q=Av¯Q=Av¯ size 12{Q=A {overline {v}} } {}.

На рис. 12.3 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока.В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2

12.7 Q1=Q2A1v¯1=A2v¯2}.Q1=Q2A1v¯1=A2v¯2}. размер 12 { ничего не осталось матрица { Q rSub { размер 8{1} } =Q rSub { размер 8{2} } {} ## A rSub { размер 8{1} } {перечеркнутый {v rSub { размер 8{1} } }} =A rSub { размер 8{2} } {надчеркнутый {v rSub {размер 8{2} } }} } правая фигурная скобка “. ” } {}

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: Это назначение сопла. И наоборот, когда река впадает в один конец водоема, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается при поперечном сечении площадь уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок 12.3. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей.Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Выполнение соединений: несжимаемая жидкость

Уравнение непрерывности говорит нам, что скорость потока должна быть одинаковой во всей несжимаемой жидкости. Скорость потока Q выражена в единицах объема в единицу времени (м ³ /с). Другой способ думать об этом – это принцип сохранения, согласно которому объем жидкости, протекающей через любую точку за заданный промежуток времени, должен сохраняться во всей жидкости.

Для несжимаемых жидкостей мы также можем сказать, что масса, протекающая мимо любой точки за заданный промежуток времени, также должна сохраняться. Это потому, что масса данного объема жидкости равна плотности жидкости, умноженной на объем

.

Когда мы говорим, что жидкость несжимаема, мы имеем в виду, что плотность жидкости не меняется. В каждом кубическом метре жидкости содержится одинаковое количество частиц. Нет места для добавления новых частиц, и жидкость не может расширяться, чтобы частицы рассыпались.Поскольку плотность постоянна, мы можем выразить принцип сохранения следующим образом для любых двух областей течения жидкости, начиная с уравнения неразрывности:

12.10 ρV1t1=ρV2t2ρV1t1=ρV2t2

В более общем смысле мы говорим, что массовый расход (ΔmΔt)(ΔmΔt) сохраняется.

Пример 12.2 Расчет скорости жидкости: скорость увеличивается при сужении трубы

Насадка радиусом 0,250 см крепится к садовому шлангу радиусом 0,900 см. Расход через шланг и сопло равен 0.500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для сопла.

Раствор для (а)

Сначала мы решаем Q=Av¯Q=Av¯ size 12{Q=A {overline {v}} } {} для v1v1 size 12{v rSub { size 8{1} } } {} и заметим, что крест -площадь сечения A=πr2,A=πr2, размер 12{A=πr rSup { размер 8{2} } } {} дает

12. 12 v¯1=QA1=Qπr12.v¯1=QA1=Qπr12. size 12{ {overline {v rSub { size 8{1} } }} = { {Q} over {A rSub { size 8{1} } } } = { {Q} over {πr rSub { size 8{1} rSup { size 8{2} } } } } } {}

Замена известных значений и соответствующее преобразование единиц дает

12.13 v¯1=(0,500л/с)(10-3м3/л)π(9×10-3м)2=1,96м/св¯1=(0,500л/с)(10-3м3/л)π( 9×10−3м)2=1,96 м/с. size 12{ {overline {v rSub { size 8{1} } }} = { { \( 0 “.” “500”” л/с” \) \( “10” rSup { size 8{- 3} } ” m” rSup { size 8{3} } /L \)} над {π \( 9 “.” “00” умножить на “10” rSup {размер 8{ – 3} } ” m” \) rSup { размер 8{2} } } } =1 “.” “96”” м/с”} {}

Решение для (б)

Мы могли бы повторить этот расчет, чтобы найти скорость в сопле v¯2,v¯2, размер 12{ {overline {v rSub { размер 8{2} } }} } {}, но мы будем использовать уравнение неразрывности для дать несколько иное представление. Используя уравнение, которое утверждает

12.14 A1v¯1=A2v¯2,A1v¯1=A2v¯2, размер 12{A rSub { размер 8{1} } {над чертой {v rSub { размер 8{1} } }} = A rSub { размер 8{2} } {overline {v rSub { размер 8{2} } }} } {}

решение для v¯2v¯2 размер 12{ {overline {v rSub {размер 8{2} } } } } {} и подставив πr2πr2 size 12{πr rSup { size 8{2} } } {} вместо площади поперечного сечения, получим

12. 15 v¯2=A1A2v¯1=πr12πr22v¯1=r12r22v¯1.v¯2=A1A2v¯1=πr12πr22v¯1=r12r22v¯1. size 12{ {overline {v rSub { size 8{2} } }} = { {A rSub { size 8{1} } } over {A rSub { size 8{2} } } } {overline {v rSub { size 8{1} } }} = { {πr rSub { размер 8{1} rSup { размер 8{2} } } } над {πr rSub { размер 8{2} rSup { размер 8{2} } } } } { overline {v rSub { размер 8{1} } }} = { {r rSub { размер 8{1} rSup { размер 8{2} } } } над {r rSub { размер 8{2} rSup { размер 8{2 } } } } } {overline {v rSub { size 8{1} } }} } {}

Замена известных значений,

12.16 v¯2=(0,900 см)2(0,250 см)21,96 м/с=25,5 м/с. v¯2=(0,900 см)2(0,250 см)21,96 м/с=25,5 м/с. size 12{ {overline {v rSub { size 8{2} } }} = { { \( 0 “.” “900”” cm” \) rSup { size 8{2} } } over { \( 0 “. ” “250”” см” \) rSup {размер 8{2} } } } 1 “.” “96”” м/с”=”25″ “.” “5 м/с”} {}

Обсуждение

Скорость 1,96 м/с подходит для воды, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Выполнение соединений: трубы разного размера

Для несжимаемых жидкостей плотность жидкости остается постоянной на всем протяжении, независимо от скорости потока или размера отверстия, через которое протекает жидкость. Мы говорим, что для обеспечения непрерывности потока количество жидкости, протекающей мимо любой точки, является постоянным. Это количество может быть измерено либо по объему, либо по массе.

Скорость потока выражена в единицах объема/времени (м ³ /с или л/с). Массовый расход (ΔmΔt)(ΔmΔt) выражен в единицах массы/времени (кг/с) и может быть рассчитан по расходу с использованием плотности.

Средний массовый расход можно найти по расходу.

12.18 ΔmΔt=mt= ρVt= ˙ρQ=ρAvΔmΔt=mt= ρVt= ˙ρQ=ρAv

Предположим, что сырая нефть плотностью 880 кг/м ³ течет по трубе диаметром 55 см со скоростью 1,8 м/с. Рассчитайте новую скорость сырой нефти, когда труба сузится до нового диаметра 31 см, и рассчитайте массовый расход в обеих секциях трубы, предполагая, что плотность нефти постоянна по всей трубе.

Раствор

Для расчета новой скорости мы просто используем уравнение непрерывности.

Поскольку поперечное сечение трубы представляет собой круг, площадь каждого поперечного сечения можно найти следующим образом:

Для большей трубы

12.19 A1= π(d12)2= π(0,275)2=0,238 м2. A1= π(d12)2= π(0,275)2=0,238 м2.

Для меньшей трубы

12,20 A2=π(0,155)2= 0,0755 м2.A2=π(0,155)2= 0,0755 м2.

Таким образом, большая часть трубы ( A ₁ ) имеет площадь поперечного сечения 0.238 м ² , а меньшая часть трубы ( А ₂ ) имеет площадь поперечного сечения 0,0755 м ² . Уравнение неразрывности говорит нам о том, что масло будет течь быстрее по участку трубы с меньшей площадью поперечного сечения. Используя уравнение неразрывности, получаем

12.21 А1в1= А2в2А1в1= А2в2 12,22.

Итак, мы находим, что масло течет со скоростью 1.8 м/с через большее сечение трубы ( A ₁ ), а через меньшее сечение ( A ₂ ) он течет намного быстрее (5,7 м/с).

Массовый расход в обеих секциях должен быть одинаковым.

Для большей части трубы

12,23 (ΔmΔt)1= ρA1v1=(880)(0,238)(1,8)= 380 кг/с. (ΔmΔt)1= ρA1v1=(880)(0,238)(1,8)= 380 кг/с.

Для меньшей части трубы

12,24 (ΔmΔt)2= ρA2v2=(880)(0,0755)(5,7)= 380 кг/с.(ΔmΔt)2= ρA2v2=(880)(0,0755)(5,7)= 380 кг/с.

Таким образом, масса трубы сохраняется. Каждую секунду из большей части трубы вытекает 380 кг нефти, а в меньшую — 380 кг нефти.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии, называемые артериолами, которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид

12.25 n1A1v¯1=n2A2v¯2,n1A1v¯1=n2A2v¯2, размер 12{n rSub { размер 8{1} } A rSub { размер 8{1} } {зачеркнутый {v rSub {размер 8{1}} }} =n rSub { размер 8{2} } A rSub { размер 8{2} } {перечеркнутый {v rSub { размер 8{2} } }} } {}

, где n1n1 размер 12{n rSub { размер 8{ 1} } } {} и n2n2 size 12{n rSub { size 8{2} } } {} — количество ответвлений на каждом из участков вдоль трубы.

Пример 12.3 Расчет скорости потока и диаметра сосуда: разветвление в сердечно-сосудистой системе

Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу.а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра равен 8 мкм, рассчитайте количество капилляров в системе кровообращения.

Стратегия

Мы можем использовать Q=Av¯Q=Av¯ размер 12{Q=A {overline {v}} } {} для расчета скорости потока в аорте, а затем использовать общую форму уравнения непрерывности для расчета количество капилляров, поскольку все остальные переменные известны.

Раствор для (а)

Расход определяется как Q=Av¯Q=Av¯ размер 12{Q=A {над чертой {v}} } {} или v¯=Qπr2v¯=Qπr2 размер 12{ {над чертой {v}} = { { Q} над {πr rSup {размер 8{2} } } } } {} для цилиндрического сосуда.

Подстановка известных значений (в пересчете на метры и секунды) дает

12,26 v¯ знак равно 5 л/мин 10 − 3 м 3 /л 1 мин/ 60 с π 0 . 010 м 2 знак равно 0 . 27 РС .v¯ знак равно 5 л/мин 10 − 3 м 3 /л 1 мин/ 60 с π 0 . 010 м 2 знак равно 0 .27 РС . размер 12{ { бар {v}}= { { левый (5 “.” 0`”л/мин” правый ) левый (“10” rSup { размер 8{- 3} } `m rSup { размер 8{3} } “/L” вправо ) влево (1`”мин/””60″`s вправо )} более {π влево (0 “.” “010 м” вправо ) rSup { размер 8{2} } } } =0 “.” “27”`”м/с”} {}

Решение для (b)

Используя n1A1v¯1=n2A2v¯1n1A1v¯1=n2A2v¯1 size 12{n rSub { size 8{1} } A rSub { size 8{1} } {overline {v rSub { size 8{1} } }} =n rSub { size 8{2} } A rSub { size 8{2} } {overline {v rSub { size 8{2} } }} } {}, присвоение нижнего индекса 1 к аорте и 2 к капиллярам, ​​и решение для размера n2n2 12{n rSub {размер 8{2} } } {} (количество капилляров) дает n2=n1A1v¯1A2v¯2n2=n1A1v¯1A2v¯2. Преобразование всех величин в единицы метров и секунд и подстановка в приведенное выше уравнение дает

12,27. н 2 знак равно 1 π 10 × 10 − 3 м 2 0,27 м/с π 4 × 10 − 6 м 2 0.33 × 10 − 3 РС знак равно 5,0 × 10 9 капилляры . н 2 знак равно 1 π 10 × 10 − 3 м 2 0,27 м/с π 4 × 10 − 6 м 2 0. 33 × 10 − 3 РС знак равно 5,0 × 10 9 капилляры . размер 12 {n rSub { размер 8 {2} } = { { левый (1 правый) левый (π правый) левый (“10” умножить на “10” rSup { размер 8 {- 3} } “m” правый) rSup { размер 8 {2} } влево (0 “.” “27” “м/с” вправо)} над { влево (π вправо) влево (4 “.” 0 раз “10” rSup { размер 8 {- 6} } ” m” справа ) rSup { размер 8 {2} } слева (0 “.” “33” умножить на “10” rSup {размер 8{ – 3} } “м/с” вправо )} } =5 “.” 0 раз “10” rSup {размер 8{9} } “капилляры”} {}

Обсуждение

Обратите внимание, что скорость кровотока в капиллярах значительно снижена по сравнению со скоростью в аорте из-за значительного увеличения общей площади поперечного сечения капилляров. Эта низкая скорость должна дать достаточно времени для эффективного обмена, хотя не менее важно, чтобы поток не становился стационарным, чтобы избежать возможности свертывания крови. Кажется ли разумным такое большое количество капилляров в организме? В активной мышце можно найти около 200 капилляров на мм3мм3 размером 12{“мм” rSup {размер 8{3} } } {}, или около 200×106200×106 размер 12{“200” умножить на “10” rSup {размер 8 {6} } } {} на 1 кг мышц. Для 20 кг мышц это составляет примерно 4×1094×109 капилляров размером 12{4, умноженных на “10” rSup {размер 8{9} } } {}.

Соединения: шприцы

Горизонтально ориентированный шприц для подкожных инъекций имеет диаметр цилиндра 1.2 см и диаметром иглы 2,4 мм. Плунжер выталкивает жидкость в цилиндр со скоростью 4 мм/с. Рассчитайте скорость потока жидкости в обеих частях шприца (в мл/с) и скорость жидкости, выходящей из иглы.

Раствор

Сначала рассчитайте площадь обеих частей шприца.

12.28 A1= π(d12)2= π(0,006)2= 1,13 × 10−4 м2A1= π(d12)2= π(0,006)2= 1,13×10−4 м2 12.29 A2= π(d22)2= π(0,0012)2= 4,52 × 10−6 м2A2= π(d22)2= π(0,0012)2= 4,52×10−6 м2

Затем мы можем использовать уравнение неразрывности, чтобы найти скорость жидкости в меньшей части бочки ( v ₂ ).

12.30 A1v1= A2v2A1v1= A2v2 12.31 v2= (A1A2)v1v2= (A1A2)v1 12,32 v2= (1,13×10−44,52×10−6)(0,004)= 0,10 м/сv2= (1,13×10−44,52×10−6)(0,004)= 0,10 м/с Убедитесь, что скорость потока в обеих частях шприца одинакова.

12,33 Q1= A1v1=(1,13×10-4)(0,004)= 4,52×10-7 м3/сQ1= A1v1=(1,13×10-4)(0,004)= 4,52×10-7 м3/с12,34 Q2= A2v2=(4,52×10-6)(0,10)= 4,52×10-7 м3/сQ2= A2v2=(4,52×10-6)(0,10)= 4,52×10-7 м3/с

Наконец, путем преобразования в мл /с.

12.35 (4,52×10-7 м31с)(106мл1м3)=0,452мл/с(4,52×10-7м31с)(106мл1м3)=0,452мл/с

Уравнение и формула массового расхода | Уравнение объемного расхода — видео и расшифровка урока

Уравнение массового расхода

Уравнение массового расхода можно легко вывести, просто просмотрев определение массового расхода и вспомнив его стандартную единицу измерения. Единицами массового расхода являются кг/с, масса за время, что указывает на то, что массовый расход представляет собой отношение изменения массы жидкости к изменению во времени . Ниже представлена ​​формула массового расхода :

{eq}\dot{m}=dm/dt {/eq}

Где {eq}dm {/eq} — изменение массы, {eq}dt {/eq} — изменение времени, а {eq}\dot{m} {/eq} — массовый расход. Точка над m используется для различения обычной массы m и массового расхода.

Отношение массового расхода к объемному расходу

Объемный расход , часто называемый объемным расходом , представляет собой объем жидкости, проходящий через площадь поперечного сечения за время.

Как массовый, так и объемный расход связаны друг с другом точно так же, как масса и объем связаны друг с другом. В некотором смысле массовый расход — это мера количества жидкости, протекающей, скажем, по трубе, а объемный расход — это мера трехмерного пространства, занимаемого жидкостью, проходящей через трубу.

Отношение массы к объему дает плотность. Использование этого соотношения является ключом к преобразованию массового расхода в объемный:

{eq}Q=\frac{\dot{m}}{\rho } {/ eq}

Преобразование объемного расхода в массовый расход:

{eq}\dot{m}=Q*\rho {/eq}

Примечание: Q объемный расход

Как Рассчитать массовый расход?

Приведенные примеры покажут, как рассчитать массовый расход:

• Пример 1: Вода наливается в бак емкостью 80 {экв}м^3 {/экв}, заполняя его до краев. 3 {/экв}).

{экв}м = v * \rho = 80 * 1000 = 80000 кг {/экв}

{экв}\точка{м}=м/т = 80000/2 = 40000 \фрак{кг}{ч} *\frac{1hr}{3600s}=11,1\frac{kg}{s} {/eq}

• Пример 2. Когда из цилиндра сливают 400 г воды, в цилиндре остается 200 г воды. г. Найдите массовый расход, если время в этом процессе 60 секунд.

{eq}\dot{m}=dm/dt = (m_2 – m_1)/(t_2 – t_1) = (200 – 400)/(60 – 0)=-3,33\frac{kg}{s} { /экв}

Массовый расход воды равен (-)3.33 кг/с. Знак минус указывает на то, что вода выходит из системы. Положительный массовый расход означает, что он поступает в систему.

Уравнение объемного расхода

Уравнение объемного расхода , относящееся к скорости потока: , v — скорость жидкости, а A — площадь поперечного сечения, через которое проходит жидкость.3/s] {/eq} кубических метров в секунду . Если задано значение массового расхода, объемный расход можно вычислить, просто разделив массовый расход на плотность жидкости, как показано в предыдущем разделе.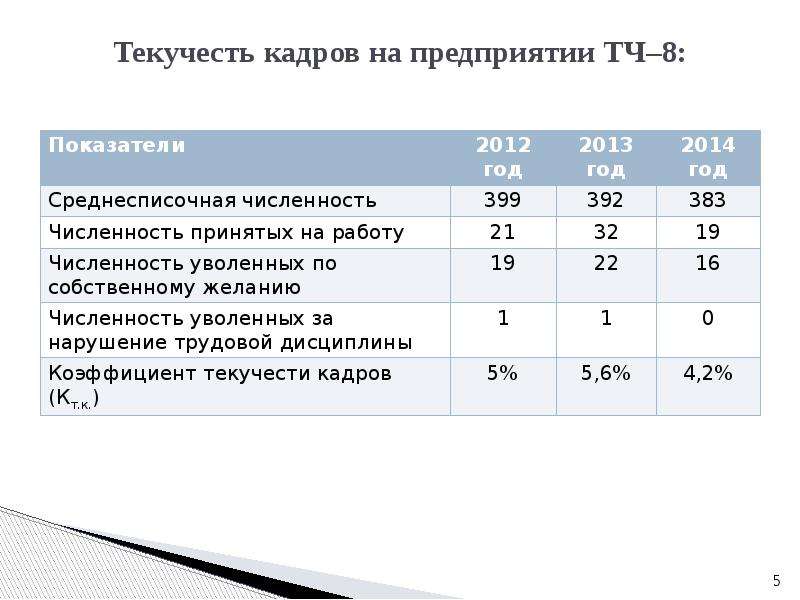 3{/экв}.3/с = 20,6 кг/с {/eq}

Отношение массового расхода к скорости

Скорость жидкости связана с массовым расходом через уравнение объемного расхода. Поскольку:

{eq}\dot{m}=Q*\rho {/eq}

и {eq}Q = v * A {/eq}

, тогда {eq}\dot{m}=(v * A)*\rho {/eq}.

Приведенный пример покажет, как можно рассчитать скорость по заданному массовому расходу:

Пример: Скорость по массовому расходу

Вода течет по круглой трубе, радиус которой равен 1.2 {/eq}

Массовый расход: {eq}\dot{m}=Q* \rho = 0,056*998 = 55,88 кг/с {/eq}.

Скорость воды: {eq}v = \dot{m}/(\rho * A)= 55,88/(998*0,000706) = 79,3 м/с {/eq}

Уравнение непрерывности Жидкости

Это учитывая тот факт, что ни масса, ни энергия не могут быть созданы или уничтожены, и то же самое относится к жидкостям, проходящим через трубопроводы. Количество, входящее в трубу, равно количеству, выходящему из нее, что является принципом сохранения массы . В этом случае это называется уравнением непрерывности . Прежде чем продолжить обсуждение этого уравнения, следует отметить, что такие жидкости, как упоминалось выше, являются идеальными жидкостями , и они подпадают под следующие предположения:

• Жидкости несжимаемы, что верно для жидкостей, но не для газов, но для простоты предполагается, что все жидкости несжимаемы.
• Жидкости снова демонстрируют сопротивление, поток считается незначительным, то есть жидкости невязкие .
• Частицы жидкости движутся плавно и равномерно, без колебаний. Другими словами, жидкость ламинарна .

Течение жидкости: сравнение ламинарного течения (а) и турбулентного течения (б)

Предположение о несжимаемости жидкостей упрощает ситуацию, так что объемный расход в любой заданной точке сегмента трубы такой же, как и в остальных точках.

Вывод уравнения неразрывности

Вывод уравнения неразрывности упрощается, если вспомнить, что объемный расход — это объем жидкости, проходящий через определенную точку сегмента трубы в единицу времени {eq}Q = V/t {/eq} , это можно использовать как отправную точку для вывода.

Вывод уравнения неразрывности

Уравнение неразрывности утверждает, что количество жидкости в точке x в трубе должно быть таким же в точке y в трубе.На изображении выделены два поперечных сечения, 1 и 2, что свидетельствует о том, что масса жидкости сохраняется и связана с объемом через плотность; можно сказать, что:

{eq}\dot{m_1}=\dot{m_2} {/eq}

{eq}Q_1 \rho = Q_2 \rho \rightarrow Q_1 = Q_2 {/eq} (плотность получает отменено, так как это одно и то же значение как в правой, так и в левой части уравнения.)

Поток жидкости через сегмент 1: {eq}Q_1 = V_1/t {/eq}

Объем цилиндра {eq} V = A * L {/eq}, поэтому {eq}Q_1 = (A_1 * L_1)/t {/eq}. Скорость равна длине (перемещению), деленной на время {eq}v = L / t {/eq}, что составляет:

{eq}Q_1 = A_1 \frac{L_1}{t} = A_1 * v_1 {/eq }.

Повторение того же процесса во втором сегменте дает {eq}Q_2 = A_2 * v_2 {/eq}. Объем жидкости, протекающей через секцию 1, равен объему жидкости, протекающей через секцию 2, таким образом:

{eq}Q_1 = Q_2 \rightarrow A_1 * v_1 = A_2 * v_2 {/eq}

Сегмент трубы расширен, как показано на рисунке. Чтобы жидкость сохраняла свою массу при движении, как это диктуется принципом сохранения, скорость жидкости, приближающейся к участку 2, будет уменьшаться, так как площадь этого поперечного сечения увеличилась.Уравнение неразрывности показывает, что уменьшение площади поперечного сечения связано с увеличением скорости жидкости, так что количество жидкости, протекающей в точке x, такое же, как и в точке y.

Краткий обзор урока

Массовый расход является важной переменной в технике и механике жидкости, это количество жидкости, протекающей в единицу времени, и его единица СИ составляет кг/с .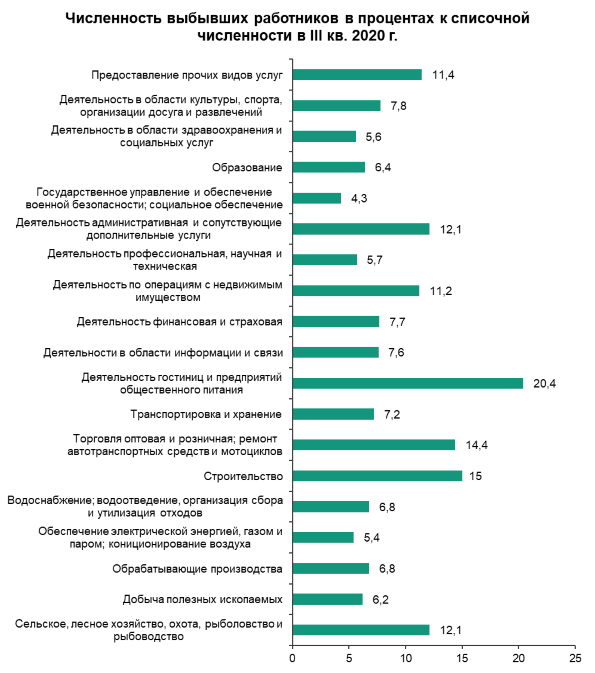 Формула массового расхода :

{eq}\dot{m}=dm/dt {/eq}

Объемный расход относится к трехмерному пространству, занимаемому жидкостью, протекающей через поперечное сечение за раз.Это отношение изменения объема протекающей жидкости к изменению во времени. Это связано с массовым расходом так же, как связаны обычная масса и объем; их соотношение с плотностью можно использовать для преобразования массового расхода в объемный. Для определения объемного расхода используются следующие уравнения:

• {экв} Q = \frac{\dot{m}}{\rho} {/экв}

Уравнение неразрывности основано на принципе сохранения массы , где количество втекающей жидкости должно быть таким же, как количество вытекающей.Жидкости, удовлетворяющие уравнению непрерывности:

• Ламинарная текут плавно и стабильно.
• Невязкие не обладают сопротивлением течению.
• Несжимаемые описываются как идеальные жидкости .

Уравнение неразрывности утверждает, что если поперечное сечение трубы уменьшается, скорость жидкости увеличивается, при условии, что скорость потока до и после сужения трубы одинакова. Как показано в формуле {eq}Q_1 = Q_2 \rightarrow A_1 * v_1 = A_2 * v_2 {/eq}.Скорость жидкости изменяется в зависимости от поперечного сечения сегмента таким образом, что количество жидкости, протекающей между каждой точкой, является однородным. Например, увеличивается скорость прохождения жидкости через узкий отрезок.

Самый быстрый словарь в мире | Vocabulary.com

скорость потока Количество жидкости, протекающей в данный момент времени

блок-схема диаграмма, показывающая последовательность операций или ход процесса или системы

блок-схема схема, показывающая последовательность операций или прогрессию

76″>

цветок миниатюрный цветок

сложный, отличающийся сложностью и богатством деталей

фильтрат продукт фильтрации

витиеватые, искусно или чрезмерно украшенные

цветки, напоминающие цветы, состоящие из них или напоминающие цветы

соцветие миниатюрный цветок

совместная работа над общим предприятием или проектом

головка цветка укороченное компактное соцветие, расположенное таким образом, что все вместе создает эффект одиночного цветка, как у клевера или представителей семейства сложноцветных

17″>

неграмотный не умеет читать и писать

напольные с полом

Флорида штат на юго-востоке США между Атлантикой и Мексиканским заливом; один из штатов Конфедерации во время Гражданской войны в США

преднамеренный, тщательно продуманный заранее

флокулируют в агрегированную комковатую или рыхлую массу

Viola odorata Европейская фиалка, обычно с цветками от пурпурных до белых

затвор клапан, регулирующий поток воды

Тис флоридский небольшой кустистый тис из северной Флориды с раскидистыми ветвями и очень узкими листьями

41″>

терпеть терпеть что-то или кого-то неприятное

Расход (объем) — обзор

7.5.5.2 Линейный источник

Для линейного источника Mundt ²⁴¹ приводит следующие формулы подъема шлейфа: Высота равновесия:

(7,228)zt=0,35Φ1/3(dθdz)−1/2

Объемный расход:

•

5 вычислить 1 высоту и положение источника

над виртуальным источником.

•

Для высоты z над виртуальным источником вычислить z ₁ :

(7.229)z1=5,78z(dθ/dz)1/2Φ−1/3

Если 2,0< z ₁ < 2,95, то разность плотностей исчезает и расчеты становятся неопределенными; если z ₁ ≥2,95, шлейф достиг максимальной высоты ниже фактического уровня.

•

9 •

расчет

(7.230) a = 0,004 + 0,477Z1 + 0,029z12-0,018z13

•

•

Расход объема задается на

(7. 231) QV, 1 = 0,00482φ2 /3(dθ/dz)−1/2a

где

q _{v ,1} объемный расход в м ³ /с м.

Пример 7.5.5

Точечный источник в помещении с термической стратификацией рис. 7.76). В этом случае мы предполагаем, что в помещении есть другие источники тепла. Мы хотим исследовать, как эта температурная стратификация влияет на объемный поток в факеле над цилиндром и на какой высоте факел останавливается.

Рисунок 7.76. Цилиндр примера 7.5.4 в помещении с термической стратификацией.

Следуя формулам и процедуре расчета раздела 7.5.5.1, получаем

1.

Местоположение виртуального источника: используем местоположение, рассчитанное для максимального случая в примере 7.5.4, т.е.

zp=–0,83м.

2.

Максимальный подъем шлейфа: максимальная высота над виртуальным источником находится из уравнения. (7.222):

zmax=0,98×50001/4×1,5–3/8=7,08м,

т.е. максимальная высота 7,08м над виртуальным источником, что составляет

7,08м–0,83м=6,25м над полом

Высота равновесия (уравнение 7.223):

zt=0,74×50001/4×1,5–3/8=5,34 м,

, то есть равновесная или конечная высота составляет 5,34 м над виртуальным источником, что равно

5,34–0,83 = 4,51 м над полом.

3.

Объемный расход в шлейфе: найти объемный расход воздуха через уровень z _этаж =3.5 м, мы должны сначала вычислить z , а затем z ₁ на этом уровне с помощью уравнения (7.224):

z1=2,86×(3,5+0,83)×1,53/85000–1/4=1,715

С z ₁ мы можем вычислить 6 m 1 по уравнению

(7.225):

м1=0,004+0,039z1+0,380z12−0,062z13=0,875,

, что дает скорость конвекционного воздушного потока из уравнения (7.226):

qv=0,00238×(50003/4)×1,5–5/8×0,875=0,96 м3/с.

Расчетный объемный расход 3.5 м над полом немного ниже расчетного для изотермической атмосферы. Отклонение между объемными расходами, рассчитанными для изотермического комнатного воздуха и стратифицированного комнатного воздуха, можно увидеть на рис. 7.77.

Пример 7.5.6

Сравнение с численным моделированием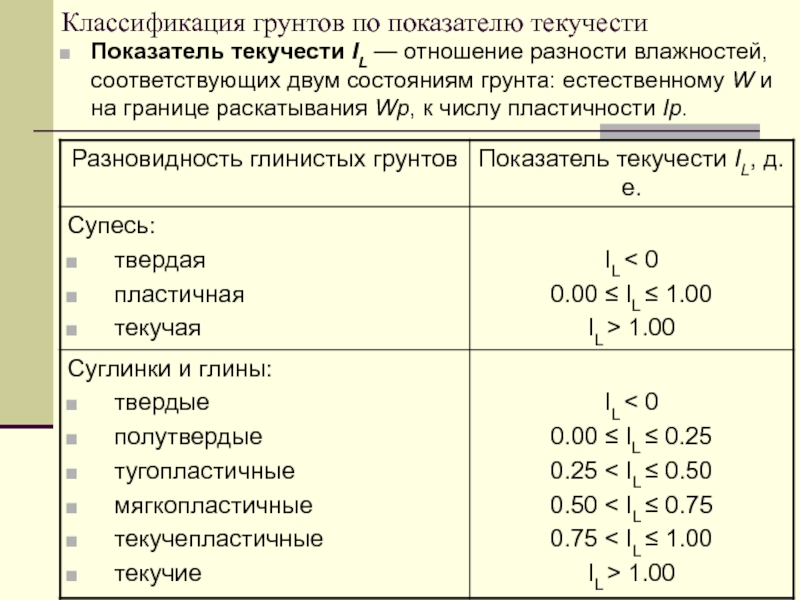

Рисунок 7.77. Расход воздуха в факеле над цилиндром Примера 7.5.5.

Рассчитать максимальную скорость воздуха, расход воздуха и избыточную температуру (относительно температуры окружающего воздуха, равной 20°С) в тепловом шлейфе над нагретым кубом (0.66 м×0,66 м×0,66 м) при конвективной теплопроизводительности Вт _усл =225 Вт, на высотах 2,0 и 4,0 м над уровнем пола. Градиентом температуры по высоте помещения пренебречь. Сравните результаты с прогнозами, сделанными для того же случая с использованием кода CFD ²⁷³ (рис. 7.78).

Рисунок 7.78. Предсказываемые CDF значения максимальной скорости V , перепада температур θ _max (°C) и расхода воздуха q (л/с) в горизонтальном сечении плавучего факела над нагретым куб (0. 66 м × 0,66 м × 0,66 м, 225 Вт). ²⁷³

Для расчета теплового шлейфа куб можно представить в виде цилиндра с диаметром, эквивалентным гидравлическому диаметру вершины куба:

D=4×0,66×0,664×0,66=0,66м.

В минимальном случае

zo=0,8D/(2tan12,5°)=1,19м.

Виртуальный источник расположен ниже уровня пола:

zp=D/3+H–zo=0,66/3+0,66–1,19=–0,31м.

Таким образом, вертикальные расстояния, используемые при расчете характеристик шлейфа, соответственно равны 2.31 и 4,31 м.

Максимальная скорость в тепловом шлейфе, из табл. 7.19, равна 3⋅4,31–1/3=0,48 м/с.

Соответствующие значения максимальных скоростей в шлейфе на высотах 2,0 и 4,0 м над уровнем пола, из таблицы на рис. 7.78, равны 0,54 и 0,42 м/с.

Максимальная избыточная температура в тепловом шлейфе, по таблице 7.19, составляет

Δθ=0,329×2252/3×2,31–5/3=3.0°С

и

Δθ=0,329×2252/3×4,31–5/3=1,06°С.

Соответствующие значения максимальных избыточных температур в шлейфе на высотах 2,0 и 4,0 м над уровнем пола, из таблицы на рис. 7.78, составляют 3,6°С и 1,06°С.

Максимальный расход воздуха в тепловом шлейфе по таблице 7.19 составляет

qv,z=0,005×2251/3×2,315/3=0,123 м3с и

qv,Z=0,005×2251/3×4,315/3= 0,347м3с.

Соответствующие значения расходов воздуха в факеле на высотах 2.0 и 4,0 м над уровнем пола, из таблицы на рис. 7.78, составляют 0,18 и 0,35 м ³ /с.

Существует очень хорошее соответствие между аналитическими и численными результатами для температуры и скорости. Однако скорости воздушного потока различаются в 1,46 раза на высоте 2 м, тогда как соответствие на высоте 4 м очень хорошее.

Расход жидкости – обзор

12.3.3 Взаимосвязь между давлением и расходом

Расход жидкости-носителя пульпы, u _{л , может быть выражен через давление выходящей жидкости, 5 e}

p p p p (атм), на выходе из пористого пласта, давление, p _c (атм), на поверхности корки со стороны шлама и гармоническая средняя проницаемость корки и пласта.

Закон Форхгеймера (1901) о течении через пористую среду для линейного случая определяется как: путем интегрирования уравнения (12.133), соответственно, как (Civan, 1999c):

(12.134)pc−pw=[µK¯cu¯c+ρcβ¯cu¯c2](xw−xc)

(12.135)pw−pe=[ µK¯fu¯f+ρfβ¯fu¯f2](xe−xw)

Мгновенные объемные потоки и плотности взвесей мелких частиц, протекающих через матрицу корки и пористую формацию, предполагаются одинаковыми.Затем, добавляя уравнения. (12.134) и (12.135), а также перестановка и решение дают (Civan, 1999c) для потока Дарси (βf=βc=0):

(12.136)u¯c=u¯f≅uc=−γ˜/β ˜

и для потока, отличного от Дарси:

(12,137)u¯c=u¯f≅uc=(ul)slurry1−(εpl)slurry=−β˜+β˜2−4α˜γ˜2α˜

, в котором:

(12.138)α˜=ρ[β¯c(xw−xc)+βf(xe−xw)]

(12.139)β˜=µ[xw−xcK¯c+xe−xwK¯ f]

(12,140)γ˜=-(pc−pe)

Хотя предыдущий подход дает достаточно хорошую точность, более строгая обработка должна облегчить:

(12.141)uc=u¯c−(xw−xc)du¯cdxc

Закон Форхгеймера (1901 г. ) для случая радиального течения имеет вид: поток и расход связаны соотношением:

(12,143)u=q2πrh

, где ч – мощность пласта. Таким образом, вызывая уравнение (12.143) в уравнение (12.142) дает:

(12,144)−∂p∂r=μ2πhK(qr)+ρβ(2πh)2(qr)2

Разность давлений над фильтрационной коркой и пористой средой может быть выражена путем интегрирования уравнения(12.144), соответственно, как (Civan, 1999c):

(12.145)pc−pw=µq¯c2πhK¯cln(rwrc)+ρβ¯cq¯2(2πh)2(1rc−1rw)

(12.146) pw−pe=µq¯f2πhK¯fln(rerw)+ρβ¯fq¯f2(2πh)2(1rw−1re)

предполагается одинаковым. Затем, добавляя уравнения. (12.145) и (12.146), а также обратное ранжирование и решение дают (Civan, 1999c) для потока Дарси (βf=βc=0):

(12,147)q¯c=q¯f≅qc=−γ˜/ β˜

и для потока не Дарси:

(12.148)q¯c=q¯f≅qc=uc2πrch=(ul)slurry2πrch[1−(εpl)slurry]=−β˜+β˜2−4α˜γ˜2α˜

в котором:

(12,149 )α˜=ρ(2πh)2[β¯c(1rc−1rw)+βf(1rw−1re)]

(12,150)β˜=µ2πh[1K¯cln(rwrc)+1K¯fln(rerw)]

(12,151)γ˜=−(pc−pe)

Хотя этот подход дает достаточно хорошую оценку, следует использовать более строгий подход:

(12,152)qc=q¯c−[rw2−rc22rc]dq ¯cdrc

Коэффициент инерционного потока оценивается Liu et al.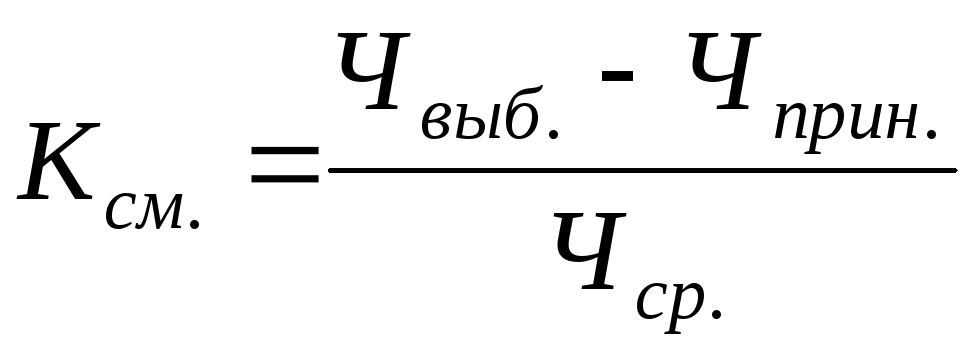 (1995) корреляция, заданная уравнением.(12.16).

Массовый расход

Массовый расход

Исследовательский центр Гленна

Сохранение массы является фундаментальным понятие физики. В некоторой проблемной области количество массы остается постоянным — масса не создается и не уничтожается. То масса любого объекта – это просто объем, который объект занимает раз больше плотности объекта.Для жидкости (жидкость или газ) плотность, объем и форма объекта могут изменяться в пределах домен со временем. И масса может двигаться через домен. На На рисунке показано течение газа через суженную трубку.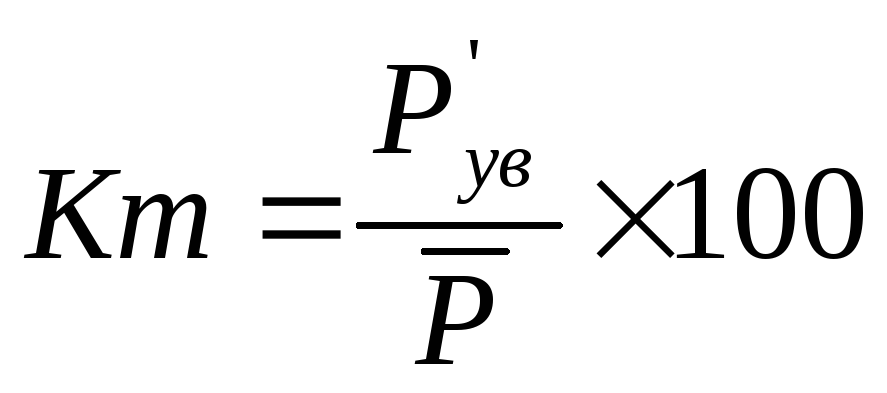 Здесь нет накопление или разрушение массы через трубку; То же количество массы покидает трубку, когда входит в трубку. В любом самолете перпендикулярно центральной линии трубы, такое же количество массы проходит через. Мы называем количество массы, проходящей через плоскость массовый расход . сохранение массы (непрерывность) говорит нам, что массовый расход через трубку равен постоянный. Мы можем определить значение массового расхода из условия течения.

Если жидкость первоначально проходит через площадь A со скоростью V , мы можем определить объем массы, который должен быть выметен за некоторое время т . Том v это:

v = А * V * т

Проверка единиц дает площадь x длина/время x время = площадь x длина = объем.Масса м содержится в этот объем просто плотность х раз больше объема.

м = г * А * V * т

Для определения массового расхода mточка делим масса к тому времени. Полученное определение массового расхода: показано на слайде красным цветом.

mточка = г * А * В

Как инженеры используют эти знания о массовом расходе? От Второй закон движения Ньютона, аэродинамических сил на самолете (подъемная и перетаскивание) напрямую связаны с изменением импульса газа со временем.То импульс определяется как масса, умноженная на скорость, поэтому мы можно было бы ожидать, что аэродинамические силы будут зависеть от массового расхода мимо объекта. Тяга, создаваемая двигательная установка также зависит от изменения количества движения рабочего газа. Тяга напрямую зависит от массы скорость потока через двигательную установку. Для течения в трубе масса скорость потока постоянна. Для потока с постоянной плотностью, если мы можем определить (или задать) скорость в некоторой известной области, уравнение сообщает нам значение скорости для любой другой области.Если мы желаем определенной скорости, мы знаем площадь, которую мы должны обеспечить для получить эту скорость.