Постановление 922 о расчете среднего: .15 N922 , , . 2021 , 01.07.2021 , ?
Учет премий в среднем заработке | «Правовест Аудит»
Для всех случаев определения размера среднего заработка, предусмотренных ТК РФ, установлен единый порядок его исчисления (ст. 139 ТК РФ, письмо от 05.07.2021 N 14-3/ООГ-6234). Для расчета среднего заработка учитываются все предусмотренные системой оплаты труда виды выплат, применяемые у соответствующего работодателя, независимо от источников выплат.
Виды выплат перечислены в п. 2 Положения об особенностях порядка исчисления средней заработной платы, утвержденного постановлением Правительства Российской Федерации от 24 декабря 2007 г. N 922 (далее — Положение), в том числе учитываются премии и вознаграждения, предусмотренные системой оплаты труда (пп «н» п. 2 Положения N 922), а также виды выплат по заработной плате, применяемые у соответствующего работодателя (пп.
Условия оплаты труда обязательны для включения в трудовой договор (ст. 57 ТК РФ). Если в трудовом договоре нет перечня стимулирующих выплат (премий) и порядка их начисления и выплаты, то должна быть ссылка на локальный акт организации, согласно которому начисляются и выплачиваются выплаты. Например: «Положение о премировании», «Положение о мотивации» и т.п.
Премия относится к разряду подлежащих или не подлежащих включению в расчет средней заработной платы не из-за периодичности или размера (фиксированного или динамичного), а в связи с результатами труда (выполнением трудовой функции).
Премия за производственные показатели, предусмотренная Положением о премировании (ином ЛНА), включается в систему оплаты труда и связана с результатами труда (ст. 135 ТК РФ). Следовательно, она входит в расчет среднего заработка.
Расчет среднего заработка работника независимо от режима работы производится исходя из фактически начисленной заработной платы и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя заработная плата. Календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале — по 28-е (29-е) число включительно) (ч. 3 ст. 139 ТК РФ, п. 4 Положения N 922)./p>
Календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале — по 28-е (29-е) число включительно) (ч. 3 ст. 139 ТК РФ, п. 4 Положения N 922)./p>
При определении среднего заработка учитываются вознаграждения по итогам работы за год, единовременное вознаграждение за выслугу лет, иные вознаграждения по итогам работы за год, начисленные за предшествующий событию календарный год, — независимо от времени начисления вознаграждения (абз. 4 п. 15 Положения N 922).
Если премии фактически начисляются за период больше года, например, по итогам работы четырех лет, то данная норма для расчета среднего заработка не применяется.
При определении среднего заработка премии и вознаграждения учитываются в следующем порядке: премии и вознаграждения за период работы более месяца (в данном случае за 4 года (48 месяцев)), —  3 п. 15 Положения N 922).
3 п. 15 Положения N 922).
Премия будет учитываться только если дата начисления попала в расчетный период для сохранения среднего заработка, а дата ее выплаты значения не имеет. Причем будет учитываться не в фактически начисленной сумме, а в месячной части. То есть начисленную сумму премии нужно разделить на 48 месяцев (4 года за которые она начислена) и умножить на 12 месяцев (расчетный период из которого исчисляется средний заработок).
Документы – Правительство России
ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПОСТАНОВЛЕНИЕ
от 7 июля 2021 г. № 1124
МОСКВА
Об утверждении Правил предоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели
Правительство Российской Федерации постановляет:
1. Утвердить прилагаемые Правила предоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели.
Утвердить прилагаемые Правила предоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели.
2. Установить, что выплаты стимулирующего характера, предусмотренные постановлением Правительства Российской Федерации от 2 апреля 2020 г. № 415 “Об утверждении Правил предоставления в 2020 году иных межбюджетных трансфертов из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования, в том числе в полном объеме, расходных обязательств субъектов Российской Федерации, возникающих при осуществлении выплат стимулирующего характера за особые условия труда и дополнительную нагрузку медицинским работникам, оказывающим медицинскую помощь гражданам, у которых выявлена новая коронавирусная инфекция, и лицам из групп риска заражения новой коронавирусной инфекцией” и постановлением Правительства Российской Федерации от 12 апреля 2020 г. № 484 “Об утверждении Правил предоставления в 2020 году иных межбюджетных трансфертов из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования в полном объеме расходных обязательств субъектов Российской Федерации, возникающих при осуществлении выплат стимулирующего характера за выполнение особо важных работ медицинским и иным работникам, непосредственно участвующим в оказании медицинской помощи гражданам, у которых выявлена новая коронавирусная инфекция COVID-19”, учитываются в расчете средней заработной платы для оплаты отпусков и выплаты компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году такие выплаты предоставлялись.
№ 415 “Об утверждении Правил предоставления в 2020 году иных межбюджетных трансфертов из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования, в том числе в полном объеме, расходных обязательств субъектов Российской Федерации, возникающих при осуществлении выплат стимулирующего характера за особые условия труда и дополнительную нагрузку медицинским работникам, оказывающим медицинскую помощь гражданам, у которых выявлена новая коронавирусная инфекция, и лицам из групп риска заражения новой коронавирусной инфекцией” и постановлением Правительства Российской Федерации от 12 апреля 2020 г. № 484 “Об утверждении Правил предоставления в 2020 году иных межбюджетных трансфертов из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования в полном объеме расходных обязательств субъектов Российской Федерации, возникающих при осуществлении выплат стимулирующего характера за выполнение особо важных работ медицинским и иным работникам, непосредственно участвующим в оказании медицинской помощи гражданам, у которых выявлена новая коронавирусная инфекция COVID-19”, учитываются в расчете средней заработной платы для оплаты отпусков и выплаты компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году такие выплаты предоставлялись.
3. Настоящее постановление вступает в силу со дня его официального опубликования.
Председатель ПравительстваРоссийской Федерации М.Мишустин
УТВЕРЖДЕНЫпостановлением ПравительстваРоссийской Федерацииот 7 июля 2021 г. № 1124
ПРАВИЛАпредоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели
1. Настоящие Правила устанавливают цели, порядок и условия предоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели (далее соответственно – выплаты стимулирующего характера, медицинские работники, иные межбюджетные трансферты).
Настоящие Правила устанавливают цели, порядок и условия предоставления в 2021 году иных межбюджетных трансфертов, имеющих целевое назначение, из федерального бюджета бюджетам субъектов Российской Федерации, источником финансового обеспечения которых являются бюджетные ассигнования резервного фонда Правительства Российской Федерации, в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой отпусков и выплатой компенсации за неиспользованные отпуска медицинским и иным работникам, которым в соответствии с решениями Правительства Российской Федерации в 2020 году предоставлялись выплаты стимулирующего характера за выполнение особо важных работ, особые условия труда и дополнительную нагрузку, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели (далее соответственно – выплаты стимулирующего характера, медицинские работники, иные межбюджетные трансферты).
2. Иные межбюджетные трансферты предоставляются бюджетам субъектов Российской Федерации в пределах лимитов бюджетных обязательств, доведенных в установленном порядке до Министерства здравоохранения Российской Федерации как получателя средств федерального бюджета на предоставление иных межбюджетных трансфертов на цели, указанные в пункте 1 настоящих Правил.
Иные межбюджетные трансферты предоставляются бюджетам субъектов Российской Федерации в пределах лимитов бюджетных обязательств, доведенных в установленном порядке до Министерства здравоохранения Российской Федерации как получателя средств федерального бюджета на предоставление иных межбюджетных трансфертов на цели, указанные в пункте 1 настоящих Правил.
3. Условием предоставления иных межбюджетных трансфертов является наличие в бюджете субъекта Российской Федерации бюджетных ассигнований на исполнение расходных обязательств субъектов Российской Федерации, в целях софинансирования которых предоставляются иные межбюджетные трансферты.
4. Критерием отбора субъектов Российской Федерации для предоставления иного межбюджетного трансферта является факт осуществления субъектом Российской Федерации в 2020 году в соответствии с решениями Правительства Российской Федерации выплат стимулирующего характера медицинским работникам.
5. Предоставление иных межбюджетных трансфертов осуществляется на основании соглашения о предоставлении иного межбюджетного трансферта, заключенного между Министерством здравоохранения Российской Федерации и высшим исполнительным органом государственной власти субъекта Российской Федерации (далее – соглашение) в форме электронного документа с использованием государственной интегрированной информационной системы управления общественными финансами “Электронный бюджет” в соответствии с типовой формой, утвержденной Министерством финансов Российской Федерации.
6. Результатом предоставления иного межбюджетного трансферта является количество дней, за которые в текущем финансовом году по 31 октября 2021 г. произведена оплата отпусков и выплата компенсации за неиспользованные отпуска медицинским работникам, которым в 2020 году в соответствии с решениями Правительства Российской Федерации предоставлялись выплаты стимулирующего характера.
7. Размер иного межбюджетного трансферта бюджету i-го субъекта Российской Федерации (Si) определяется по формуле:
Si = ((Vi / 12 / 29,3) x ki) – Ti,
где:
Vi – объем фактически осуществленных в 2020 году в соответствии с решениями Правительства Российской Федерации выплат стимулирующего характера медицинским работникам в i-м субъекте Российской Федерации по данным Федерального казначейства по состоянию на 1 января 2021 г.;
12 – количество месяцев, которое используется для расчета среднего дневного заработка для оплаты отпусков и выплаты компенсации за неиспользованные отпуска медицинским работникам в соответствии с постановлением Правительства Российской Федерации от 24 декабря 2007 г. № 922 “Об особенностях порядка исчисления средней заработной платы”;
№ 922 “Об особенностях порядка исчисления средней заработной платы”;
29,3 – среднемесячное число календарных дней, которое используется для расчета среднего дневного заработка для оплаты отпусков и выплаты компенсации за неиспользованные отпуска в соответствии с постановлением Правительства Российской Федерации от 24 декабря 2007 г. № 922 “Об особенностях порядка исчисления средней заработной платы”;
ki – среднее количество календарных дней отпуска медицинских работников в i-м субъекте Российской Федерации с учетом ежегодного дополнительного оплачиваемого отпуска за работу с вредными и (или) опасными условиями труда и ежегодного дополнительного оплачиваемого отпуска за работу в местностях с особыми климатическими условиями;
Ti – кассовый расход по иным межбюджетным трансфертам, предоставленным из федерального бюджета бюджетам субъектов Российской Федерации в 2020 году в соответствии с решениями Правительства Российской Федерации на цели, указанные в пункте 1 настоящих Правил, осуществленный с лицевого счета Министерства здравоохранения Российской Федерации, предназначенного для учета операций по переданным полномочиям получателя бюджетных средств, открытый в органе Федерального казначейства в i-м субъекте Российской Федерации, по состоянию на 1 января 2021 г.
Общий объем иных межбюджетных трансфертов бюджетам субъектов Российской Федерации определяется путем сложения размера иного межбюджетного трансферта (Si) каждого субъекта Российской Федерации, которому предоставляется иной межбюджетный трансферт.
8. При заключении соглашения высший исполнительный орган государственной власти субъекта Российской Федерации представляет в Министерство здравоохранения Российской Федерации отчет об исполнении условия предоставления иного межбюджетного трансферта.
9. Орган исполнительной власти субъекта Российской Федерации, уполномоченный высшим исполнительным органом государственной власти субъекта Российской Федерации, размещает в государственной интегрированной информационной системе управления общественными финансами “Электронный бюджет” по форме и в сроки, которые установлены соглашением:
а) отчет о расходах бюджета субъекта Российской Федерации, в целях софинансирования которых предоставляются иные межбюджетные трансферты;
б) отчет о достижении значения результата предоставления иного межбюджетного трансферта.
10. Иные межбюджетные трансферты предоставляются в целях софинансирования расходных обязательств субъектов Российской Федерации по финансовому обеспечению расходов, связанных с оплатой в соответствии с трудовым законодательством Российской Федерации отпусков и выплатой компенсации за неиспользованные отпуска медицинским работникам за период с начала осуществления в 2020 году выплат стимулирующего характера медицинским работникам в соответствии с решениями Правительства Российской Федерации по 31 октября 2021 г. включительно, в том числе на компенсацию ранее произведенных субъектами Российской Федерации расходов на указанные цели в 2021 году.
11. Перечисление иных межбюджетных трансфертов осуществляется в установленном порядке на единые счета бюджетов, открытые финансовым органам субъектов Российской Федерации в территориальных органах Федерального казначейства.
12. В случае нецелевого использования субъектом Российской Федерации бюджетных средств, источником софинансирования которых являются иные межбюджетные трансферты, к нему применяются бюджетные меры принуждения, предусмотренные бюджетным законодательством Российской Федерации.
13. Ответственность за достоверность представляемых в Министерство здравоохранения Российской Федерации информации и документов, предусмотренных настоящими Правилами, возлагается на высший исполнительный орган государственной власти субъекта Российской Федерации.
14. Контроль за соблюдением субъектами Российской Федерации целевого использования бюджетных средств, источником софинансирования которых являются иные межбюджетные трансферты, осуществляется Министерством здравоохранения Российской Федерации и уполномоченными органами государственного финансового контроля.
____________
Надо ли учитывать карантинные нерабочие дни при расчете средней зарплаты
Минтруд уточнил, надо ли учитывать нерабочие дни с 30 марта по 8 мая 2020 года, установленные президентскими указами, при расчете средней зарплаты работника. Соответствующие разъяснения даны в письме от 18.05.2020 № 14-1/В-585.
Ведомство напоминает, что порядок исчисления средней зарплаты установлен статьей 139 ТК РФ и Положением об особенностях порядка исчисления средней зарплаты, утвержденным правительственным постановлением от 24. 12.2007 № 922.
12.2007 № 922.
По указанному положению расчет среднего заработка работника независимо от режима его работы производится исходя из фактически начисленной ему зарплаты и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя зарплата.
При этом календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале – по 28-е (29-е) число включительно).
Данное положение (пункт 5) также устанавливает, что при исчислении среднего заработка из расчетного периода исключается время, а также начисленные за это время суммы, если:
а) за работником сохранялся средний заработок в соответствии с законодательством РФ, за исключением перерывов для кормления ребенка, предусмотренных трудовым законодательством;
б) работник получал пособие по временной нетрудоспособности или пособие по беременности и родам;
в) работник не работал в связи с простоем по вине работодателя или по причинам, не зависящим от работодателя и работника;
г) работник не участвовал в забастовке, но в связи с этой забастовкой не имел возможности выполнять свою работу;
д) работнику предоставлялись дополнительные оплачиваемые выходные дни для ухода за детьми-инвалидами и инвалидами с детства;
е) работник в других случаях освобождался от работы с полным или частичным сохранением заработной платы или без оплаты в соответствии с законодательством.
В связи с этим Минтруд считает, что время и суммы, фактически начисленные за нерабочий период с 30 марта по 8 мая 2020 года, при исчислении среднего заработка для случаев, предусмотренных ТК РФ, не учитываются.
Ведомство ссылается на указанный выше подпункт «е» пункта 5 положения об особенностях порядка исчисления средней зарплаты (правительственное постановление от 24.12.2007 № 922).
БУХПРОСВЕТ
Для расчета среднего заработка учитываются все предусмотренные системой оплаты труда виды выплат, применяемые у соответствующего работодателя, независимо от источников этих выплат. К таким выплатам относятся заработная плата, надбавки и доплаты к должностным окладам за профессиональное мастерство, классность, выслугу лет, выплаты, обусловленные районным регулированием оплаты труда.
Кроме того, при расчете среднего заработка учитывается повышенная оплата труда на тяжелых работах, работах с вредными или опасными условиями труда, надбавки за работу в ночное время, а также премии и вознаграждения, предусмотренные системой оплаты труда. Если работник не имел фактически начисленной заработной платы или отработанных дней за расчетный период, средний заработок определяется исходя из суммы зарплаты, начисленной за предшествующий период, равный расчетному.
Если работник не имел фактически начисленной заработной платы или отработанных дней за расчетный период, средний заработок определяется исходя из суммы зарплаты, начисленной за предшествующий период, равный расчетному.
Средний заработок определяется путем умножения среднего дневного заработка на количество дней в периоде, подлежащем оплате. Средний дневной заработок исчисляется путем деления суммы зарплаты, включая премии и вознаграждения, на количество фактически отработанных в этот период дней. Дневной заработок для оплаты отпусков исчисляется путем деления суммы зарплаты на 12 и на среднемесячное число календарных дней (29,3).
ПОСТАНОВЛЕНИЕ ПРАВИТЕЛЬСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ от 24 декабря 2007 г. N 922 ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПОСТАНОВЛЕНИЕ
от 24 декабря 2007 г. N 922
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
Список изменяющих документов
(в ред. Постановлений Правительства РФ от 11.11.2009 N 916,
Постановлений Правительства РФ от 11.11.2009 N 916,
от 25.03.2013 N 257, от 10.07.2014 N 642,
от 15.10.2014 N 1054, от 10.12.2016 N 1339)
В соответствии со статьей 139 Трудового кодекса Российской Федерации Правительство Российской Федерации постановляет:
1. Утвердить прилагаемое Положение об особенностях порядка исчисления средней заработной платы.
2. Министерству труда и социальной защиты Российской Федерации давать разъяснения по вопросам, связанным с применением Положения, утвержденного настоящим Постановлением.
(в ред. Постановления Правительства РФ от 25.03.2013 N 257)
3. Признать утратившим силу Постановление Правительства Российской Федерации от 11 апреля 2003 г. N 213 “Об особенностях порядка исчисления средней заработной платы” (Собрание законодательства Российской Федерации, 2003, N 16, ст. 1529).
Председатель Правительства
Российской Федерации
В.ЗУБКОВ
Утверждено
Постановлением Правительства
Российской Федерации
от 24 декабря 2007 г.
ПОЛОЖЕНИЕ
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
Список изменяющих документов
(в ред. Постановлений Правительства РФ
от 11.11.2009 N 916, от 10.07.2014 N 642,
от 15.10.2014 N 1054, от 10.12.2016 N 1339)
1. Настоящее Положение устанавливает особенности порядка исчисления средней заработной платы (среднего заработка) для всех случаев определения ее размера, предусмотренных Трудовым кодексом Российской Федерации (далее – средний заработок).
2. Для расчета среднего заработка учитываются все предусмотренные системой оплаты труда виды выплат, применяемые у соответствующего работодателя, независимо от источников этих выплат. К таким выплатам относятся:
а) заработная плата, начисленная работнику по тарифным ставкам, окладам (должностным окладам) за отработанное время;
б) заработная плата, начисленная работнику за выполненную работу по сдельным расценкам;
в) заработная плата, начисленная работнику за выполненную работу в процентах от выручки от реализации продукции (выполнения работ, оказания услуг), или комиссионное вознаграждение;
г) заработная плата, выданная в неденежной форме;
д) денежное вознаграждение (денежное содержание), начисленное за отработанное время лицам, замещающим государственные должности Российской Федерации, государственные должности субъектов Российской Федерации, депутатам, членам выборных органов местного самоуправления, выборным должностным лицам местного самоуправления, членам избирательных комиссий, действующих на постоянной основе;
е) денежное содержание, начисленное муниципальным служащим за отработанное время;
ж) начисленные в редакциях средств массовой информации и организациях искусства гонорар работников, состоящих в списочном составе этих редакций и организаций, и (или) оплата их труда, осуществляемая по ставкам (расценкам) авторского (постановочного) вознаграждения;
з) заработная плата, начисленная преподавателям профессиональных образовательных организаций за часы преподавательской работы сверх установленной и (или) уменьшенной годовой учебной нагрузки за текущий учебный год, независимо от времени начисления;
(в ред. Постановления Правительства РФ от 15.10.2014 N 1054)
Постановления Правительства РФ от 15.10.2014 N 1054)
и) заработная плата, окончательно рассчитанная по завершении предшествующего событию календарного года, обусловленная системой оплаты труда, независимо от времени начисления;
к) надбавки и доплаты к тарифным ставкам, окладам (должностным окладам) за профессиональное мастерство, классность, выслугу лет (стаж работы), знание иностранного языка, работу со сведениями, составляющими государственную тайну, совмещение профессий (должностей), расширение зон обслуживания, увеличение объема выполняемых работ, руководство бригадой и другие;
(в ред. Постановления Правительства РФ от 15.10.2014 N 1054)
л) выплаты, связанные с условиями труда, в том числе выплаты, обусловленные районным регулированием оплаты труда (в виде коэффициентов и процентных надбавок к заработной плате), повышенная оплата труда на тяжелых работах, работах с вредными и (или) опасными и иными особыми условиями труда, за работу в ночное время, оплата работы в выходные и нерабочие праздничные дни, оплата сверхурочной работы;
м) вознаграждение за выполнение функций классного руководителя педагогическим работникам государственных и муниципальных образовательных организаций;
(в ред. Постановления Правительства РФ от 15.10.2014 N 1054)
Постановления Правительства РФ от 15.10.2014 N 1054)
н) премии и вознаграждения, предусмотренные системой оплаты труда;
о) другие виды выплат по заработной плате, применяемые у соответствующего работодателя.
3. Для расчета среднего заработка не учитываются выплаты социального характера и иные выплаты, не относящиеся к оплате труда (материальная помощь, оплата стоимости питания, проезда, обучения, коммунальных услуг, отдыха и другие).
КонсультантПлюс: примечание.
О включении времени забастовки в расчетный период для исчисления среднего заработка см. письмо Минтруда РФ от 23.01.1996 N 149-КВ.
4. Расчет среднего заработка работника независимо от режима его работы производится исходя из фактически начисленной ему заработной платы и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя заработная плата. При этом календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале – по 28-е (29-е) число включительно).
Средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется за последние 12 календарных месяцев.
5. При исчислении среднего заработка из расчетного периода исключается время, а также начисленные за это время суммы, если:
а) за работником сохранялся средний заработок в соответствии с законодательством Российской Федерации, за исключением перерывов для кормления ребенка, предусмотренных трудовым законодательством Российской Федерации;
б) работник получал пособие по временной нетрудоспособности или пособие по беременности и родам;
в) работник не работал в связи с простоем по вине работодателя или по причинам, не зависящим от работодателя и работника;
г) работник не участвовал в забастовке, но в связи с этой забастовкой не имел возможности выполнять свою работу;
д) работнику предоставлялись дополнительные оплачиваемые выходные дни для ухода за детьми-инвалидами и инвалидами с детства;
е) работник в других случаях освобождался от работы с полным или частичным сохранением заработной платы или без оплаты в соответствии с законодательством Российской Федерации.
6. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период или за период, превышающий расчетный период, либо этот период состоял из времени, исключаемого из расчетного периода в соответствии с пунктом 5 настоящего Положения, средний заработок определяется исходя из суммы заработной платы, фактически начисленной за предшествующий период, равный расчетному.
7. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период и до начала расчетного периода, средний заработок определяется исходя из размера заработной платы, фактически начисленной за фактически отработанные работником дни в месяце наступления случая, с которым связано сохранение среднего заработка.
8. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период, до начала расчетного периода и до наступления случая, с которым связано сохранение среднего заработка, средний заработок определяется исходя из установленной ему тарифной ставки, оклада (должностного оклада).
9. При определении среднего заработка используется средний дневной заработок в следующих случаях:
для оплаты отпусков и выплаты компенсации за неиспользованные отпуска;
для других случаев, предусмотренных Трудовым кодексом Российской Федерации, кроме случая определения среднего заработка работников, которым установлен суммированный учет рабочего времени.
Средний заработок работника определяется путем умножения среднего дневного заработка на количество дней (календарных, рабочих) в периоде, подлежащем оплате.
Средний дневной заработок, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсаций за неиспользованные отпуска, исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные дни в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество фактически отработанных в этот период дней.
10. Средний дневной заработок для оплаты отпусков, предоставляемых в календарных днях, и выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы заработной платы, фактически начисленной за расчетный период, на 12 и на среднемесячное число календарных дней (29,3).
(в ред. Постановления Правительства РФ от 10.07.2014 N 642)
В случае если один или несколько месяцев расчетного периода отработаны не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, средний дневной заработок исчисляется путем деления суммы фактически начисленной заработной платы за расчетный период на сумму среднемесячного числа календарных дней (29,3), умноженного на количество полных календарных месяцев, и количества календарных дней в неполных календарных месяцах.
(в ред. Постановления Правительства РФ от 10.07.2014 N 642)
Количество календарных дней в неполном календарном месяце рассчитывается путем деления среднемесячного числа календарных дней (29,3) на количество календарных дней этого месяца и умножения на количество календарных дней, приходящихся на время, отработанное в данном месяце.
(в ред. Постановления Правительства РФ от 10.07.2014 N 642)
11. Средний дневной заработок для оплаты отпусков, предоставляемых в рабочих днях, а также для выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы фактически начисленной заработной платы на количество рабочих дней по календарю 6-дневной рабочей недели.
12. При работе на условиях неполного рабочего времени (неполной рабочей недели, неполного рабочего дня) средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется в соответствии с пунктами 10 и 11 настоящего Положения.
13. При определении среднего заработка работника, которому установлен суммированный учет рабочего времени, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсации за неиспользованные отпуска, используется средний часовой заработок.
Средний часовой заработок исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные часы в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество часов, фактически отработанных в этот период.
Средний заработок определяется путем умножения среднего часового заработка на количество рабочих часов по графику работника в периоде, подлежащем оплате.
14. При определении среднего заработка для оплаты дополнительных учебных отпусков оплате подлежат все календарные дни (включая нерабочие праздничные дни), приходящиеся на период таких отпусков, предоставляемых в соответствии со справкой-вызовом учебного заведения.
15. При определении среднего заработка премии и вознаграждения учитываются в следующем порядке:
ежемесячные премии и вознаграждения – фактически начисленные в расчетном периоде, но не более одной выплаты за каждый показатель за каждый месяц расчетного периода;
премии и вознаграждения за период работы, превышающий один месяц, – фактически начисленные в расчетном периоде за каждый показатель, если продолжительность периода, за который они начислены, не превышает продолжительности расчетного периода, и в размере месячной части за каждый месяц расчетного периода, если продолжительность периода, за который они начислены, превышает продолжительность расчетного периода;
вознаграждение по итогам работы за год, единовременное вознаграждение за выслугу лет (стаж работы), иные вознаграждения по итогам работы за год, начисленные за предшествующий событию календарный год, – независимо от времени начисления вознаграждения.
В случае если время, приходящееся на расчетный период, отработано не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, премии и вознаграждения учитываются при определении среднего заработка пропорционально времени, отработанному в расчетном периоде, за исключением премий, начисленных за фактически отработанное время в расчетном периоде (ежемесячные, ежеквартальные и др.).
Если работник проработал неполный рабочий период, за который начисляются премии и вознаграждения, и они были начислены пропорционально отработанному времени, они учитываются при определении среднего заработка исходя из фактически начисленных сумм в порядке, установленном настоящим пунктом.
16. При повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения средний заработок работников повышается в следующем порядке:
если повышение произошло в расчетный период, – выплаты, учитываемые при определении среднего заработка и начисленные в расчетном периоде за предшествующий повышению период времени, повышаются на коэффициенты, которые рассчитываются путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных в месяце последнего повышения тарифных ставок, окладов (должностных окладов), денежного вознаграждения, на тарифные ставки, оклады (должностные оклады), денежное вознаграждение, установленные в каждом из месяцев расчетного периода;
(в ред. Постановления Правительства РФ от 11.11.2009 N 916)
Постановления Правительства РФ от 11.11.2009 N 916)
если повышение произошло после расчетного периода до наступления случая, с которым связано сохранение среднего заработка, – повышается средний заработок, исчисленный за расчетный период;
если повышение произошло в период сохранения среднего заработка, – часть среднего заработка повышается с даты повышения тарифной ставки, оклада (должностного оклада), денежного вознаграждения до окончания указанного периода.
В случае если при повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения изменяются перечень ежемесячных выплат к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению и (или) их размеры, средний заработок повышается на коэффициенты, которые рассчитываются путем деления вновь установленных тарифных ставок, окладов (должностных окладов), денежного вознаграждения и ежемесячных выплат на ранее установленные тарифные ставки, оклады (должностные оклады), денежное вознаграждение и ежемесячные выплаты.
(абзац введен Постановлением Правительства РФ от 11.11.2009 N 916)
При повышении среднего заработка учитываются тарифные ставки, оклады (должностные оклады), денежное вознаграждение и выплаты, установленные к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в фиксированном размере (проценты, кратность), за исключением выплат, установленных к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в диапазоне значений (проценты, кратность).
При повышении среднего заработка выплаты, учитываемые при определении среднего заработка, установленные в абсолютных размерах, не повышаются.
17. Средний заработок, определенный для оплаты времени вынужденного прогула, подлежит повышению на коэффициент, рассчитанный путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных работнику с даты фактического начала работы после его восстановления на прежней работе, на тарифную ставку, оклад (должностной оклад), денежное вознаграждение, установленные в расчетном периоде, если за время вынужденного прогула в организации (филиале, структурном подразделении) повышались тарифные ставки, оклады (должностные оклады), денежное вознаграждение.
При этом в отношении выплат, установленных в фиксированном размере и в абсолютном размере, действует порядок, установленный пунктом 16 настоящего Положения.
18. Во всех случаях средний месячный заработок работника, отработавшего полностью в расчетный период норму рабочего времени и выполнившего нормы труда (трудовые обязанности), не может быть менее установленного федеральным законом минимального размера оплаты труда.
19. Лицам, работающим на условиях совместительства, средний заработок определяется в порядке, установленном настоящим Положением.
20. Для исчисления среднемесячной заработной платы руководителей, заместителей руководителей, главных бухгалтеров государственных внебюджетных фондов Российской Федерации, территориальных фондов обязательного медицинского страхования, государственных и муниципальных учреждений, государственных и муниципальных унитарных предприятий (далее – фонды, учреждения, предприятия), формируемой за счет всех источников финансового обеспечения и рассчитываемой за календарный год, и среднемесячной заработной платы работников фондов, учреждений, предприятий (без учета заработной платы руководителя, заместителей руководителя, главного бухгалтера) в целях определения предельного уровня их соотношения:
среднемесячная заработная плата работников фондов, учреждений, предприятий (без учета заработной платы руководителя, заместителей руководителя, главного бухгалтера) определяется путем деления суммы фактически начисленной заработной платы (включая выплаты, предусмотренные пунктом 2 настоящего Положения) таких работников списочного состава (без учета руководителя, заместителей руководителя, главного бухгалтера) на среднесписочную численность таких работников (без учета руководителя, заместителей руководителя, главного бухгалтера) за соответствующий календарный год и деления на 12 (количество месяцев в году). Определение среднесписочной численности указанных работников за соответствующий календарный год осуществляется в соответствии с методикой, используемой для целей федерального статистического наблюдения;
Определение среднесписочной численности указанных работников за соответствующий календарный год осуществляется в соответствии с методикой, используемой для целей федерального статистического наблюдения;
среднемесячная заработная плата руководителя, заместителя руководителя, главного бухгалтера фонда, учреждения, предприятия определяется путем деления суммы фактически начисленной заработной платы (включая выплаты, предусмотренные пунктом 2 настоящего Положения) соответствующему руководителю, заместителю руководителя, главному бухгалтеру за календарный год на 12 (количество месяцев в году). Если руководитель, заместитель руководителя, главный бухгалтер фонда, учреждения, предприятия состоял в трудовых отношениях с фондом, учреждением, предприятием неполный календарный год, то среднемесячная заработная плата определяется исходя из фактически отработанных соответствующим руководителем, заместителем руководителя, главным бухгалтером полных календарных месяцев.
Расчет среднемесячной заработной платы руководителя, заместителей руководителя, главного бухгалтера фонда, учреждения, предприятия осуществляется отдельно по должностям руководителя, главного бухгалтера и по каждой должности заместителя руководителя.
В фактической начисленной заработной плате для определения среднемесячной заработной платы, рассчитываемой в соответствии с абзацами первым – третьим настоящего пункта, не учитываются выплаты, предусмотренные пунктом 3 настоящего Положения, компенсации, выплачиваемые при прекращении трудового договора, в том числе за неиспользованный отпуск.
В случаях выполнения руководителем, заместителями руководителя, главным бухгалтером работы по совмещению должностей (профессий) или исполнения обязанностей временно отсутствующего работника без освобождения от основной работы в фактически начисленной заработной плате учитываются суммы, начисленные как по основной должности (профессии), так и по совмещаемой должности (профессии), а также начисленные за исполнение обязанностей временно отсутствующего работника без освобождения от основной работы. При работе по совместительству в фактически начисленной заработной плате учитываются только суммы фактически начисленной заработной платы по должности руководителя, заместителя руководителя, главного бухгалтера.
(п. 20 введен Постановлением Правительства РФ от 10.12.2016 N 1339)
(скачать)
Компенсация за ЕГЭ: Часто задаваемые вопросы
Вопрос 1:
Засчитывается ли в педагогический стаж время, в течение которого педагогический работник будет исполнять государственную обязанность – участие в проведении единого государственного экзамена?
Ответ:
Время, в течение которого педагогический работник будет исполнять государственную обязанность – участие в проведении единого государственного экзамена, не засчитывается в педагогический стаж, поскольку работник в указанный период педагогическую деятельность не осуществляет.
Вопрос 2:
Каким образом исполнение государственной обязанности – участие в проведении единого государственного экзамена отразится на отпускных педагогического работника образовательной организации?
Ответ:
В соответствии со статьей 139 Трудового кодекса Российской Федерации,Положением об особенностях порядка исчисления средней заработной платы, утвержденным Постановлением Правительства Российской Федерации от 24 декабря 2007 № 922:
расчет среднего заработка работника для исчисления ему отпускных независимо от режима его работы производится исходя из фактически начисленной ему заработной платы и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя заработная плата;
для расчета отпускных и выплаты компенсации за неиспользованные отпуска используется средний дневной заработок работника;
средний дневной заработок для оплаты отпусков, предоставляемых в календарных днях, и выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы заработной платы, фактически начисленной за расчетный период, на 12 и на среднемесячное число календарных дней (29,3).
Компенсация за участие в проведении единого государственного экзамена, выплачиваемая государственным казенным учреждением Новосибирской области «Новосибирский институт мониторинга и развития образования», в среднюю заработную плату по основному месту работы не включается.
Влияние участия педагогического работника в проведении единого государственного экзамена на размер его отпускных индивидуально и будет зависеть от продолжительности его отсутствия на рабочем месте. Вместе с тем, размер компенсации также индивидуален и зависит от продолжительности исполнения государственных обязанностей.
Вопрос 3:
Какое буквенное обозначение должны проставить в табеле учета использования рабочего времени педагогического работника по месту его основной работы при исполнении государственной обязанности – участии в проведении единого государственного экзамена?
Ответ:
В табеле учета использования рабочего времени педагогического работника по месту его основной работы при исполнении государственной обязанности – участие в проведении единого государственного экзамена проставляется код «Г» (исполнение государственных обязанностей).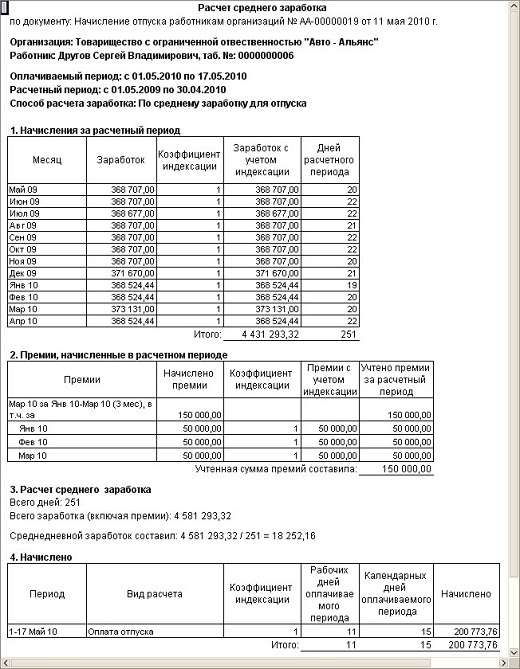
Вопрос 4:
Будет ли выплачиваться компенсация за работу по подготовке и проведению единого государственного экзамена директорам образовательных организаций и их заместителям?
Ответ:
В соответствии с частью 9 статьи 47 Федерального закона от 29.12.2012№ 273-ФЗ «Об образовании в Российской Федерации» компенсация за работу по подготовке и проведению единого государственного экзамена выплачивается педагогическим работникам.
Согласно номенклатуре должностей педагогических работников организаций, осуществляющих образовательную деятельность, должностей руководителей образовательных организаций, утвержденной постановлением Правительства Российской Федерации от 08.08.2013 № 678, директора образовательных организаций и их заместители к категории «педагогические работники» не относятся.
Вопрос 5:
Сколько составляет среднее время проверки работы одного обучающегося.
Ответ:
Среднее время проверки работы одного обучающегося составляет 9 минут.
Вопрос 6:
В каком порядке будет оплачена компенсация за работу по подготовке и проведению единого государственного экзамена педагогическому работнику.
Ответ:
Размер и порядок выплаты компенсации за работы по подготовке и проведению единого государственного экзамена педагогическим работникам, участвующим в проведении единого государственного экзамена, установлен постановлением Правительства Новосибирской области от 11.05.2017 № 181-п.
об исчислении средней заработной платы
ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПОСТАНОВЛЕНИЕ
от 24 декабря 2007 г. N 922
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
В соответствии со статьей 139 Трудового кодекса Российской Федерации Правительство Российской Федерации постановляет:
1.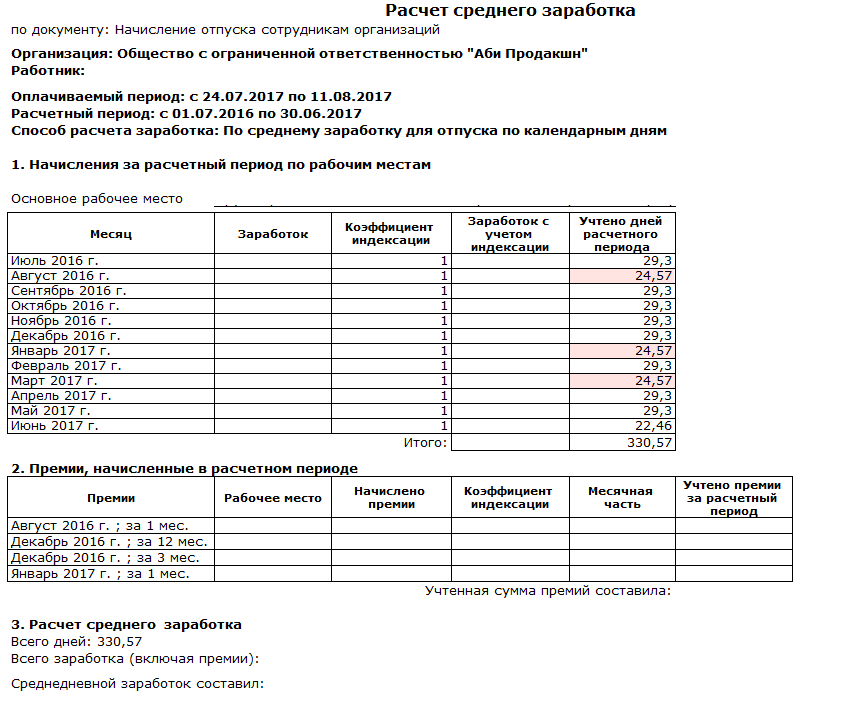 Утвердить прилагаемое Положение об особенностях порядка исчисления средней заработной платы.
Утвердить прилагаемое Положение об особенностях порядка исчисления средней заработной платы.
2. Министерству здравоохранения и социального развития Российской Федерации давать разъяснения по вопросам, связанным с применением Положения, утвержденного настоящим Постановлением.
3. Признать утратившим силу Постановление Правительства Российской Федерации от 11 апреля 2003 г. N 213 “Об особенностях порядка исчисления средней заработной платы” (Собрание законодательства Российской Федерации, 2003, N 16, ст. 1529).
Председатель Правительства
Российской Федерации
В.ЗУБКОВ
Утверждено
Постановлением Правительства
Российской Федерации
от 24 декабря 2007 г. N 922
ПОЛОЖЕНИЕ
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
1.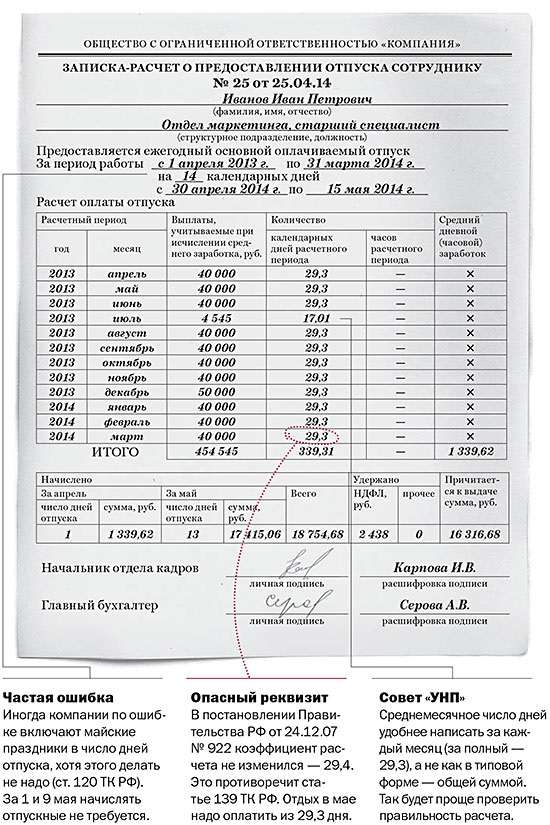 Настоящее Положение устанавливает особенности порядка исчисления средней заработной платы (среднего заработка) для всех случаев определения ее размера, предусмотренных Трудовым кодексом Российской Федерации (далее – средний заработок).
Настоящее Положение устанавливает особенности порядка исчисления средней заработной платы (среднего заработка) для всех случаев определения ее размера, предусмотренных Трудовым кодексом Российской Федерации (далее – средний заработок).
2. Для расчета среднего заработка учитываются все предусмотренные системой оплаты труда виды выплат, применяемые у соответствующего работодателя, независимо от источников этих выплат. К таким выплатам относятся:
а) заработная плата, начисленная работнику по тарифным ставкам, окладам (должностным окладам) за отработанное время;
б) заработная плата, начисленная работнику за выполненную работу по сдельным расценкам;
в) заработная плата, начисленная работнику за выполненную работу в процентах от выручки от реализации продукции (выполнения работ, оказания услуг), или комиссионное вознаграждение;
г) заработная плата, выданная в неденежной форме;
д) денежное вознаграждение (денежное содержание), начисленное за отработанное время лицам, замещающим государственные должности Российской Федерации, государственные должности субъектов Российской Федерации, депутатам, членам выборных органов местного самоуправления, выборным должностным лицам местного самоуправления, членам избирательных комиссий, действующих на постоянной основе;
е) денежное содержание, начисленное муниципальным служащим за отработанное время;
ж) начисленные в редакциях средств массовой информации и организациях искусства гонорар работников, состоящих в списочном составе этих редакций и организаций, и (или) оплата их труда, осуществляемая по ставкам (расценкам) авторского (постановочного) вознаграждения;
з) заработная плата, начисленная преподавателям учреждений начального и среднего профессионального образования за часы преподавательской работы сверх установленной и (или) уменьшенной годовой учебной нагрузки за текущий учебный год, независимо от времени начисления;
и) заработная плата, окончательно рассчитанная по завершении предшествующего событию календарного года, обусловленная системой оплаты труда, независимо от времени начисления;
к) надбавки и доплаты к тарифным ставкам, окладам (должностным окладам) за профессиональное мастерство, классность, выслугу лет (стаж работы), ученую степень, ученое звание, знание иностранного языка, работу со сведениями, составляющими государственную тайну, совмещение профессий (должностей), расширение зон обслуживания, увеличение объема выполняемых работ, руководство бригадой и другие;
л) выплаты, связанные с условиями труда, в том числе выплаты, обусловленные районным регулированием оплаты труда (в виде коэффициентов и процентных надбавок к заработной плате), повышенная оплата труда на тяжелых работах, работах с вредными и (или) опасными и иными особыми условиями труда, за работу в ночное время, оплата работы в выходные и нерабочие праздничные дни, оплата сверхурочной работы;
м) вознаграждение за выполнение функций классного руководителя педагогическим работникам государственных и муниципальных образовательных учреждений;
н) премии и вознаграждения, предусмотренные системой оплаты труда;
о) другие виды выплат по заработной плате, применяемые у соответствующего работодателя.
3. Для расчета среднего заработка не учитываются выплаты социального характера и иные выплаты, не относящиеся к оплате труда (материальная помощь, оплата стоимости питания, проезда, обучения, коммунальных услуг, отдыха и другие).
4. Расчет среднего заработка работника независимо от режима его работы производится исходя из фактически начисленной ему заработной платы и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя заработная плата. При этом календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале – по 28-е (29-е) число включительно).
Средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется за последние 12 календарных месяцев.
5. При исчислении среднего заработка из расчетного периода исключается время, а также начисленные за это время суммы, если:
а) за работником сохранялся средний заработок в соответствии с законодательством Российской Федерации, за исключением перерывов для кормления ребенка, предусмотренных трудовым законодательством Российской Федерации;
б) работник получал пособие по временной нетрудоспособности или пособие по беременности и родам;
в) работник не работал в связи с простоем по вине работодателя или по причинам, не зависящим от работодателя и работника;
г) работник не участвовал в забастовке, но в связи с этой забастовкой не имел возможности выполнять свою работу;
д) работнику предоставлялись дополнительные оплачиваемые выходные дни для ухода за детьми-инвалидами и инвалидами с детства;
е) работник в других случаях освобождался от работы с полным или частичным сохранением заработной платы или без оплаты в соответствии с законодательством Российской Федерации.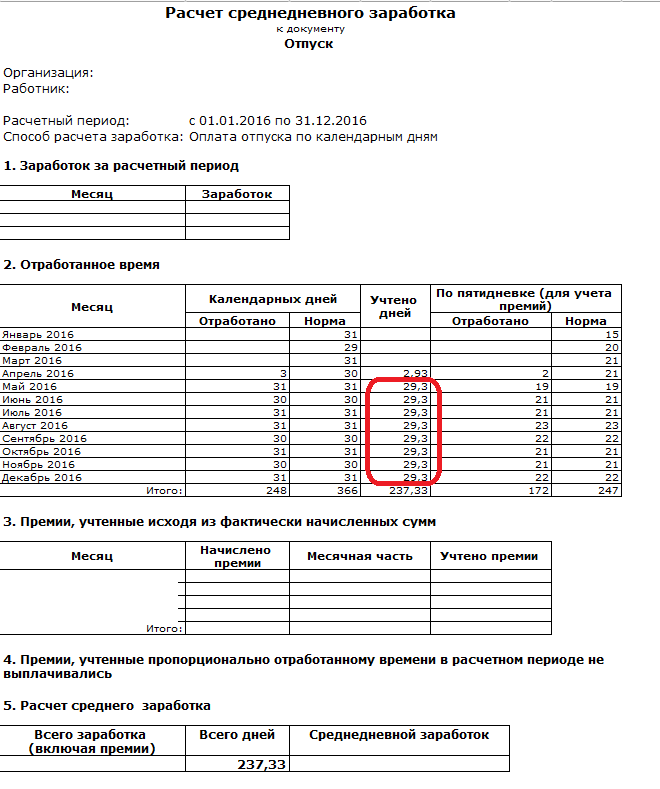
6. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период или за период, превышающий расчетный период, либо этот период состоял из времени, исключаемого из расчетного периода в соответствии с пунктом 5 настоящего Положения, средний заработок определяется исходя из суммы заработной платы, фактически начисленной за предшествующий период, равный расчетному.
7. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период и до начала расчетного периода, средний заработок определяется исходя из размера заработной платы, фактически начисленной за фактически отработанные работником дни в месяце наступления случая, с которым связано сохранение среднего заработка.
8. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период, до начала расчетного периода и до наступления случая, с которым связано сохранение среднего заработка, средний заработок определяется исходя из установленной ему тарифной ставки, оклада (должностного оклада).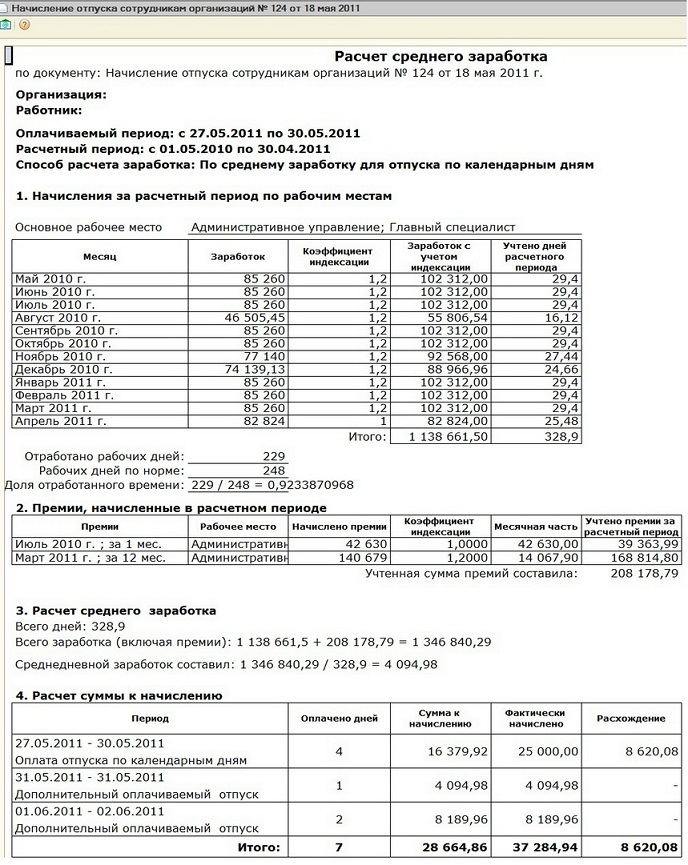
9. При определении среднего заработка используется средний дневной заработок в следующих случаях:
для оплаты отпусков и выплаты компенсации за неиспользованные отпуска;
для других случаев, предусмотренных Трудовым кодексом Российской Федерации, кроме случая определения среднего заработка работников, которым установлен суммированный учет рабочего времени.
Средний заработок работника определяется путем умножения среднего дневного заработка на количество дней (календарных, рабочих) в периоде, подлежащем оплате.
Средний дневной заработок, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсаций за неиспользованные отпуска, исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные дни в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество фактически отработанных в этот период дней.
10. Средний дневной заработок для оплаты отпусков, предоставляемых в календарных днях, и выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы заработной платы, фактически начисленной за расчетный период, на 12 и на среднемесячное число календарных дней (29,4).
Средний дневной заработок для оплаты отпусков, предоставляемых в календарных днях, и выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы заработной платы, фактически начисленной за расчетный период, на 12 и на среднемесячное число календарных дней (29,4).
В случае если один или несколько месяцев расчетного периода отработаны не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, средний дневной заработок исчисляется путем деления суммы фактически начисленной заработной платы за расчетный период на сумму среднемесячного числа календарных дней (29,4), умноженного на количество полных календарных месяцев, и количества календарных дней в неполных календарных месяцах.
Количество календарных дней в неполном календарном месяце рассчитывается путем деления среднемесячного числа календарных дней (29,4) на количество календарных дней этого месяца и умножения на количество календарных дней, приходящихся на время, отработанное в данном месяце.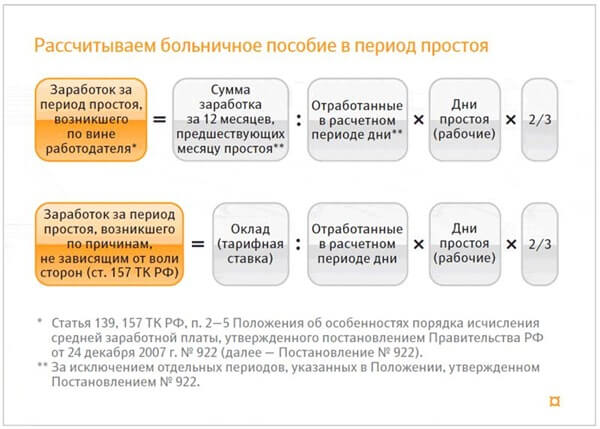
11. Средний дневной заработок для оплаты отпусков, предоставляемых в рабочих днях, а также для выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы фактически начисленной заработной платы на количество рабочих дней по календарю 6-дневной рабочей недели.
12. При работе на условиях неполного рабочего времени (неполной рабочей недели, неполного рабочего дня) средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется в соответствии с пунктами 10 и 11 настоящего Положения.
13. При определении среднего заработка работника, которому установлен суммированный учет рабочего времени, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсации за неиспользованные отпуска, используется средний часовой заработок.
Средний часовой заработок исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные часы в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество часов, фактически отработанных в этот период.
Средний заработок определяется путем умножения среднего часового заработка на количество рабочих часов по графику работника в периоде, подлежащем оплате.
14. При определении среднего заработка для оплаты дополнительных учебных отпусков оплате подлежат все календарные дни (включая нерабочие праздничные дни), приходящиеся на период таких отпусков, предоставляемых в соответствии со справкой-вызовом учебного заведения.
15. При определении среднего заработка премии и вознаграждения учитываются в следующем порядке:
ежемесячные премии и вознаграждения – фактически начисленные в расчетном периоде, но не более одной выплаты за каждый показатель за каждый месяц расчетного периода;
премии и вознаграждения за период работы, превышающий один месяц, – фактически начисленные в расчетном периоде за каждый показатель, если продолжительность периода, за который они начислены, не превышает продолжительности расчетного периода, и в размере месячной части за каждый месяц расчетного периода, если продолжительность периода, за который они начислены, превышает продолжительность расчетного периода;
вознаграждение по итогам работы за год, единовременное вознаграждение за выслугу лет (стаж работы), иные вознаграждения по итогам работы за год, начисленные за предшествующий событию календарный год, – независимо от времени начисления вознаграждения.
В случае если время, приходящееся на расчетный период, отработано не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, премии и вознаграждения учитываются при определении среднего заработка пропорционально времени, отработанному в расчетном периоде, за исключением премий, начисленных за фактически отработанное время в расчетном периоде (ежемесячные, ежеквартальные и др.).
Если работник проработал неполный рабочий период, за который начисляются премии и вознаграждения, и они были начислены пропорционально отработанному времени, они учитываются при определении среднего заработка исходя из фактически начисленных сумм в порядке, установленном настоящим пунктом.
16. При повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения средний заработок работников повышается в следующем порядке:
если повышение произошло в расчетный период, – выплаты, учитываемые при определении среднего заработка и начисленные в расчетном периоде за предшествующий повышению период времени, повышаются на коэффициенты, которые рассчитываются путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных в месяце наступления случая, с которым связано сохранение среднего заработка, на тарифные ставки, оклады (должностные оклады), денежное вознаграждение, установленные в каждом из месяцев расчетного периода;
если повышение произошло после расчетного периода до наступления случая, с которым связано сохранение среднего заработка, – повышается средний заработок, исчисленный за расчетный период;
если повышение произошло в период сохранения среднего заработка, – часть среднего заработка повышается с даты повышения тарифной ставки, оклада (должностного оклада), денежного вознаграждения до окончания указанного периода.
При повышении среднего заработка учитываются тарифные ставки, оклады (должностные оклады), денежное вознаграждение и выплаты, установленные к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в фиксированном размере (проценты, кратность), за исключением выплат, установленных к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в диапазоне значений (проценты, кратность).
При повышении среднего заработка выплаты, учитываемые при определении среднего заработка, установленные в абсолютных размерах, не повышаются.
17. Средний заработок, определенный для оплаты времени вынужденного прогула, подлежит повышению на коэффициент, рассчитанный путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных работнику с даты фактического начала работы после его восстановления на прежней работе, на тарифную ставку, оклад (должностной оклад), денежное вознаграждение, установленные в расчетном периоде, если за время вынужденного прогула в организации (филиале, структурном подразделении) повышались тарифные ставки, оклады (должностные оклады), денежное вознаграждение.
При этом в отношении выплат, установленных в фиксированном размере и в абсолютном размере, действует порядок, установленный пунктом 16 настоящего Положения.
18. Во всех случаях средний месячный заработок работника, отработавшего полностью в расчетный период норму рабочего времени и выполнившего нормы труда (трудовые обязанности), не может быть менее установленного федеральным законом минимального размера оплаты труда.
19. Лицам, работающим на условиях совместительства, средний заработок определяется в порядке, установленном настоящим Положением.
ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПОСТАНОВЛЕНИЕ
от 11 ноября 2009 г. N 916
О ВНЕСЕНИИ ИЗМЕНЕНИЙ
В ПУНКТ 16 ПОЛОЖЕНИЯ ОБ ОСОБЕННОСТЯХ ПОРЯДКА
ИСЧИСЛЕНИЯ СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
Правительство Российской Федерации постановляет:
Внести в пункт 16 Положения об особенностях порядка исчисления средней заработной платы, утвержденного Постановлением Правительства Российской Федерации от 24 декабря 2007 г. N 922 (Собрание законодательства Российской Федерации, 2007, N 53, ст. 6618), следующие изменения:
N 922 (Собрание законодательства Российской Федерации, 2007, N 53, ст. 6618), следующие изменения:
а) в абзаце втором слова “наступления случая, с которым связано сохранение среднего заработка” заменить словами “последнего повышения тарифных ставок, окладов (должностных окладов), денежного вознаграждения”;
б) дополнить после абзаца четвертого абзацем следующего содержания:
“В случае если при повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения изменяются перечень ежемесячных выплат к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению и (или) их размеры, средний заработок повышается на коэффициенты, которые рассчитываются путем деления вновь установленных тарифных ставок, окладов (должностных окладов), денежного вознаграждения и ежемесячных выплат на ранее установленные тарифные ставки, оклады (должностные оклады), денежное вознаграждение и ежемесячные выплаты. “.
“.
Председатель Правительства
Российской Федерации
В.ПУТИН
Постановление Правительства РФ от 24.12.2007 N 922 (ред. от 10.12.2016) “Об особенностях порядка исчисления средней заработной платы” – последняя редакция
ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПОСТАНОВЛЕНИЕ
от 24 декабря 2007 г. N 922
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
В соответствии со статьей 139 Трудового кодекса Российской Федерации Правительство Российской Федерации постановляет:
1. Утвердить прилагаемое Положение об особенностях порядка исчисления средней заработной платы.
2. Министерству труда и социальной защиты Российской Федерации давать разъяснения по вопросам, связанным с применением Положения, утвержденного настоящим Постановлением.
3. Признать утратившим силу Постановление Правительства Российской Федерации от 11 апреля 2003 г. N 213 “Об особенностях порядка исчисления средней заработной платы” (Собрание законодательства Российской Федерации, 2003, N 16, ст. 1529).
1529).
Председатель Правительства
Российской Федерации
В.ЗУБКОВ
Утверждено
Постановлением Правительства
Российской Федерации
от 24 декабря 2007 г. N 922
ПОЛОЖЕНИЕ
ОБ ОСОБЕННОСТЯХ ПОРЯДКА ИСЧИСЛЕНИЯ
СРЕДНЕЙ ЗАРАБОТНОЙ ПЛАТЫ
1. Настоящее Положение устанавливает особенности порядка исчисления средней заработной платы (среднего заработка) для всех случаев определения ее размера, предусмотренных Трудовым кодексом Российской Федерации (далее – средний заработок).
2. Для расчета среднего заработка учитываются все предусмотренные системой оплаты труда виды выплат, применяемые у соответствующего работодателя, независимо от источников этих выплат. К таким выплатам относятся:
а) заработная плата, начисленная работнику по тарифным ставкам, окладам (должностным окладам) за отработанное время;
б) заработная плата, начисленная работнику за выполненную работу по сдельным расценкам;
в) заработная плата, начисленная работнику за выполненную работу в процентах от выручки от реализации продукции (выполнения работ, оказания услуг), или комиссионное вознаграждение;
г) заработная плата, выданная в неденежной форме;
д) денежное вознаграждение (денежное содержание), начисленное за отработанное время лицам, замещающим государственные должности Российской Федерации, государственные должности субъектов Российской Федерации, депутатам, членам выборных органов местного самоуправления, выборным должностным лицам местного самоуправления, членам избирательных комиссий, действующих на постоянной основе;
е) денежное содержание, начисленное муниципальным служащим за отработанное время;
ж) начисленные в редакциях средств массовой информации и организациях искусства гонорар работников, состоящих в списочном составе этих редакций и организаций, и (или) оплата их труда, осуществляемая по ставкам (расценкам) авторского (постановочного) вознаграждения;
з) заработная плата, начисленная преподавателям профессиональных образовательных организаций за часы преподавательской работы сверх установленной и (или) уменьшенной годовой учебной нагрузки за текущий учебный год, независимо от времени начисления;
и) заработная плата, окончательно рассчитанная по завершении предшествующего событию календарного года, обусловленная системой оплаты труда, независимо от времени начисления;
к) надбавки и доплаты к тарифным ставкам, окладам (должностным окладам) за профессиональное мастерство, классность, выслугу лет (стаж работы), знание иностранного языка, работу со сведениями, составляющими государственную тайну, совмещение профессий (должностей), расширение зон обслуживания, увеличение объема выполняемых работ, руководство бригадой и другие;
л) выплаты, связанные с условиями труда, в том числе выплаты, обусловленные районным регулированием оплаты труда (в виде коэффициентов и процентных надбавок к заработной плате), повышенная оплата труда на тяжелых работах, работах с вредными и (или) опасными и иными особыми условиями труда, за работу в ночное время, оплата работы в выходные и нерабочие праздничные дни, оплата сверхурочной работы;
м) вознаграждение за выполнение функций классного руководителя педагогическим работникам государственных и муниципальных образовательных организаций;
н) премии и вознаграждения, предусмотренные системой оплаты труда;
о) другие виды выплат по заработной плате, применяемые у соответствующего работодателя.
3. Для расчета среднего заработка не учитываются выплаты социального характера и иные выплаты, не относящиеся к оплате труда (материальная помощь, оплата стоимости питания, проезда, обучения, коммунальных услуг, отдыха и другие).
4. Расчет среднего заработка работника независимо от режима его работы производится исходя из фактически начисленной ему заработной платы и фактически отработанного им времени за 12 календарных месяцев, предшествующих периоду, в течение которого за работником сохраняется средняя заработная плата. При этом календарным месяцем считается период с 1-го по 30-е (31-е) число соответствующего месяца включительно (в феврале – по 28-е (29-е) число включительно).
Средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется за последние 12 календарных месяцев.
5. При исчислении среднего заработка из расчетного периода исключается время, а также начисленные за это время суммы, если:
а) за работником сохранялся средний заработок в соответствии с законодательством Российской Федерации, за исключением перерывов для кормления ребенка, предусмотренных трудовым законодательством Российской Федерации;
б) работник получал пособие по временной нетрудоспособности или пособие по беременности и родам;
в) работник не работал в связи с простоем по вине работодателя или по причинам, не зависящим от работодателя и работника;
г) работник не участвовал в забастовке, но в связи с этой забастовкой не имел возможности выполнять свою работу;
д) работнику предоставлялись дополнительные оплачиваемые выходные дни для ухода за детьми-инвалидами и инвалидами с детства;
е) работник в других случаях освобождался от работы с полным или частичным сохранением заработной платы или без оплаты в соответствии с законодательством Российской Федерации.
6. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период или за период, превышающий расчетный период, либо этот период состоял из времени, исключаемого из расчетного периода в соответствии с пунктом 5 настоящего Положения, средний заработок определяется исходя из суммы заработной платы, фактически начисленной за предшествующий период, равный расчетному.
7. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период и до начала расчетного периода, средний заработок определяется исходя из размера заработной платы, фактически начисленной за фактически отработанные работником дни в месяце наступления случая, с которым связано сохранение среднего заработка.
8. В случае если работник не имел фактически начисленной заработной платы или фактически отработанных дней за расчетный период, до начала расчетного периода и до наступления случая, с которым связано сохранение среднего заработка, средний заработок определяется исходя из установленной ему тарифной ставки, оклада (должностного оклада).
9. При определении среднего заработка используется средний дневной заработок в следующих случаях:
для оплаты отпусков и выплаты компенсации за неиспользованные отпуска;
для других случаев, предусмотренных Трудовым кодексом Российской Федерации, кроме случая определения среднего заработка работников, которым установлен суммированный учет рабочего времени.
Средний заработок работника определяется путем умножения среднего дневного заработка на количество дней (календарных, рабочих) в периоде, подлежащем оплате.
Средний дневной заработок, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсаций за неиспользованные отпуска, исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные дни в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество фактически отработанных в этот период дней.
10. Средний дневной заработок для оплаты отпусков, предоставляемых в календарных днях, и выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы заработной платы, фактически начисленной за расчетный период, на 12 и на среднемесячное число календарных дней (29,3).
В случае если один или несколько месяцев расчетного периода отработаны не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, средний дневной заработок исчисляется путем деления суммы фактически начисленной заработной платы за расчетный период на сумму среднемесячного числа календарных дней (29,3), умноженного на количество полных календарных месяцев, и количества календарных дней в неполных календарных месяцах.
Количество календарных дней в неполном календарном месяце рассчитывается путем деления среднемесячного числа календарных дней (29,3) на количество календарных дней этого месяца и умножения на количество календарных дней, приходящихся на время, отработанное в данном месяце.
11. Средний дневной заработок для оплаты отпусков, предоставляемых в рабочих днях, а также для выплаты компенсации за неиспользованные отпуска исчисляется путем деления суммы фактически начисленной заработной платы на количество рабочих дней по календарю 6-дневной рабочей недели.
12. При работе на условиях неполного рабочего времени (неполной рабочей недели, неполного рабочего дня) средний дневной заработок для оплаты отпусков и выплаты компенсации за неиспользованные отпуска исчисляется в соответствии с пунктами 10 и 11 настоящего Положения.
13. При определении среднего заработка работника, которому установлен суммированный учет рабочего времени, кроме случаев определения среднего заработка для оплаты отпусков и выплаты компенсации за неиспользованные отпуска, используется средний часовой заработок.
Средний часовой заработок исчисляется путем деления суммы заработной платы, фактически начисленной за отработанные часы в расчетном периоде, включая премии и вознаграждения, учитываемые в соответствии с пунктом 15 настоящего Положения, на количество часов, фактически отработанных в этот период.
Средний заработок определяется путем умножения среднего часового заработка на количество рабочих часов по графику работника в периоде, подлежащем оплате.
14. При определении среднего заработка для оплаты дополнительных учебных отпусков оплате подлежат все календарные дни (включая нерабочие праздничные дни), приходящиеся на период таких отпусков, предоставляемых в соответствии со справкой-вызовом учебного заведения.
15. При определении среднего заработка премии и вознаграждения учитываются в следующем порядке:
ежемесячные премии и вознаграждения – фактически начисленные в расчетном периоде, но не более одной выплаты за каждый показатель за каждый месяц расчетного периода;
премии и вознаграждения за период работы, превышающий один месяц, – фактически начисленные в расчетном периоде за каждый показатель, если продолжительность периода, за который они начислены, не превышает продолжительности расчетного периода, и в размере месячной части за каждый месяц расчетного периода, если продолжительность периода, за который они начислены, превышает продолжительность расчетного периода;
вознаграждение по итогам работы за год, единовременное вознаграждение за выслугу лет (стаж работы), иные вознаграждения по итогам работы за год, начисленные за предшествующий событию календарный год, – независимо от времени начисления вознаграждения.
В случае если время, приходящееся на расчетный период, отработано не полностью или из него исключалось время в соответствии с пунктом 5 настоящего Положения, премии и вознаграждения учитываются при определении среднего заработка пропорционально времени, отработанному в расчетном периоде, за исключением премий, начисленных за фактически отработанное время в расчетном периоде (ежемесячные, ежеквартальные и др.).
Если работник проработал неполный рабочий период, за который начисляются премии и вознаграждения, и они были начислены пропорционально отработанному времени, они учитываются при определении среднего заработка исходя из фактически начисленных сумм в порядке, установленном настоящим пунктом.
16. При повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения средний заработок работников повышается в следующем порядке:
если повышение произошло в расчетный период, – выплаты, учитываемые при определении среднего заработка и начисленные в расчетном периоде за предшествующий повышению период времени, повышаются на коэффициенты, которые рассчитываются путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных в месяце последнего повышения тарифных ставок, окладов (должностных окладов), денежного вознаграждения, на тарифные ставки, оклады (должностные оклады), денежное вознаграждение, установленные в каждом из месяцев расчетного периода;
если повышение произошло после расчетного периода до наступления случая, с которым связано сохранение среднего заработка, – повышается средний заработок, исчисленный за расчетный период;
если повышение произошло в период сохранения среднего заработка, – часть среднего заработка повышается с даты повышения тарифной ставки, оклада (должностного оклада), денежного вознаграждения до окончания указанного периода.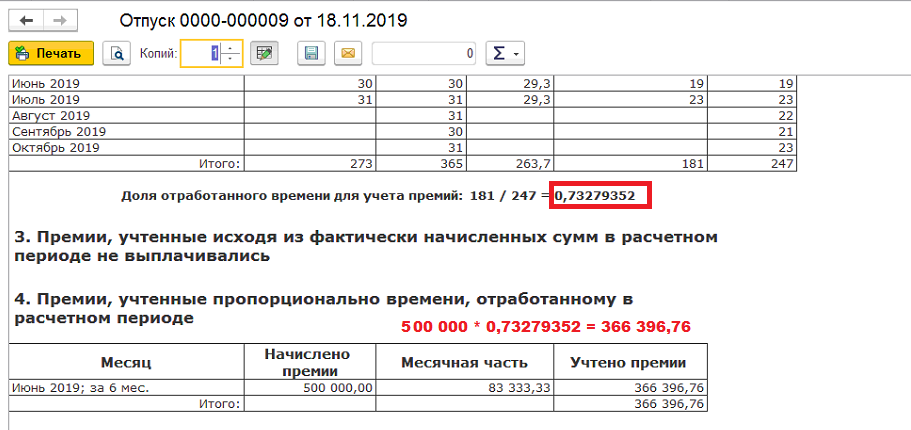
В случае если при повышении в организации (филиале, структурном подразделении) тарифных ставок, окладов (должностных окладов), денежного вознаграждения изменяются перечень ежемесячных выплат к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению и (или) их размеры, средний заработок повышается на коэффициенты, которые рассчитываются путем деления вновь установленных тарифных ставок, окладов (должностных окладов), денежного вознаграждения и ежемесячных выплат на ранее установленные тарифные ставки, оклады (должностные оклады), денежное вознаграждение и ежемесячные выплаты.
При повышении среднего заработка учитываются тарифные ставки, оклады (должностные оклады), денежное вознаграждение и выплаты, установленные к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в фиксированном размере (проценты, кратность), за исключением выплат, установленных к тарифным ставкам, окладам (должностным окладам), денежному вознаграждению в диапазоне значений (проценты, кратность).
При повышении среднего заработка выплаты, учитываемые при определении среднего заработка, установленные в абсолютных размерах, не повышаются.
17. Средний заработок, определенный для оплаты времени вынужденного прогула, подлежит повышению на коэффициент, рассчитанный путем деления тарифной ставки, оклада (должностного оклада), денежного вознаграждения, установленных работнику с даты фактического начала работы после его восстановления на прежней работе, на тарифную ставку, оклад (должностной оклад), денежное вознаграждение, установленные в расчетном периоде, если за время вынужденного прогула в организации (филиале, структурном подразделении) повышались тарифные ставки, оклады (должностные оклады), денежное вознаграждение.
При этом в отношении выплат, установленных в фиксированном размере и в абсолютном размере, действует порядок, установленный пунктом 16 настоящего Положения.
18. Во всех случаях средний месячный заработок работника, отработавшего полностью в расчетный период норму рабочего времени и выполнившего нормы труда (трудовые обязанности), не может быть менее установленного федеральным законом минимального размера оплаты труда.
19. Лицам, работающим на условиях совместительства, средний заработок определяется в порядке, установленном настоящим Положением.
20. Для исчисления среднемесячной заработной платы руководителей, заместителей руководителей, главных бухгалтеров государственных внебюджетных фондов Российской Федерации, территориальных фондов обязательного медицинского страхования, государственных и муниципальных учреждений, государственных и муниципальных унитарных предприятий (далее – фонды, учреждения, предприятия), формируемой за счет всех источников финансового обеспечения и рассчитываемой за календарный год, и среднемесячной заработной платы работников фондов, учреждений, предприятий (без учета заработной платы руководителя, заместителей руководителя, главного бухгалтера) в целях определения предельного уровня их соотношения:
среднемесячная заработная плата работников фондов, учреждений, предприятий (без учета заработной платы руководителя, заместителей руководителя, главного бухгалтера) определяется путем деления суммы фактически начисленной заработной платы (включая выплаты, предусмотренные пунктом 2 настоящего Положения) таких работников списочного состава (без учета руководителя, заместителей руководителя, главного бухгалтера) на среднесписочную численность таких работников (без учета руководителя, заместителей руководителя, главного бухгалтера) за соответствующий календарный год и деления на 12 (количество месяцев в году). Определение среднесписочной численности указанных работников за соответствующий календарный год осуществляется в соответствии с методикой, используемой для целей федерального статистического наблюдения;
Определение среднесписочной численности указанных работников за соответствующий календарный год осуществляется в соответствии с методикой, используемой для целей федерального статистического наблюдения;
среднемесячная заработная плата руководителя, заместителя руководителя, главного бухгалтера фонда, учреждения, предприятия определяется путем деления суммы фактически начисленной заработной платы (включая выплаты, предусмотренные пунктом 2 настоящего Положения) соответствующему руководителю, заместителю руководителя, главному бухгалтеру за календарный год на 12 (количество месяцев в году). Если руководитель, заместитель руководителя, главный бухгалтер фонда, учреждения, предприятия состоял в трудовых отношениях с фондом, учреждением, предприятием неполный календарный год, то среднемесячная заработная плата определяется исходя из фактически отработанных соответствующим руководителем, заместителем руководителя, главным бухгалтером полных календарных месяцев.
Расчет среднемесячной заработной платы руководителя, заместителей руководителя, главного бухгалтера фонда, учреждения, предприятия осуществляется отдельно по должностям руководителя, главного бухгалтера и по каждой должности заместителя руководителя.
В фактической начисленной заработной плате для определения среднемесячной заработной платы, рассчитываемой в соответствии с абзацами первым – третьим настоящего пункта, не учитываются выплаты, предусмотренные пунктом 3 настоящего Положения, компенсации, выплачиваемые при прекращении трудового договора, в том числе за неиспользованный отпуск.
В случаях выполнения руководителем, заместителями руководителя, главным бухгалтером работы по совмещению должностей (профессий) или исполнения обязанностей временно отсутствующего работника без освобождения от основной работы в фактически начисленной заработной плате учитываются суммы, начисленные как по основной должности (профессии), так и по совмещаемой должности (профессии), а также начисленные за исполнение обязанностей временно отсутствующего работника без освобождения от основной работы. При работе по совместительству в фактически начисленной заработной плате учитываются только суммы фактически начисленной заработной платы по должности руководителя, заместителя руководителя, главного бухгалтера.
Влияние анизотропии излучения на флуоресцентную спектроскопию и измерения расстояний FRET
Влияние ЭА на измерения интенсивности
Рассеяние флуоресцентного света частично сохраняет поляризацию излучаемого света, параллельную поляризации возбуждающего света, если ориентация диполя не теряется полностью из-за вращения диффузия в течение времени жизни возбуждения. Компоненты интенсивности флуоресценции с поляризацией, параллельной и перпендикулярной поляризации возбуждения, называются параллельной ( I ‖ ) и перпендикулярной ( I ⊥ ) компонентами интенсивности (раздел 5.1.1.1 Валера (17)). Отношение перпендикулярных/параллельных компонент интенсивности зависит только от ЭА образца: I ⊥ / I ‖ = (1 − r )/(1 + 2 r ). Для изотропных образцов любая измеренная интенсивность флуоресценции I представляет собой линейную комбинацию параллельной и перпендикулярной составляющих интенсивности с коэффициентами, зависящими только от конфигурации флуорометра, а не от свойств образца: ‖ + (1 – P ) I ⊥ I ⊥ ) W ,
(1)
, где W , вес, зависит от интенсивности освещения и монохроматора и эффективности детектора, а также фракцию параллельного освещения, p , зависит только от конфигурации флюорометра и может быть рассчитано как средний квадрат квадрата угла между поляризациями освещения и детектирования по профилям интенсивности освещения и детектора. Сигнал флюорометра, усредняющий по всей сфере, имеет значение p = 2 / 3 . Значения p , отличные от 1 / 3 , приводят к расхождению измеренной интенсивности с осредненной по всей сфере интенсивностью 〈 I 〉: )/〈 I 〉 = (3 p − 1) r .
Сигнал флюорометра, усредняющий по всей сфере, имеет значение p = 2 / 3 . Значения p , отличные от 1 / 3 , приводят к расхождению измеренной интенсивности с осредненной по всей сфере интенсивностью 〈 I 〉: )/〈 I 〉 = (3 p − 1) r .
(2)
Мы рассчитали значения p для флюорометра с цилиндрически симметричными профилями освещения и светосбора.В оставшейся части этого раздела мы используем рассчитанные значения коэффициента p , чтобы найти EA по измерениям интенсивности.
Профили освещенности и чувствительности детектора рассматриваем как тонкие конические оболочки. Если коэффициент p представляет собой билинейную сумму слагаемых, линейных по параметрам источника света, и слагаемых, линейных по параметрам детектора, с коэффициентами, зависящими от угла между источником света и детектором, то коэффициенты источника и детектора можно усреднить независимо друг от друга по произвольным цилиндрически симметричным профилям. Геометрия флюорометра описана в . Оптические оси системы освещения и детектора расположены в горизонтальной плоскости и пересекаются в середине камеры с образцом под углом ϕ . Предполагается, что флуориметр скорректирован на бесконечность с параллельными лучами перед коллиматором возбуждения и после коллиматора излучения. Флуорометр оснащен линейными поляризаторами возбуждения и излучения, расположенными в параллельных пучках. Предположим сначала, что монохроматоры источника света и детектора не имеют поляризационного смещения, т.е.т. е. вес w одинаков для всех ориентаций поляризатора. Монохроматоры со смещением поляризации будут рассмотрены позже. EA будет рассчитываться по четырем измерениям интенсивности: I HH , I HV , I VH и I VV , с горизонтальной или вертикальной ориентацией (s) или исходного (первый индекс) и детекторного (второй индекс) поляризаторов.
Геометрия флюорометра описана в . Оптические оси системы освещения и детектора расположены в горизонтальной плоскости и пересекаются в середине камеры с образцом под углом ϕ . Предполагается, что флуориметр скорректирован на бесконечность с параллельными лучами перед коллиматором возбуждения и после коллиматора излучения. Флуорометр оснащен линейными поляризаторами возбуждения и излучения, расположенными в параллельных пучках. Предположим сначала, что монохроматоры источника света и детектора не имеют поляризационного смещения, т.е.т. е. вес w одинаков для всех ориентаций поляризатора. Монохроматоры со смещением поляризации будут рассмотрены позже. EA будет рассчитываться по четырем измерениям интенсивности: I HH , I HV , I VH и I VV , с горизонтальной или вертикальной ориентацией (s) или исходного (первый индекс) и детекторного (второй индекс) поляризаторов.
Геометрия флуорометра. Параллельный пучок света от источника, расположенного на оси z , распространяется через линейный поляризатор и цилиндрически-симметричную коллиматорную оптику на малый образец, расположенный в начале системы координат.Сигнал флуоресценции от образца собирается цилиндрически-симметричной коллимирующей оптикой в параллельный пучок, который проходит через линейный поляризатор в детектор. Детектор расположен в горизонтальной плоскости xz под углом ϕ с осью z . Цилиндрически-симметричная коллиматорная оптика источника и приемника света может быть охарактеризована b – и d -факторами соответственно.
Параллельный пучок света от источника, расположенного на оси z , распространяется через линейный поляризатор и цилиндрически-симметричную коллиматорную оптику на малый образец, расположенный в начале системы координат.Сигнал флуоресценции от образца собирается цилиндрически-симметричной коллимирующей оптикой в параллельный пучок, который проходит через линейный поляризатор в детектор. Детектор расположен в горизонтальной плоскости xz под углом ϕ с осью z . Цилиндрически-симметричная коллиматорная оптика источника и приемника света может быть охарактеризована b – и d -факторами соответственно.
Доля параллельного освещения для компонентов интенсивности рассчитывается с использованием программного обеспечения Mathematica (Wolfram Research, Champaign, IL) в зависимости от углов поляризатора источника (S) и детектора (D), ψ S и ψ D , соответственно, считается из горизонтальной плоскости (ψ = 0):
P (ψ S , ψ d ) = ⅙ [2 + D S D D + 3 B S B D (COS (2ψ S ) COS (2ψ D ) + Cosφsin (2ψ S ) SIN (2ψ D )) + ( P 2 (COS Φ) – 1) ( D S + B S COS (2ψ S )) ( D D + B D COS (2ψ D ))],
(3)
, где коэффициенты d = 〈 P 2 (cos α )〉 и b = 〈5 9006 056 (α/2)〉 усредняются по соответствующим профилям освещения (индекс S) или светосбора (индекс D) с весами, пропорциональными нормализованной интенсивности света, α — угол конуса между направлением луча в камере с образцом и ось, P 2 ( x ) ≡ ½(3 x 2 − 1) — второй полином Лежандра. Коэффициенты b – и d равны 1 для коллиматоров с малой числовой апертурой (ЧА), что может вызывать поляризацию измеряемого сигнала ( p ≠ ⅓). Более высокие значения NA приводят к меньшим значениям b – и d -факторов, что вызывает деполяризацию ( p ≅ ⅓). Значения коэффициентов d – и b для типичных оптических конфигураций рассчитаны ниже. Доли параллельного освещения для четырех ортогональных ориентаций поляризатора составляют p HH = p (0, 0), pHV=p(0,π2), pVH=p(π2,0) и pVV=p( π2, π2).Если для измерения интенсивности не используется поляризатор, p=〈p(ψS,ψD)〉ψS,ψD=13+16P2(cosϕ)dSdD, а погрешность измерения интенсивности составляет
Коэффициенты b – и d равны 1 для коллиматоров с малой числовой апертурой (ЧА), что может вызывать поляризацию измеряемого сигнала ( p ≠ ⅓). Более высокие значения NA приводят к меньшим значениям b – и d -факторов, что вызывает деполяризацию ( p ≅ ⅓). Значения коэффициентов d – и b для типичных оптических конфигураций рассчитаны ниже. Доли параллельного освещения для четырех ортогональных ориентаций поляризатора составляют p HH = p (0, 0), pHV=p(0,π2), pVH=p(π2,0) и pVV=p( π2, π2).Если для измерения интенсивности не используется поляризатор, p=〈p(ψS,ψD)〉ψS,ψD=13+16P2(cosϕ)dSdD, а погрешность измерения интенсивности составляет
δ = ½ r P 2 (cos ϕ) d S d D .
(4)
Мы заметили, что этот результат может быть получен непосредственно из теоремы Солейе (17–19), если d -факторов рассматривать как «коэффициенты деполяризации» для источника света и детектора.
EA флуоресцентного образца можно рассчитать по четырем измерениям интенсивности по уравнению. 3 как
R≡i‖-i⊥i‖ + 2i⊥ = A1-A12-4 (ℑ2-1) A22A2,
(5)
где
ℑ 2 ≡ ( I VV I HH ) / ( I VH I HV ),
(6)
A 1 = (3 P VV – 1 ) + (3 P HH – 1) – ℑ 2 2 [(3 P VH – 1) + (3 P HV – 1)],
(7 )
A 2 = ℑ 2 (3 P VH – 1) (3 P HV – 1) – (3 P VV – 1) (3 p HH − 1).
(8)
Для лазерного гелевого сканера или микроскопа с ϕ = 0° или 180° достаточно только двух измерений интенсивности (поскольку I VV = I HH и 8 = I HV ) и уравнение 5 можно упростить как
R = 2 / [3 B S B D ( ℑ + 1) / ( ℑ – 1) – D S d D ],
(9)
где ℑ = I VV / I HV .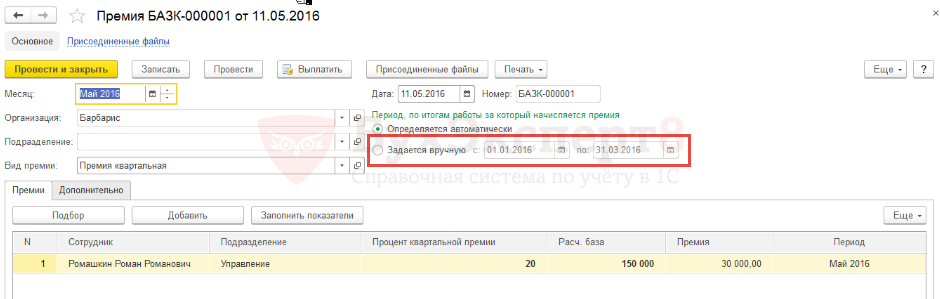 Уравнение 9 полезно, и EA можно измерить, если только b S b D = 0,
Уравнение 9 полезно, и EA можно измерить, если только b S b D = 0,
Теперь мы принимаем во внимание, что эффективность дифракционных решеток, используемых в флуорометрических монохроматорах, может изменяться на порядок в зависимости от изменение длины волны и поляризации. Эффективность источника света или детектора монохроматоров (с вертикальными или горизонтальными прорельями) для вертикальных или горизонтальных поляризаций составляет е SV , E SH , E DV , E DH , соответственно; они являются функциями длины волны.Весовой коэффициент в уравнении. 1 зависит от эффективности и ориентации поляризаторов как
W (ψ S , ψ d ) = ( E SH COS 2 ψ S + E SV SIN 2 ψ S ) ( E DH COS 2 ψ D + E DV SIN 2 ψ D ).
(10)
Долю параллельной составляющей интенсивности для неполяризованного измерения можно вычислить аналитически с помощью компьютера для произвольных цилиндрически-симметричных профилей освещения и детектирования, но нам не удалось упростить громоздкий результат до краткой формы.В пределе малых числовых апертур осветительной и детекторной оптики коэффициенты b – и d приближаются к 1 снизу, а доля параллельного освещения составляет
p = ( g G + COS 2 Φ) / (1 + G + G + G G ),
(11)
Где факторы G ≡ E DV / E DH и G ≡ 9000 и G ≡ E SV / E SH могут быть рассчитаны из четырех поляризованных измерений интенсивности как
G = (12sin2φ + (12sin2φ) 2 + ℑ2Cos2φ) (IHV / IHHH ),
(12)
g=(12sin2ϕ+(12sin2ϕ)2+ℑ2cos2ϕ)(IVH/IHH).
(13)
Коэффициент g является функцией длины волны источника света, описывающей смещение поляризации источника света. Его определение простое, но мы не можем найти его в литературе, поэтому мы ввели его по аналогии с G -фактором, который является функцией длины волны излучения, описывающей смещение поляризации детектора. Если ϕ = 90 o , скобки в уравнениях 12 и 13 равны 1, а уравнение. 12 принимает общую форму G = I HV / I HH .
Пример: b- и d-факторы для типичных аппаратных конфигураций
Если параллельный линейно поляризованный лазерный луч перекрывает коллиматорную линзу источника света с одинаковой интенсивностью, его d – и b -факторы равны
dS=P2 ((1−x−2)ln(1−x2)),bS=54−x−2(1−1−x2)+14(1−x−2)ln(1−x2),
(14 )
, где x = NA/ n – отношение числовой апертуры объектива к показателю преломления среды. Если линза объектива имеет 100% эффективность светосбора для всех углов апертуры, ее коэффициенты d – и b равны ()
Если линза объектива имеет 100% эффективность светосбора для всех углов апертуры, ее коэффициенты d – и b равны ()
dD=(1−x2+1−x2)/2,bD=(2+ 1−x2−x2/4)/3.
(15)
EA изотропного образца можно измерить с помощью микроскопа с флуоресцентным освещением полного внутреннего отражения через призму с линейно поляризованным лазерным лучом. EA можно рассчитать с помощью уравнения. 9, если известны b – и d -факторы, поляризация освещения фиксируется, а линейным поляризатором в канале наблюдения изменяется только поляризация излучения. Существуют две поляризации лазерного луча, создающего затухающую волну: s-поляризованная с электрическим полем падающего света и затухающей волны, параллельная границе раздела двух сред, и р-поляризованная с электрическим полем в плоскости падающего света. и отраженные лучи.Отношение компонент поляризации, перпендикулярных и параллельных границе раздела сред, для р-поляризованной затухающей волны составляет и стекло, а θ — угол падения (уравнения 5 и 6 Аксельрода (20)).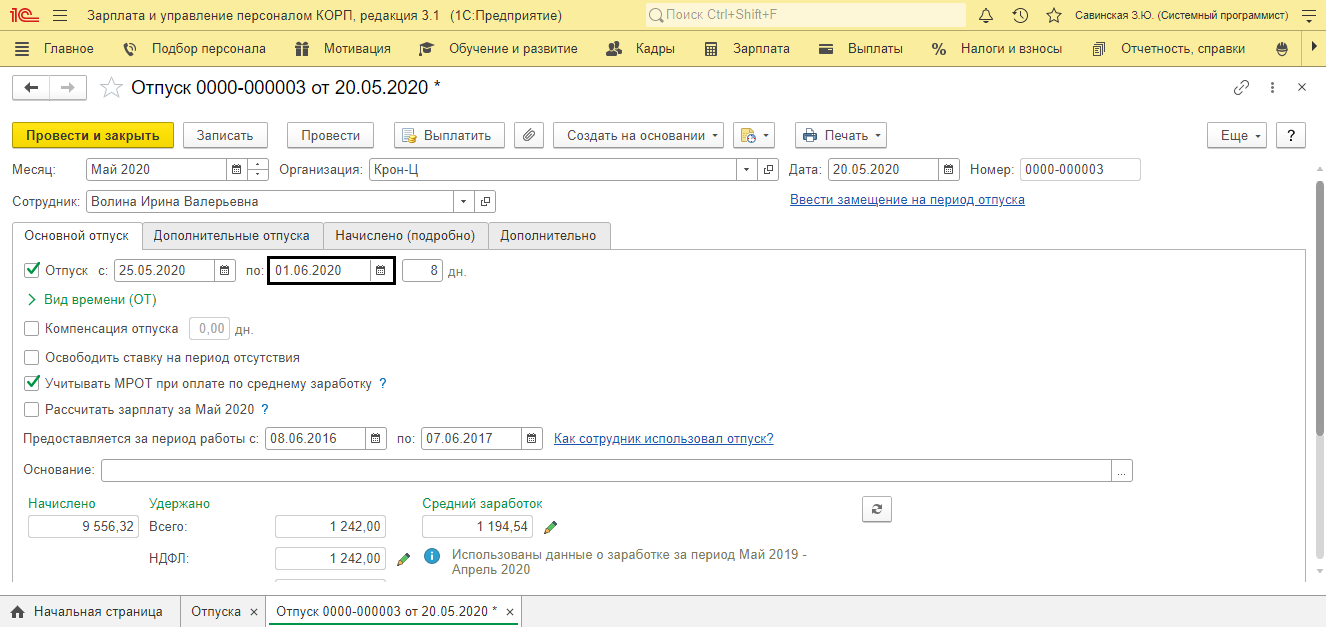 Для P-поляризации B – и D – и D – и D – и D S = 1 и B S = – N 2 / (2Sin 2 θ – n 2 ).Для s-поляризованного освещения деполяризация отсутствует, и d S = b S = 1. d – и b -факторы детектора рассчитаны выше для объектива микроскопа ( уравнение 15). Результаты могут быть обобщены для наблюдения одиночной молекулы.
Для P-поляризации B – и D – и D – и D – и D S = 1 и B S = – N 2 / (2Sin 2 θ – n 2 ).Для s-поляризованного освещения деполяризация отсутствует, и d S = b S = 1. d – и b -факторы детектора рассчитаны выше для объектива микроскопа ( уравнение 15). Результаты могут быть обобщены для наблюдения одиночной молекулы.
Коэффициенты b – и d в зависимости от NA/ n для лазерного освещения, переполняющего конденсорную линзу с одинаковой интенсивностью, и для объектива, собирающего флуоресцентный свет с одинаковой эффективностью для всех телесных углов в пределах его апертуры , рассчитанный с использованием уравнений.14 и 15.
Мы описываем гель-лазерный сканер Typhoon Trio компании GE Healthcare (Waukesha, WI) в качестве примера реального аппаратного оборудования. По данным технической поддержки компании, лазерные сканеры серии Typhoon используют два объектива с фокусным расстоянием 6 мм (настройка: валик) и 9 мм (настройка: +3 мм), оба с числовой апертурой = 0,7. Для освещения и детектирования используется один и тот же объектив, но диаметр луча освещения 0,7 мм намного меньше апертуры объектива, а апертура NA объектива применима только для детектирования.Влияние освещенности NA можно пренебрегать: N A S ≅ 0, B S = D S = 1. B – и D -продуктов для детектор можно рассчитать по уравнению 15: b D = 0,86, d D = 0,61. В лазерном сканере Typhoon в качестве детектора используются фиксированные фильтры и трубка фотоумножителя, и предполагается, что он не имеет смещения поляризации или длины волны. Используя уравнение4 мы вычисляем ошибку неполяризованной интенсивности как функцию EA образца: δ = 0,31 r .
По данным технической поддержки компании, лазерные сканеры серии Typhoon используют два объектива с фокусным расстоянием 6 мм (настройка: валик) и 9 мм (настройка: +3 мм), оба с числовой апертурой = 0,7. Для освещения и детектирования используется один и тот же объектив, но диаметр луча освещения 0,7 мм намного меньше апертуры объектива, а апертура NA объектива применима только для детектирования.Влияние освещенности NA можно пренебрегать: N A S ≅ 0, B S = D S = 1. B – и D -продуктов для детектор можно рассчитать по уравнению 15: b D = 0,86, d D = 0,61. В лазерном сканере Typhoon в качестве детектора используются фиксированные фильтры и трубка фотоумножителя, и предполагается, что он не имеет смещения поляризации или длины волны. Используя уравнение4 мы вычисляем ошибку неполяризованной интенсивности как функцию EA образца: δ = 0,31 r . Если EA образца неизвестен (-0,2 ≤ r ≤ 0,4), возможная ошибка интенсивности составляет от -6% до +12%.
Если EA образца неизвестен (-0,2 ≤ r ≤ 0,4), возможная ошибка интенсивности составляет от -6% до +12%.
Оценка FRET DOF из EA
Безызлучательный перенос энергии возбуждения между флуорофорами или от флуорофора к тушителю в классической электродинамике можно описать как ближнепольное диполь-дипольное взаимодействие. Здесь мы предполагаем, что донорный и акцепторный красители представляют собой два простых диполя.Более сложные случаи можно рассматривать как комбинацию нескольких диполей (21), но это выходит за рамки данной статьи. Мы описываем геометрию FRET-пары полярными углами для донора θ d и акцептора θ a , отсчитываемыми от оси, соединяющей донор и акцептор, и двугранным углом между плоскостями диполя, ϕ da (). Угол между донором и акцептором β DA может быть рассчитан как функция других углов
COSβ da = Cosθ A COSθ D + Sinθ A Sinθ D COSφ DE .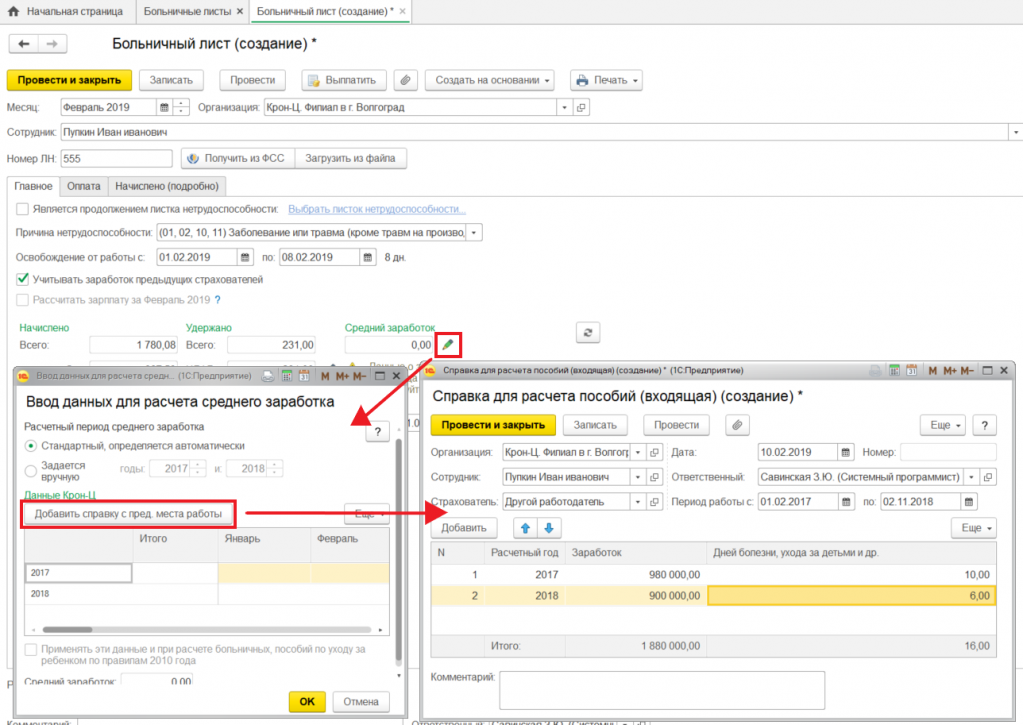 .
.
Из уравнения. 16, и из того факта, что −1 ≤ cosϕ da ≤ 1, легко вывести тривиальное, но важное геометрическое неравенство, отсутствующее в работе Dale et al. (7):
cos(θ d + θ a ) ≤ cosβ da ≤ ≤ cos(θ d − θ a ).
(17)
Если известно значение cosβ da , то можно использовать неравенство 17 как ограничение на допустимую площадь полярных углов.
Согласно теории Ферстера (глава 9 Лаковича (17)), скорость передачи энергии пропорциональна степени свободы, κ 2 = (3cosθ a cosθ d −cosβ da ) 2 .Радиус Фёрстера, R 0 , определяется как расстояние, на котором эффективность FRET составляет 50% для данного значения DOF; таким образом, он пропорционален κ26 (7,17). Расстояние между флуорофорами можно рассчитать по эффективности FRET, E и R 0 как R=R0E-1-16∝κ26. Среднее значение телесного угла степени свободы равно 2 / 3 . Ориентационное усреднение κ 2 справедливо только в том случае, если ориентации донорного и акцепторного диполей изотропно перераспределяются по всей сфере в течение времени жизни возбуждения донора (т.т. е. нет истощения населения для штатов с более высокими значениями степени свободы по сравнению с выжившими штатами с меньшей глубиной свободы). Расхождение в измерениях расстояний из-за значений ГРИП, отличных от усредненного значения по углу, можно описать поправочным коэффициентом Δ≡κ2/236, равным отношению истинного расстояния к кажущемуся расстоянию, рассчитанному для κ 2 = ⅔ . Ниже мы оцениваем диапазон поправочного коэффициента по измерениям ЭА.
Среднее значение телесного угла степени свободы равно 2 / 3 . Ориентационное усреднение κ 2 справедливо только в том случае, если ориентации донорного и акцепторного диполей изотропно перераспределяются по всей сфере в течение времени жизни возбуждения донора (т.т. е. нет истощения населения для штатов с более высокими значениями степени свободы по сравнению с выжившими штатами с меньшей глубиной свободы). Расхождение в измерениях расстояний из-за значений ГРИП, отличных от усредненного значения по углу, можно описать поправочным коэффициентом Δ≡κ2/236, равным отношению истинного расстояния к кажущемуся расстоянию, рассчитанному для κ 2 = ⅔ . Ниже мы оцениваем диапазон поправочного коэффициента по измерениям ЭА.
Будем считать, что донорный и акцепторный флуорофоры присоединены к большой и неподвижной (в течение времени возбуждения) макромолекуле; флуорофоры диффундируют только под углом по отношению ко всей макромолекуле, а расстояние между донором и акцептором фиксировано.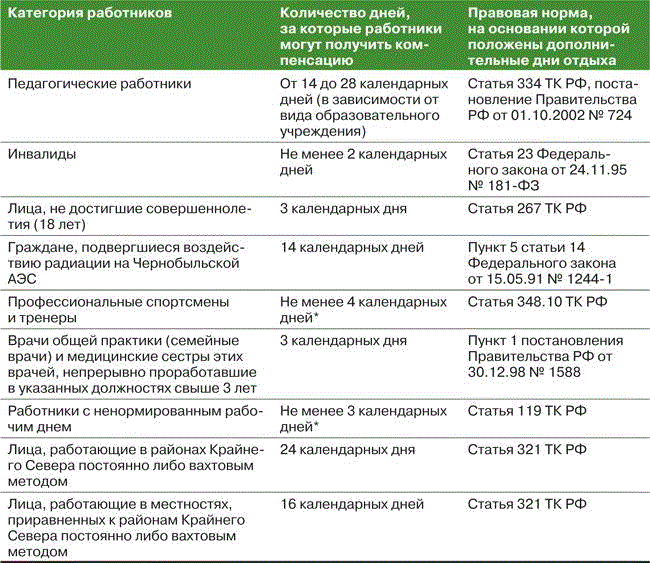 Согласно теореме Солейе, EA сигнала FRET является произведением предельной анизотропии ⅖, факторов донорной и акцепторной аксиальной деполяризации ddxd и daxd и фактора деполяризации P 2 (cosβ da ), что соответствует угол между центрами осей симметрии распределения доноров и акцепторов, β da (7):
Согласно теореме Солейе, EA сигнала FRET является произведением предельной анизотропии ⅖, факторов донорной и акцепторной аксиальной деполяризации ddxd и daxd и фактора деполяризации P 2 (cosβ da ), что соответствует угол между центрами осей симметрии распределения доноров и акцепторов, β da (7):
rFRET=25ddxddaxaP2(cosβda).
(18)
Мы можем рассчитать ddxd из EA, rd=25dd=25(ddxd)2, для донорного флуорофора, присоединенного к макромолекуле в отсутствие акцепторного флуорофора:
где d d фактор деполяризации только для донора, который равен квадрату фактора аксиальной деполяризации, ddxd.Фактор осевой деполяризации акцептора, daxa, можно рассчитать аналогичным образом. (Если акцептор не является флуорофором, а темновым гасителем, его коэффициент аксиальной деполяризации не может быть получен из измеренного EA. Эту проблему можно решить, если акцептор не является простым диполем и может быть почти изотропным по своей природе. ) Знак ddxd может быть отрицательным, если r d ≤ 0,1 для вращающейся связи или r d ≤ 1/160 для заполненных конусов угловых распределений донорного диполя относительно макромолекулы (7).Отрицательный знак факторов деполяризации может привести к двум или даже четырем различным возможностям для степени свободы, но нетрудно рассмотреть их все с помощью компьютера. Как правило, следует выбирать самый широкий диапазон для оценки погрешности.
) Знак ddxd может быть отрицательным, если r d ≤ 0,1 для вращающейся связи или r d ≤ 1/160 для заполненных конусов угловых распределений донорного диполя относительно макромолекулы (7).Отрицательный знак факторов деполяризации может привести к двум или даже четырем различным возможностям для степени свободы, но нетрудно рассмотреть их все с помощью компьютера. Как правило, следует выбирать самый широкий диапазон для оценки погрешности.
Мы можем рассчитать cosβ da из FRET-поляризации, используя уравнение. 18:
cosβda=13+53rFRETddxddaxa.
(20)
Знак cosβ da не определен, но можно считать cosβ da всегда положительным, а 0 o ≤ β da ≤ 90 dipoleo уравнениями связи, так как радиационные дипольные моменты (в отличие от ориентации флуоресцентных молекул) определяются не векторами, а проективными векторами, т.е.т. е. противоположные ориентации эквивалентны. По тем же соображениям мы можем ограничиться 0° ≤ θ d ≤ 90° и 0° ≤ θ a ≤ 90°, если это необходимо. Угол между донором и акцептором, β da , является единственным углом, который можно найти из измерений ЭА или любых других измерений поляризации изотропных образцов. Измерения других углов, влияющих на DOF, требуют некоторых дополнительных знаний о макромолекуле, ее точках прикрепления флуорофора и ее конформационной динамике, и такие знания трудно получить экспериментально (1).
По тем же соображениям мы можем ограничиться 0° ≤ θ d ≤ 90° и 0° ≤ θ a ≤ 90°, если это необходимо. Угол между донором и акцептором, β da , является единственным углом, который можно найти из измерений ЭА или любых других измерений поляризации изотропных образцов. Измерения других углов, влияющих на DOF, требуют некоторых дополнительных знаний о макромолекуле, ее точках прикрепления флуорофора и ее конформационной динамике, и такие знания трудно получить экспериментально (1).
Степень свободы, усредненная по цилиндрически симметричным распределениям акцептора и донора, была получена Dale et al. (7):
κ2=ddxddaxaκ02+(1−daxa)(ddxdcos2θd+13)+(1−ddxd)(daxacos2θa+13),
(21)
где
(22)
Степень свободы в уравнении. 21 зависит только от двух неизвестных углов, θ d и θ a , ограниченных ограничением 17; cosβ da можно найти из уравнения. 20. Минимумы и максимумы степени свободы из уравнения. 21 были рассчитаны неправильно в Dale et al. (7) независимо от использования ограничения 17 (это можно проверить численно). Возможный диапазон глубины резкости можно найти с помощью компьютера.
21 были рассчитаны неправильно в Dale et al. (7) независимо от использования ограничения 17 (это можно проверить численно). Возможный диапазон глубины резкости можно найти с помощью компьютера.
Если EA сигнала FRET неизвестен или если уравнение 18 не может быть решен для β da с хорошей точностью, минимальное и максимальное значения ГРИП с положительными факторами деполяризации (7) равны
κmin2=23(1−(52rd+52ra)/2),κmax2=23 (1+52р+52ра+352р52ра).
(23)
Если возможны отрицательные факторы деполяризации (см.19 и последующее обсуждение), минимальное и максимальное значения степени свободы можно найти с помощью компьютера, перепробовав все комбинации знаков в уравнении. 21 ().
Минимальное и максимальное значения степени свободы ( A ) и поправочного коэффициента расстояния ( B ) в зависимости от EA, если донор и акцептор имеют одинаковое значение EA: r d = р а = р . График рассчитывается с использованием уравнения. 23 для положительного ( сплошная линия ) и отрицательного ( пунктирная линия (возможно только для r ≤ 0.1)) факторы аксиальной деполяризации. Легко видеть, что диапазон для степени свободы медленно сходится к ⅔ при r d, a → 0. Типичный диапазон EA, 0,15–0,25, соответствует −15 + 20% или даже −20 + 25 %, погрешность измерения расстояния FRET.
График рассчитывается с использованием уравнения. 23 для положительного ( сплошная линия ) и отрицательного ( пунктирная линия (возможно только для r ≤ 0.1)) факторы аксиальной деполяризации. Легко видеть, что диапазон для степени свободы медленно сходится к ⅔ при r d, a → 0. Типичный диапазон EA, 0,15–0,25, соответствует −15 + 20% или даже −20 + 25 %, погрешность измерения расстояния FRET.
Пример: неопределенность степени свободы для комплекса интегразы ВИЧ-1
Комплекс интегразы ВИЧ-1 состоит из четырех молекул интегразы и двух двухцепочечных фрагментов ДНК (22). Фрагменты ДНК в комплексе могут быть двумя концами одной длинной молекулы ДНК, как в случае настоящей ДНК ВИЧ-1, или могут иметь форму двух более коротких фрагментов ДНК.Комплекс трудно очистить in vitro, но его можно отделить от непрореагировавшего субстрата с помощью нативного гель-электрофореза. Атомно-силовые микроскопические изображения комплексов не содержат информации с достаточно высоким разрешением, а также страдают от возможных деформаций комплексов во время поверхностной иммобилизации, необходимой для атомно-силовой микроскопии. В качестве примера мы используем измерение расстояния FRET на комплексе интегразы ВИЧ-1 с хвостами ДНК, помеченными красителями Cy3 и Cy5 вблизи концов.
В качестве примера мы используем измерение расстояния FRET на комплексе интегразы ВИЧ-1 с хвостами ДНК, помеченными красителями Cy3 и Cy5 вблизи концов.
Мы выделяем правильно собранный комплекс из непрореагировавшего субстрата с помощью электрофореза в нативном агарозном геле.Соответствующую полосу на геле идентифицировали и измеряли с помощью лазерного сканера геля с длинами волн возбуждения донора и акцептора в донорном, акцепторном и FRET-канале. Для флуорометрических измерений вырезали кусочки геля, содержащие интересующую полосу, и помещали в кювету с буфером или смесью глицерин-буфер. Нашей целью было оценить расстояния между различными точками ДНК внутри комплекса. Результаты по структуре комплекса ВИЧ-1 будут опубликованы в отдельной статье.Мы не обсуждаем здесь какие-либо конструктивные детали комплекса.
EA сигналов донора, акцептора и FRET были измерены для расчета неопределенности расстояния из-за DOF. Результаты измерений EA для двух конфигураций пар FRET суммированы в . Диапазон глубины резкости и неопределенность расстояния рассчитывались для двух пар позиций маркировки. Первые две строки таблицы соответствуют паре FRET в позиции маркировки 1-1′, представляя случаи неизвестного и известного EA сигнала FRET.Последняя строка соответствует положению 2-2′ пары FRET с более высокими значениями EA донора и акцептора и известной EA FRET. Если FRET EA известен, угол между донором и акцептором, β da , рассчитывали по уравнению. 20. Для положения 1-1′ с известным FRET EA допустимый диапазон полярных углов, θ d и θ a , из неравенства 17 вычерчен в ; поправочные коэффициенты ориентации диполя и расстояния, рассчитанные с использованием уравнений 20–22 представлены в зависимости от полярных углов в пределах их допустимой площади.Если FRET EA неизвестен, диапазоны глубины резкости и расстояния рассчитываются по уравнению. 23. Диапазоны глубины резкости и расстояния нанесены графически для случая r d = r a .
Диапазон глубины резкости и неопределенность расстояния рассчитывались для двух пар позиций маркировки. Первые две строки таблицы соответствуют паре FRET в позиции маркировки 1-1′, представляя случаи неизвестного и известного EA сигнала FRET.Последняя строка соответствует положению 2-2′ пары FRET с более высокими значениями EA донора и акцептора и известной EA FRET. Если FRET EA известен, угол между донором и акцептором, β da , рассчитывали по уравнению. 20. Для положения 1-1′ с известным FRET EA допустимый диапазон полярных углов, θ d и θ a , из неравенства 17 вычерчен в ; поправочные коэффициенты ориентации диполя и расстояния, рассчитанные с использованием уравнений 20–22 представлены в зависимости от полярных углов в пределах их допустимой площади.Если FRET EA неизвестен, диапазоны глубины резкости и расстояния рассчитываются по уравнению. 23. Диапазоны глубины резкости и расстояния нанесены графически для случая r d = r a .
Допустимая площадь на плоскости полярного угла (θ d , θ a ) ( черный прямоугольник ; симметричный θ d ↔ θ a ) имеет выполненное неравенство 17. Для расчета этой площади мы используем r d = 0,275, r a = 0.292 и r FRET = -0,026. Поскольку радиационные дипольные моменты являются проективными векторами, достаточно рассмотреть только четверть симметричной допустимой площади с 0≤θd≤π2 и 0≤θa≤π2.
Графики DOFS ( A ) и коэффициент коррекции расстояния, δ ( B ) для R D = 0,275, R A = 0,292 и R FRET = −0,026 в зависимости от θ a − θ d и θ a + θ d на допустимом участке от .Графики рассчитаны с использованием уравнений 20–22.
Таблица 1
DOF Диапазон и неуверенности расстояния
| позиция | R D R R A | R FRET | β DA | κ 2 Range | R неопределенность | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1-1 ‘ | 0. 275 275 | 0.292 | – | – | 0.11-3.21 | -26 + 30% | |||
| 1-1 | 0.275 | 0.292 | 0.292 | 58.6 ° | 0.15-2.50 | -22 + 25% | |||
| 2 ‘ | 0.340 | 0.316 | 0.230 | 0.230 | 0.230 | 25. 1 ° 1 ° | 0.11 9982 | 0.11-3.33 | -26 + 31% |
Уравнение 4 описывает систематическую ошибку в интенсивности флуоресценции, измеренной для лазерного гелевого сканера из-за советник выборки.В лазерном сканере могут отсутствовать поляризаторы, но ЭА можно измерить с помощью объемного флуорометра. Коррекция интенсивности для лазерного сканера Typhoon обсуждалась выше.
%PDF-1.6 % 1616 0 объект > эндообъект внешняя ссылка 1616 92 0000000016 00000 н 0000003462 00000 н 0000003572 00000 н 0000003704 00000 н 0000005032 00000 н 0000005141 00000 н 0000005257 00000 н 0000005371 00000 н 0000005483 00000 н 0000006124 00000 н 0000006245 00000 н 0000006798 00000 н 0000006909 00000 н 0000007465 00000 н 0000008112 00000 н 0000008719 00000 н 0000009309 00000 н 0000009882 00000 н 0000010438 00000 н 0000011424 00000 н 0000012212 00000 н 0000014945 00000 н 0000029879 00000 н 0000030554 00000 н 0000299825 00000 н 0000299991 00000 н 0000300169 00000 н 0000300342 00000 н 0000300527 00000 н 0000300705 00000 н 0000300893 00000 н 0000301093 00000 н 0000301279 00000 н 0000301450 00000 н 0000301660 00000 н 0000301839 00000 н 0000302035 00000 н 0000302239 00000 н 0000302412 00000 н 0000302593 00000 н 0000302855 00000 н 0000303052 00000 н 0000303222 00000 н 0000303399 00000 н 0000303572 00000 н 0000303762 00000 н 0000303932 00000 н 0000304109 00000 н 0000304355 00000 н 0000304521 00000 н 0000304692 00000 н 0000304869 00000 н 0000305040 00000 н 0000307625 00000 н 0000307844 00000 н 0000308720 00000 н 0000310713 00000 н 0000315175 00000 н 0000316326 00000 н 0000320762 00000 н 0000321645 00000 н 0000326064 00000 н 0000326793 00000 н 0000329071 00000 н 0000329761 00000 н 0000352400 00000 н 0000392912 00000 н 0000396172 00000 н 0000408420 00000 н 0000409912 00000 н 0000410569 00000 н 0000411226 00000 н 0000412027 00000 н 0000413268 00000 н 0000413992 00000 н 00005
00000 н 0000595056 00000 н 0000595873 00000 н 0000596876 00000 н 0000600913 00000 н 0000601637 00000 н 0000646265 00000 н 0000667762 00000 н 0000668672 00000 н 0000669545 00000 н 0000670175 00000 н 0000670812 00000 н 0000671449 00000 н 0000672082 00000 н 0000672726 00000 н 0000673357 00000 н 0000002136 00000 н трейлер ]>> startxref 0 %%EOF 1707 0 объект>поток xkLg~7YA %PDF-1.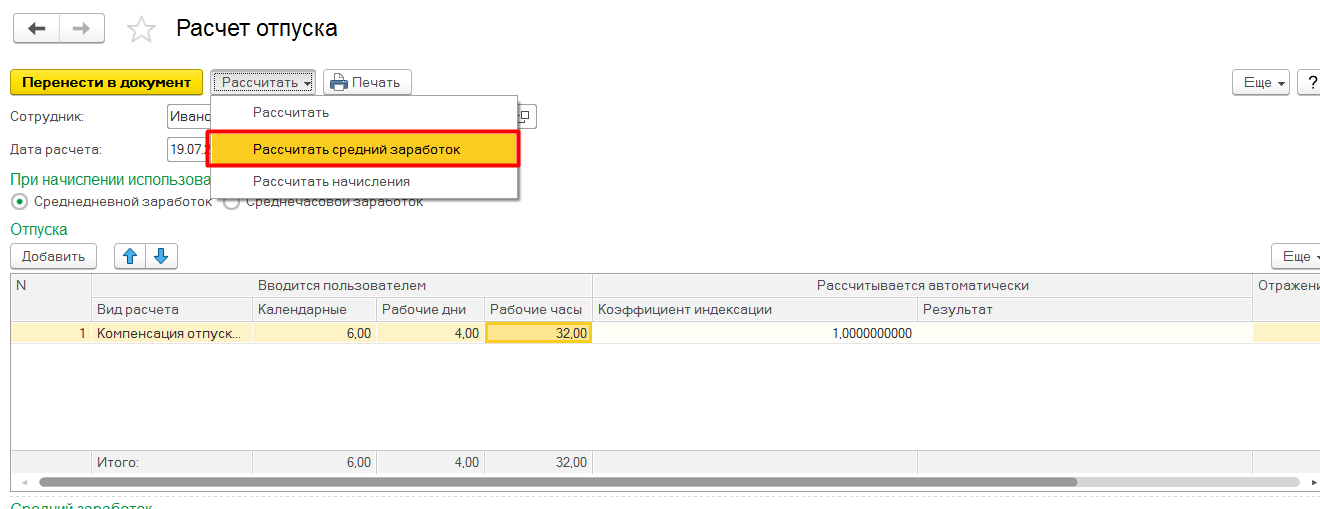 7
%
804 0 объект
>
эндообъект
внешняя ссылка
804 143
0000000016 00000 н
0000004567 00000 н
0000004729 00000 н
0000005080 00000 н
0000005599 00000 н
0000006435 00000 н
0000006485 00000 н
0000006539 00000 н
0000006740 00000 н
0000006923 00000 н
0000007856 00000 н
0000008818 00000 н
0000008999 00000 н
0000009515 00000 н
0000009707 00000 н
0000009865 00000 н
0000010229 00000 н
0000011079 00000 н
0000011270 00000 н
0000011464 00000 н
0000027887 00000 н
0000028841 00000 н
0000037268 00000 н
0000043135 00000 н
0000043193 00000 н
0000043300 00000 н
0000043388 00000 н
0000043521 00000 н
0000043672 00000 н
0000043810 00000 н
0000043943 00000 н
0000044083 00000 н
0000044230 00000 н
0000044378 00000 н
0000044523 00000 н
0000044632 00000 н
0000044738 00000 н
0000044840 00000 н
0000045008 00000 н
0000045103 00000 н
0000045200 00000 н
0000045305 00000 н
0000045405 00000 н
0000045506 00000 н
0000045621 00000 н
0000045721 00000 н
0000045825 00000 н
0000045972 00000 н
0000046125 00000 н
0000046246 00000 н
0000046404 00000 н
0000046554 00000 н
0000046699 00000 н
0000046796 00000 н
0000046904 00000 н
0000047064 00000 н
0000047161 00000 н
0000047269 00000 н
0000047429 00000 н
0000047582 00000 н
0000047702 00000 н
0000047899 00000 н
0000048010 00000 н
0000048119 00000 н
0000048268 00000 н
0000048379 00000 н
0000048487 00000 н
0000048613 00000 н
0000048733 00000 н
0000048830 00000 н
0000048998 00000 н
0000049106 00000 н
0000049228 00000 н
0000049335 00000 н
0000049444 00000 н
0000049595 00000 н
0000049744 00000 н
0000049852 00000 н
0000050010 00000 н
0000050158 00000 н
0000050300 00000 н
0000050419 00000 н
0000050535 00000 н
0000050674 00000 н
0000050824 00000 н
0000050919 00000 н
0000051073 00000 н
0000051184 00000 н
0000051360 00000 н
0000051529 00000 н
0000051625 00000 н
0000051806 00000 н
0000051901 00000 н
0000052051 00000 н
0000052159 00000 н
0000052267 00000 н
0000052375 00000 н
0000052489 00000 н
0000052586 00000 н
0000052735 00000 н
0000052879 00000 н
0000053034 00000 н
0000053132 00000 н
0000053241 00000 н
0000053358 00000 н
0000053473 00000 н
0000053636 00000 н
0000053785 00000 н
0000053921 00000 н
0000054082 00000 н
0000054231 00000 н
0000054421 00000 н
0000054578 00000 н
0000054695 00000 н
0000054836 00000 н
0000054944 00000 н
0000055177 00000 н
0000055290 00000 н
0000055402 00000 н
0000055524 00000 н
0000055637 00000 н
0000055749 00000 н
0000055871 00000 н
0000055998 00000 н
0000056122 00000 н
0000056257 00000 н
0000056413 00000 н
0000056572 00000 н
0000056753 00000 н
0000056915 00000 н
0000057105 00000 н
0000057235 00000 н
0000057434 00000 н
0000057549 00000 н
0000057682 00000 н
0000057890 00000 н
0000058083 00000 н
0000058217 00000 н
0000058342 00000 н
0000058456 00000 н
0000058575 00000 н
0000058709 00000 н
0000003156 00000 н
трейлер
]/предыдущая 1238033>>
startxref
0
%%EOF
946 0 объект
>поток
hV lUn-mqwk;Ƅ1PB&[3ئйc
Д.
7
%
804 0 объект
>
эндообъект
внешняя ссылка
804 143
0000000016 00000 н
0000004567 00000 н
0000004729 00000 н
0000005080 00000 н
0000005599 00000 н
0000006435 00000 н
0000006485 00000 н
0000006539 00000 н
0000006740 00000 н
0000006923 00000 н
0000007856 00000 н
0000008818 00000 н
0000008999 00000 н
0000009515 00000 н
0000009707 00000 н
0000009865 00000 н
0000010229 00000 н
0000011079 00000 н
0000011270 00000 н
0000011464 00000 н
0000027887 00000 н
0000028841 00000 н
0000037268 00000 н
0000043135 00000 н
0000043193 00000 н
0000043300 00000 н
0000043388 00000 н
0000043521 00000 н
0000043672 00000 н
0000043810 00000 н
0000043943 00000 н
0000044083 00000 н
0000044230 00000 н
0000044378 00000 н
0000044523 00000 н
0000044632 00000 н
0000044738 00000 н
0000044840 00000 н
0000045008 00000 н
0000045103 00000 н
0000045200 00000 н
0000045305 00000 н
0000045405 00000 н
0000045506 00000 н
0000045621 00000 н
0000045721 00000 н
0000045825 00000 н
0000045972 00000 н
0000046125 00000 н
0000046246 00000 н
0000046404 00000 н
0000046554 00000 н
0000046699 00000 н
0000046796 00000 н
0000046904 00000 н
0000047064 00000 н
0000047161 00000 н
0000047269 00000 н
0000047429 00000 н
0000047582 00000 н
0000047702 00000 н
0000047899 00000 н
0000048010 00000 н
0000048119 00000 н
0000048268 00000 н
0000048379 00000 н
0000048487 00000 н
0000048613 00000 н
0000048733 00000 н
0000048830 00000 н
0000048998 00000 н
0000049106 00000 н
0000049228 00000 н
0000049335 00000 н
0000049444 00000 н
0000049595 00000 н
0000049744 00000 н
0000049852 00000 н
0000050010 00000 н
0000050158 00000 н
0000050300 00000 н
0000050419 00000 н
0000050535 00000 н
0000050674 00000 н
0000050824 00000 н
0000050919 00000 н
0000051073 00000 н
0000051184 00000 н
0000051360 00000 н
0000051529 00000 н
0000051625 00000 н
0000051806 00000 н
0000051901 00000 н
0000052051 00000 н
0000052159 00000 н
0000052267 00000 н
0000052375 00000 н
0000052489 00000 н
0000052586 00000 н
0000052735 00000 н
0000052879 00000 н
0000053034 00000 н
0000053132 00000 н
0000053241 00000 н
0000053358 00000 н
0000053473 00000 н
0000053636 00000 н
0000053785 00000 н
0000053921 00000 н
0000054082 00000 н
0000054231 00000 н
0000054421 00000 н
0000054578 00000 н
0000054695 00000 н
0000054836 00000 н
0000054944 00000 н
0000055177 00000 н
0000055290 00000 н
0000055402 00000 н
0000055524 00000 н
0000055637 00000 н
0000055749 00000 н
0000055871 00000 н
0000055998 00000 н
0000056122 00000 н
0000056257 00000 н
0000056413 00000 н
0000056572 00000 н
0000056753 00000 н
0000056915 00000 н
0000057105 00000 н
0000057235 00000 н
0000057434 00000 н
0000057549 00000 н
0000057682 00000 н
0000057890 00000 н
0000058083 00000 н
0000058217 00000 н
0000058342 00000 н
0000058456 00000 н
0000058575 00000 н
0000058709 00000 н
0000003156 00000 н
трейлер
]/предыдущая 1238033>>
startxref
0
%%EOF
946 0 объект
>поток
hV lUn-mqwk;Ƅ1PB&[3ئйc
Д. Z:0A2@3A Lb
Z:0A2@3A Lb
Горизонтальная циркуляция по поверхностям плотности вносит существенный вклад в долгосрочную среднюю меридиональную опрокидывающую циркуляцию в северной части Атлантического океана
Брокер, В.С., Питит, Д.М. и Ринд, Д. Имеет ли система океан-атмосфера более одного стабильного режима работы? Природа 315 , 21–26 (1985).
КАС Статья Google Scholar
Манабе, С.и Стоуффер, Р. Дж. Реакция совместной модели океана и атмосферы на поступление пресной воды: сравнение с событием позднего дриаса. Палеоокеанография 12 , 321–336 (1997).
Артикул Google Scholar
Rahmstorf, S. Циркуляция океана и климат за последние 120 000 лет. Природа 419 , 207–214 (2002).
КАС Статья Google Scholar
Чжан, Р. и др. Обзор роли атлантической меридиональной опрокидывающей циркуляции в многодесятилетней изменчивости Атлантики и связанных с ней климатических воздействий. Ред. Геофиз. 57 , 316–375 (2019).
и др. Обзор роли атлантической меридиональной опрокидывающей циркуляции в многодесятилетней изменчивости Атлантики и связанных с ней климатических воздействий. Ред. Геофиз. 57 , 316–375 (2019).
Артикул Google Scholar
Цезарь, Л., Рамсторф, С., Робинсон, А., Фейлнер, Г. и Саба, В. Наблюдаемый отпечаток ослабевающей перевернутой циркуляции Атлантического океана. Природа 556 , 191–196 (2018).
КАС Статья Google Scholar
Chen, X. & Tung, K.K. Глобальное поверхностное потепление, усиленное слабой опрокидывающей циркуляцией Атлантики. Природа 559 , 387–391 (2018).
КАС Статья Google Scholar
Бродо, Л. и Кенигк, Т. Угасание глубоководной конвекции северного океана в совокупности имитационных моделей климата 20-го и 21-го веков. Клим. Динамика 46 , 2863–2882 (2016).
Клим. Динамика 46 , 2863–2882 (2016).
Артикул Google Scholar
Heuzé, C. Североатлантическое глубоководное образование и AMOC в моделях CMIP5. Науки об океане. 13 , 609–622 (2017).
Артикул Google Scholar
Диксон, Р. Р. и Браун, Дж. Производство глубоководных вод Северной Атлантики: источники, скорости и пути. Ж. Геофиз. Res.: Oceans 99 , 12319–12342 (1994).
Артикул Google Scholar
Денглер М., Фишер Дж., Шотт Ф. А. и Зантопп Р. Глубинное Лабрадорское течение и его изменчивость в 1996–2005 гг. Геофиз. Рез. лат. 33 , 1–5 (2006).
Артикул Google Scholar
Пикарт, Р. С. и Сполл, М.А. Влияние конвекции Лабрадорского моря на меридиональную опрокидывающую циркуляцию в Северной Атлантике. J. Phys. океаногр. 37 , 2207–2227 (2007).
J. Phys. океаногр. 37 , 2207–2227 (2007).
Артикул Google Scholar
Сарафанов А. и др. Средняя полноводная летняя циркуляция и переносы на северной периферии Атлантического океана в 2000-е гг. Ж. Геофиз. Res.: Oceans 117 , 1–22 (2012).
Google Scholar
Хольте, Дж. и Странео, Ф. Сезонное опрокидывание Лабрадорского моря, наблюдаемое с помощью поплавков Арго. J. Phys. океаногр. 47 , 2531–2543 (2017).
Артикул Google Scholar
Россби, Т., Ревердин, Г., Чафик, Л. и Сёйланд, Х. Прямая оценка направленных к полюсу объемов, тепла и потоков пресной воды на 59,5 северной широты между Гренландией и Шотландией. Ж. Геофиз. Рез.: Океаны 122 , 5870–5887 (2017).
Артикул Google Scholar
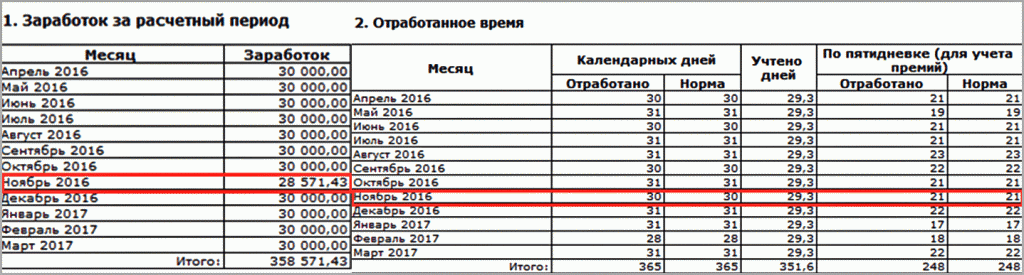
Чафик, Л. и Россби, Т. Объем, тепло и дивергенция пресной воды в субполярной части Северной Атлантики предполагают, что северные моря являются ключом к состоянию меридиональной опрокидывающей циркуляции. Геофиз. Рез. лат. 46 , 4799–4808 (2019).
Артикул Google Scholar
Lozier, M.S. et al. Кардинальное изменение нашего взгляда на переворот в субполярной части Северной Атлантики. Наука 363 , 516–521 (2019).
КАС Статья Google Scholar
Зоу, С., Лозиер, М.С., Ли, Ф., Абернати, Р. и Джексон, Л. Опрокидывание с компенсацией плотности в Лабрадорском море. Нац. Geosci. 13 , 121–126 (2020).
КАС Статья Google Scholar
Лампкин Р. и Спир К.Крупномасштабная вертикальная и горизонтальная циркуляция в северной части Атлантического океана. J. Phys. океаногр. 33 , 1902–1920 (2003).
J. Phys. океаногр. 33 , 1902–1920 (2003).
Артикул Google Scholar
Olsson, K.A. et al. Промежуточная вода Гренландского моря в канале Фарерской отмели: распространение выброса гексафторида серы. Deep-Sea Res. Часть I 52 , 279–294 (2005).
КАС Статья Google Scholar
Бракстад А., Воге К., Хавик Л. и Мур Г. В. К. Трансформация водных масс в Гренландском море в период 1986–2016 гг. J. Phys. океаногр. 49 , 121–140 (2019).
Артикул Google Scholar
Рудельс Б. Термохалинная циркуляция Северного Ледовитого океана и Гренландского моря. Филос. Транс. Р. Соц. А: Физ. англ. науч. 352 , 287–299 (1995).
Google Scholar
Mauritzen, C. Производство плотных переливных вод, питающих Северную Атлантику через Гренландско-Шотландский хребет. Часть 1: Доказательства пересмотренной схемы распространения. Deep-Sea Res. Часть I 43 , 769–806 (1996).
Часть 1: Доказательства пересмотренной схемы распространения. Deep-Sea Res. Часть I 43 , 769–806 (1996).
Артикул Google Scholar
Rudels, B., Quadfasel, D. & Friedrich, H. Глубоководный компонент Северного Ледовитого океана в переливе Гренландия-Шотландия. Кооперативный рез. ICES. Респ. 225 , 172–194 (1998).
Google Scholar
Eldevik, T. et al. Наблюдаемые источники и изменчивость разлива северных морей. Нац. Geosci. 2 , 406–410 (2009).
КАС Статья Google Scholar
Сармьенто, Дж. Л. и Брайан, К. Модель океанического транспорта для Северной Атлантики. Ж. Геофиз. Рез.: Oceans 87 , 394–408 (1982).
Артикул Google Scholar
Райт, Д. Г., Томпсон, К. Р. и Лу, Ю. Включение многолетней гидрографической информации в модель Северной Атлантики с учетом водоворотов. Ж. Геофиз. Res.: Oceans 111 , 1–16 (2006).
Р. и Лу, Ю. Включение многолетней гидрографической информации в модель Северной Атлантики с учетом водоворотов. Ж. Геофиз. Res.: Oceans 111 , 1–16 (2006).
Google Scholar
Lee, S.K. et al. Глобальная меридиональная опрокидывающая циркуляция, полученная на основе модели океана и морского льда с ограниченными данными. Геофиз. Рез. лат. 46 , 1521–1530 (2019).
Артикул Google Scholar
Чжан, Р. и Валлис, Г.К. Роль донного вихря, растягивающегося на пути североатлантического западного пограничного течения и на северном рециркуляционном круговороте. J. Phys. океаногр. 37 , 2053–2080 (2007).
Артикул Google Scholar
Delworth, T.L. et al. Смоделированный климат и изменение климата в GFDL CM2. 5 совмещенная климатическая модель высокого разрешения. J. Климат 25 , 2755–2781 (2012).
J. Климат 25 , 2755–2781 (2012).
Артикул Google Scholar
Чжан, Р. Когерентный поверхностно-подповерхностный отпечаток атлантической меридиональной опрокидывающей циркуляции. Геофиз. Рез. лат. 35 , L20705 (2008).
Артикул Google Scholar
Чжан, Р. и др. Чувствительность циркуляции Северной Атлантики к резкому изменению стока Северного моря в глобальной связанной модели климата высокого разрешения. Ж. Геофиз. Res.: Oceans 116 , 1–14 (2011).
Google Scholar
Менари, М. Б., Джексон, Л. К. и Лозье, М. С. Согласование взаимосвязи между AMOC и Лабрадорским морем в наблюдениях OSNAP и климатических моделях. Геофиз.Рез. лат. 47 , e2020GL089793 (2020).
Google Scholar

Hirschi, J. & Marotzke, J. Реконструкция меридиональной опрокидывающей циркуляции по граничным плотностям и зональному напряжению ветра. J. Phys. океаногр. 37 , 743–763 (2007).
Артикул Google Scholar
McCarthy, G.D. et al. Измерение меридиональной опрокидывающей циркуляции Атлантики на 26° северной широты. Прог. океаногр. 130 , 91–111 (2015).
Артикул Google Scholar
McCarthy, G.D. et al. Устойчивые наблюдения АМОК: методология и технология. Ред. Геофиз. 58 , e2019RG000654 (2020).
Артикул Google Scholar
Яшаяев И. и Лодер Дж. В. Дальнейшая интенсификация глубоководной конвекции в Лабрадорском море в 2016 г. Геофиз. Рез. лат. 44 , 1429–1438 (2017).
Артикул Google Scholar
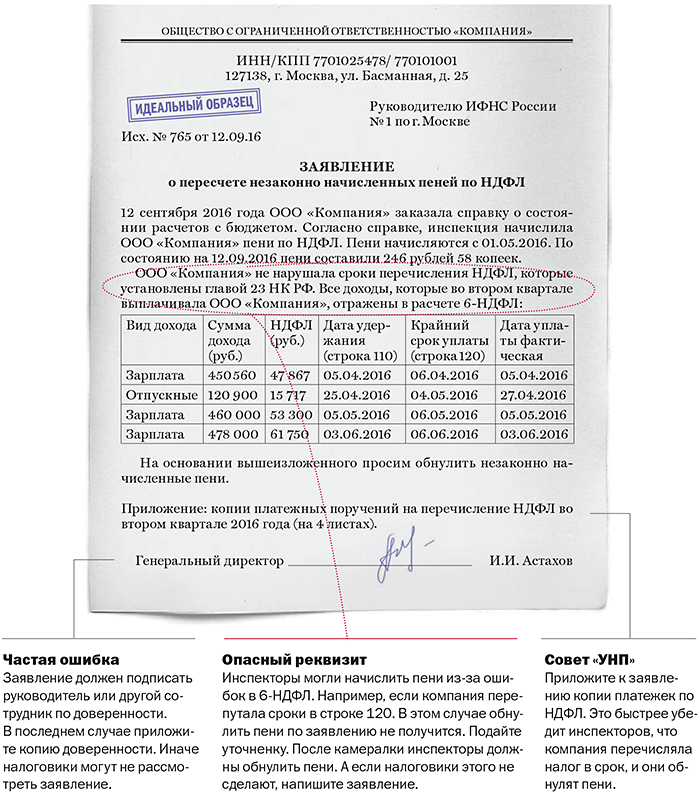
Зоу, С., Бауэр, А., Фьюри, Х., Лозиер, М.С. и Сюй, X. Перерисовка путей перелива Исландия-Шотландия в Северной Атлантике. Нац. коммун. 11 , 1–8 (2020).
Google Scholar
Harden, B.E. et al. Источники переполнения Датского пролива вверх по течению: наблюдения с причальной группы с высоким разрешением. Deep-Sea Res. Часть I 112 , 94–112 (2016).
Артикул Google Scholar
Хансен, Б., Ларсен, К. М. Х., Хатун, Х. и Остерхус, С. Стабильное переполнение канала Фарерского берега, 1995–2015 гг. Науки об океане. 12 , 1205–1220 (2016).
Артикул Google Scholar
Østerhus, S. et al. Арктические средиземноморские обмены: согласованный бюджет объемов и тенденции переносов за два десятилетия наблюдений. Науки об океане. 15 , 379–399 (2019).
Артикул Google Scholar
Аагард, К., Свифт, Дж. Х. и Кармак, Э. К. Термохалинная циркуляция в арктических средиземноморских морях. Ж. Геофиз. Res.: Oceans 90 , 4833–4846 (1985).
Артикул Google Scholar
Бещинска-Мёллер А., Вудгейт Р. А., Ли К., Меллинг Х. и Карчер М. Синтез обменов через основные океанические ворота в Северный Ледовитый океан. Океанография 24 , 82–99 (2011).
Артикул Google Scholar
Чафик Л. и др. Открытие неизвестного пути, несущего переливные воды к каналу Фарерского берега. Нац. коммун. 11 , 1–10 (2020).
Артикул КАС Google Scholar
Россби, Т., Флэгг, К., Чафик, Л., Харден, Б. и Сойланд, Х. Прямая оценка объема, тепла и обмена пресной водой через Гренландско-Исландско-Фарерско-Шотландский хребет.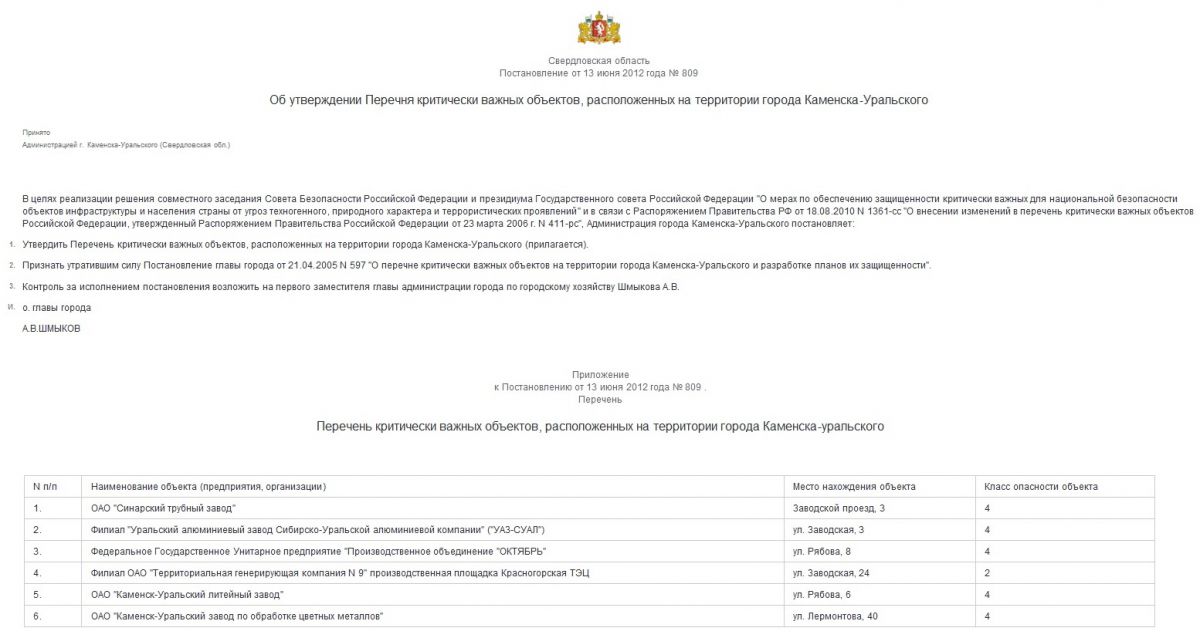 Ж. Геофиз. Рез.: Океаны 123 , 7139–7153 (2018).
Ж. Геофиз. Рез.: Океаны 123 , 7139–7153 (2018).
Артикул Google Scholar
Де Стеур, Л., Хансен, Э., Мауритцен, К., Бещинска-Мёллер, А. и Фарбах, Э. Воздействие рециркуляции на Восточно-Гренландское течение в проливе Фрама: результаты заякоренного измерителя течений замеры с 1997 по 2009 год. Deep-Sea Res. Часть I 92 , 26–40 (2014).
Артикул Google Scholar
Petit, T., Lozier, M.S., Josey, S.A. & Cunningham, S.A. Формирование глубоководных слоев Атлантического океана происходит главным образом в Исландском бассейне и море Ирмингера за счет местного воздействия плавучести. Геофиз. Рез. лат. 47 , e2020GL0 (2020).
Артикул Google Scholar
Smedsrud, L.H. et al. Роль Баренцева моря в климатической системе Арктики. Ред.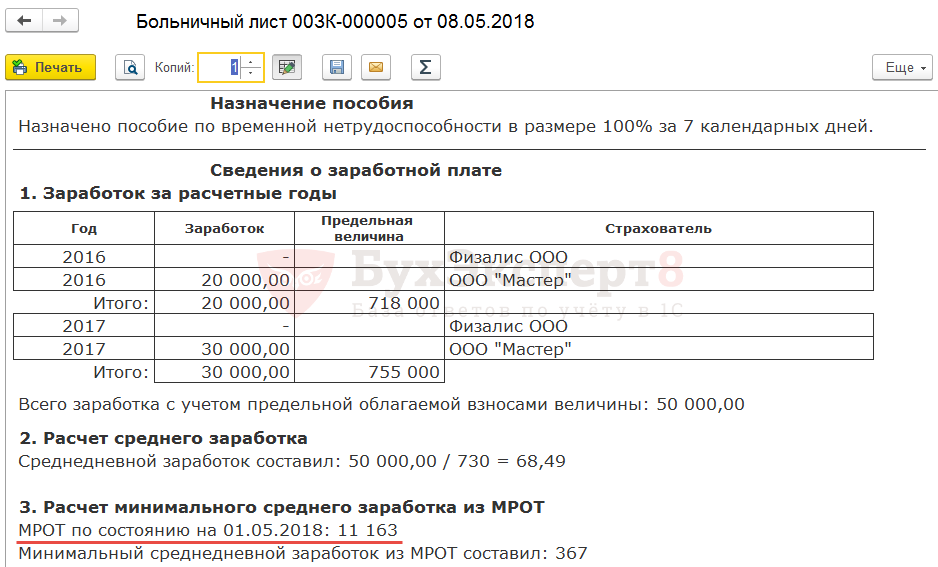 Геофиз. 51 , 415–449 (2013).
Геофиз. 51 , 415–449 (2013).
Артикул Google Scholar
Рейн, М., Штейнфельдт, Р., Кике, Д., Стендардо, И. и Яшаяев, И. Изменчивость вентиляции морской воды Лабрадора и ее влияние на кислород и антропогенный углерод: обзор. Филос. Транс. Р. Соц. A: Math., Phys. англ. науч. 375 , 20160321 (2017).
Артикул КАС Google Scholar
Томас, М. Д., Трегье, А. М., Бланке, Б., Деше, Дж. и Волдуар, А. А. Метод Лагранжа для выделения воздействия субдукции смешанных слоев на меридиональную опрокидывающую циркуляцию в численной модели. Дж. Клим. 28 , 7503–7517 (2015).
Артикул Google Scholar
Ли, Ф.и другие. Локальные и нисходящие взаимосвязи между объемом морской воды Лабрадора и изменчивостью меридиональной опрокидывающей циркуляции в Северной Атлантике.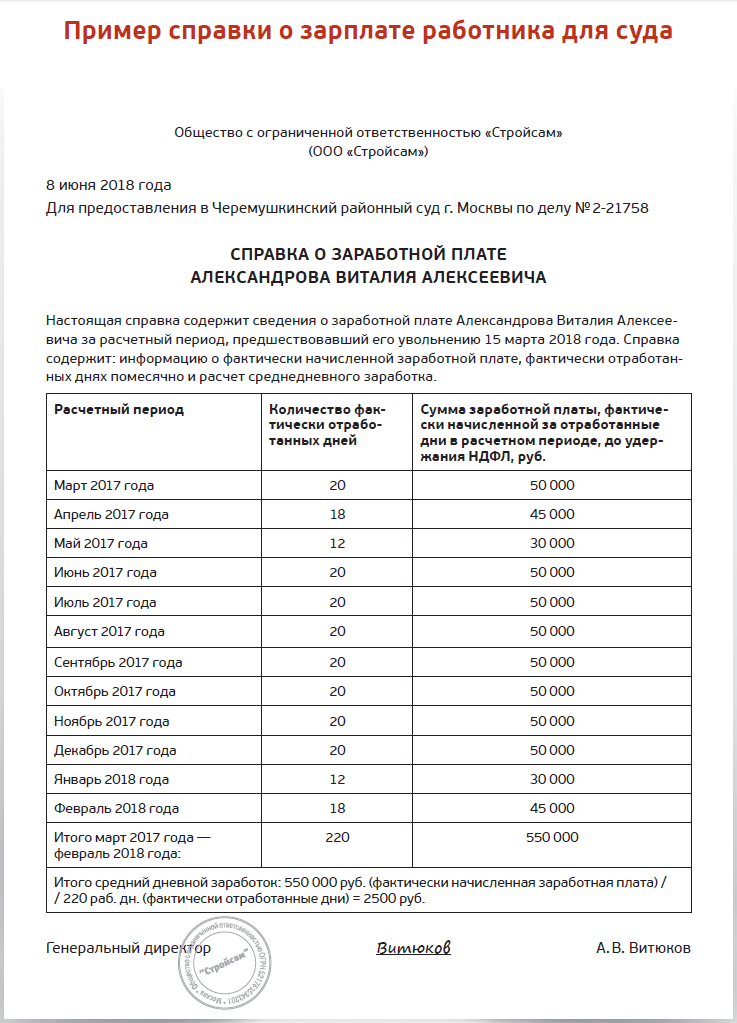 Дж. Клим. 32 , 3883–3898 (2019).
Дж. Клим. 32 , 3883–3898 (2019).
Артикул Google Scholar
Диксон, Р. Р., Майнке, Дж., Мальмберг, С. А. и Ли, А. Дж. «Большая аномалия солености» в северной части Северной Атлантики, 1968–1982 гг. Прог. океаногр. 20 , 103–151 (1988).
Артикул Google Scholar
Белкин И. М., Левитус С., Антонов Дж., Мальмберг С. А. «Большие аномалии солености» в Северной Атлантике. Прог. океаногр. 41 , 1–68 (1998).
Артикул Google Scholar
Locarnini R. A. et al. Атлас Мирового океана 2013 г., Том 1: Температура. Под ред. С. Левитуса, под ред. А. Мишонова.; Атлас NOAA NESDIS 73 , 40 стр. (2013 г.).
Zweng, M.M. et al. Атлас Мирового океана 2013 г., Том 2: Соленость. Под ред. С. Левитуса, под ред. А. Мишонова; Атлас NOAA NESDIS 74 , 39 стр. (2013).
(2013).
Риджуэй, К. Р., Данн, Дж. Р. и Уилкин, Дж. Л. Интерполяция океана методом четырехмерных наименьших квадратов – Применение к водам вокруг Австралии. Дж Атмос. Океан. Тех. 19 , 1357–1375 (2002).
Артикул Google Scholar
Данн, Дж. Р. и Риджуэй, К. Р. Картирование свойств океана в регионах со сложной топографией. Deep Sea Resh Часть I Oceanogr. Рез. 49 , 591–604 (2002).
КАС Статья Google Scholar
Dee, D. P. et al. Реанализ ERA-Interim: конфигурация и производительность системы усвоения данных. QJR Meteorol. соц. 137 , 553–597 (2011).
Артикул Google Scholar
Griffies, S.M. et al. Вклад OMIP в CMIP6: экспериментальный и диагностический протокол для физического компонента проекта взаимного сравнения моделей океана. Геофизика. Модель Дев. 9 , 3231–3296 (2016).
Геофизика. Модель Дев. 9 , 3231–3296 (2016).
Артикул Google Scholar
Rio, M.H., Mulet, S. & Picot, N. Beyond GOCE для оценки циркуляции океана: синергетическое использование альтиметрии, гравиметрии и данных на месте дает новое понимание геострофических течений и течений Экмана. Геофиз. Рез. лат. 41 , 8918–8925 (2014).
Артикул Google Scholar
Lozier, M. S. et al. Меридиональная опрокидывающая циркуляция и связанный с ней перенос тепла и пресной воды, наблюдаемые с помощью массива OSNAP (Опрокидывание в субполярной программе Северной Атлантики) с 2014 по 2016 год.Цифровой репозиторий Герцога. https://doi.org/10.7924/r4z60gf0f (2019 г.).
Li, F., Lozier, M.S. & Johns, W.E. Расчет меридионального объема, переноса тепла и пресной воды из системы наблюдения в субполярной части Северной Атлантики: эксперимент по моделированию системы наблюдения.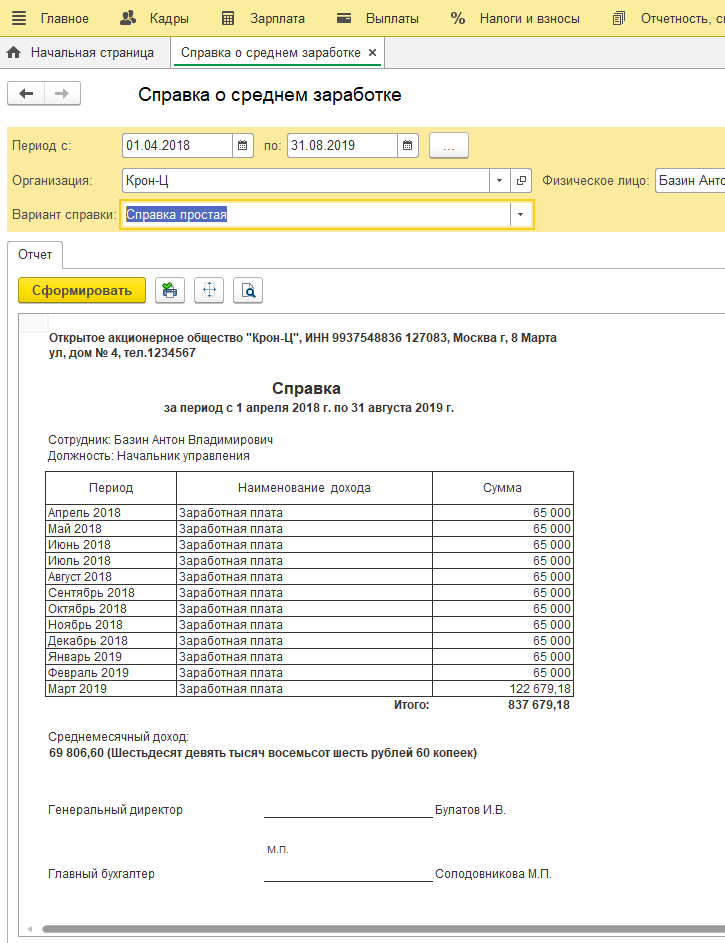 Дж. Атмос. Океан. Тех. 34 , 1483–1500 (2017).
Дж. Атмос. Океан. Тех. 34 , 1483–1500 (2017).
Артикул Google Scholar
Карри Б., Ли К.М., Петри Б., Мориц Р. Э. и Квок Р. Многолетний объем, перенос жидкой пресной воды и морского льда через пролив Дэвиса, 2004–2010 гг. J. Phys. океаногр. 44 , 1244–1266 (2014).
Артикул Google Scholar
Данабасоглу, Г., Лардж, В. Г. и Бриглеб, Б. П. Воздействие параметризованных разливов Северного моря на климат. Ж. Геофиз. Res.: Oceans 115 , 1–29 (2010).
Google Scholar
Ван, Х., Легг, С. А. и Холлберг, Р. В. Представление разливов северных морей и их крупномасштабного воздействия на климат в связанных моделях. Моделирование океана 86 , 76–92 (2015).
Артикул Google Scholar
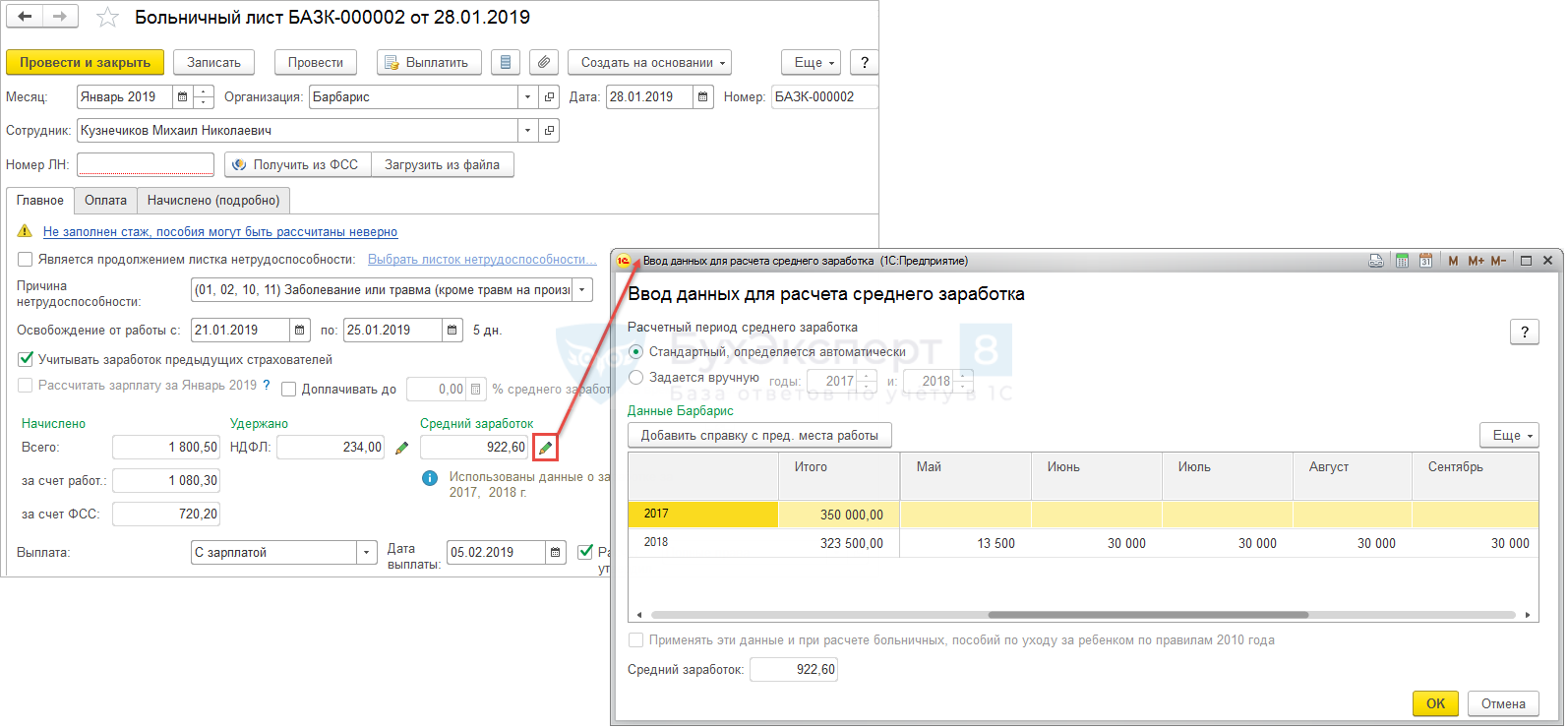
Чжан, Р. и Томас, М. Подтверждающие данные для «Горизонтальная циркуляция по поверхностям плотности вносит существенный вклад в долгосрочную среднюю меридиональную опрокидывающую циркуляцию в северной Атлантике» [набор данных].Зенодо. https://doi.org/10.5281/zenodo.45
(2021 г.).
McCartney, M.S. & Talley, L.D. Преобразование теплой воды в холодную в северной части Северной Атлантики. J. Phys. океаногр. 14 , 922–935 (1984).
Артикул Google Scholar
Важность временного разрешения данных (Журнал экспериментальной биологии 215 (922-933))
933 Биомеханика соответствует экологической нише
Buckley, L.B., Urban, M.C., Angilletta, M.J., Crozier, L.G., Rissler, L.J. и
Sears, M.W. (2010). Может ли механизм формировать модели распространения видов? Экол.
Письмо. 13, 1041-1054.
Денни М.В., Миллер Л.П. и Харли С.Д.Г. (2006). Термическая нагрузка на приливные
блюдечки: долгосрочные ретроспективные прогнозы и пределы летальности. Дж. Эксп. биол. 209, 2420-2431.
Дж. Эксп. биол. 209, 2420-2431.
Диллон, М.Е., Ван, Г. и Хьюи, Р.Б. (2010). Глобальные метаболические последствия недавнего
потепления климата.Природа 467, 704-706.
Дорманн, К.Ф., Шимански, С.Дж., Кабрал, Дж., Чуйне, И., Грэм, К.Х., Хартиг,
Ф., Кирни, М.Р., Морин, X., Ремерманн, К., Шредер, Б. и др. др. (2012).
Корреляция и процесс в моделях распространения видов: преодоление дихотомии. Ж.
Биогеогр. doi:10.1111/j.1365-2699.2011.02659.x.
Данэм, А. Е. (1993). Реакция населения на изменение окружающей среды: оперативная среда
, физиологически структурированные модели и динамика населения.В Biotic
Interactions and Global Change (изд. PM Kareiva, JG Kingsolver и RB
Huey), стр. 95-119. Сандерленд, Массачусетс: Sinauer Associates.
Эренбергер, Дж. К. (2010). Физиологические реакции ящериц на температуру,
Sceloporus undulatus. Кандидатская диссертация, Университет штата Индиана, Терре-Хот, Индиана.
Элит, Дж. и Литвик, Дж. Р. (2009). Модели распространения видов: экологическое
объяснение и предсказание в пространстве и времени.Анну. Преподобный Экол. Эвол. Сист. 40,
677-697.
Элит, Дж., Кирни, М.Р. и Филлипс, С.Дж. (2010). Искусство моделирования ареалов
видов. Методы Экол. Эвол. 1, 330-342.
Фодри, Ф.Дж., Хек, К.Л., Пауэрс, С.П., Грэм, В.М. и Робинсон, К.Л.
(2010). Связанные с климатом десятилетние изменения сообществ
рыб, связанных с водорослями, в северной части Мексиканского залива. Глоб. Изменить биол. 16, 48-59.
Гилман, С.Э., Уэти Д.С. и Хельмут Б. (2006). Изменение чувствительности температуры тела организма
к изменению климата в локальном и географическом масштабах.
Проц. Натл. акад. науч. США 103, 9560-9565.
Грант, Б.В. и Портер, В.П. (1992). Моделирование глобальных макроклиматических ограничений на
эктотермных энергетических балансов. Являюсь. Зоол. 32, 154-178.
Хельмут, Б. (2009). От клеток до береговых линий: как мы можем использовать физиологию для прогнозирования
последствий изменения климата? Дж.Эксп. биол. 212, 753-760.
Хельмут Б., Кингсолвер Дж. Г. и Кэррингтон Э. (2005). Биофизика, физиологическая
экология и изменение климата: имеет ли значение механизм? Анну. Преподобный Физиол. 67, 177-
201.
Helmuth, B., Broitman, B.R., Yamane, L., Gilman, S.E., Mach, K., Mislan, K.A.S.
и Denny, M.W. (2010). Климатология организма: анализ изменчивости окружающей среды
в масштабах, соответствующих физиологическому стрессу. Дж. Эксп. биол. 213, 995-1003.
Хельмут Б., Ямане Л., Лалвани С., Матцелле А., Токштейн А. и Гао Н.
(2011). Скрытые сигналы изменения климата в приливно-отливных экосистемах: чего (не)до
ожидать, когда ждешь. Дж. Эксп. Мар биол. Экол. 400.
Хьюи, Р. Б. (1991). Физиологические последствия выбора среды обитания. Являюсь. Нац. 137,
S91-S115.
Хьюи, Р. Б., Петерсон, С. Р., Арнольд, С. Дж. и Портер, В. П. (1989). Горячие камни и
не очень горячие камни: выбор места отступления подвязочными змеями и его термические
последствия.Экология 70, 931-944.
Хатчинс, Л. В. (1947). Основания для температурного зонирования в географическом распределении
. Экол. моногр. 17, 325-335.
Джонс, С.Дж., Мешковска, Н. и Уэти, Д.С. (2009). Связь температурных допусков
и биогеографии: Mytilus edulis (L.) на его южной границе на восточном побережье
Соединенных Штатов. биол. Бык. 217, 325-335.
Кирни, М. Р. (2006). Среда обитания, окружающая среда и ниша: что мы моделируем? Ойкос
115, 186-191.
Кирни, М. Р. (2012). Метаболическая теория, история жизни и распространение земных
экзотерм. Функц. Экол. 26, 167-179.
Кирни, М. Р. и Портер, В. П. (2004). Картирование фундаментальной ниши: физиология,
климат и распространение ночной ящерицы. Экология 85, 3119-3131.
Экология 85, 3119-3131.
Кирни, М. Р. и Портер, В. П. (2006). Экологи уже начали восстанавливать экологию сообщества
по функциональным признакам. Тенденции Экол.Эвол. 21, 481-482.
Кирни, М. Р. и Портер, В. П. (2009). Моделирование механистической ниши: объединение
физиологических и пространственных данных для прогнозирования ареалов видов. Экол. лат. 12, 334-350.
Kearney, M.R., Porter, W.P., Williams, C.K., Ritchie, S.A. и Hoffmann, A.A.
(2009a). Интеграция биофизических моделей и эволюционной теории для прогнозирования климатических воздействий
на ареалы видов: комар денге Aedes aegypti в Австралии. Функц.
Экол.23, 528-538.
Кирни, М.Р., Филлипс, Б.Л., Трейси, Ч.Р., Кристиан, К., Беттс, Г. и Портер, В.
С. (2008). Моделирование распределения видов без использования распределения видов: тростниковая жаба
в Австралии в нынешних и будущих климатических условиях. Экография 31, 423-434.
Кирни, М. Р., Шайн, Р. и Портер, В. П. (2009b). Потенциал поведенческой терморегуляции
Р., Шайн, Р. и Портер, В. П. (2009b). Потенциал поведенческой терморегуляции
для защиты «хладнокровных» животных от потепления климата. проц.
Нац.акад. науч. США 106, 3835-3840.
Кирни, М. Р., Симпсон, С. Дж., Раубенхаймер, Д. и Хельмут, Б. (2010a).
Моделирование экологической ниши по функциональным признакам. Филос. Транс. Р. Соц. Лонд. B
Биол. науч. 365, 3469-3483.
Кирни, М. Р., Уинтл, Б. А. и Портер, В. П. (2010b). Коррелятивные и механистические
модели распространения видов обеспечивают конгруэнтные прогнозы в условиях изменения климата
Сохран. лат. 3, 203-213.
Лика К., Kearney, M.R., Frietas, V., van der Veer, HW, van der Meer, J.,
Wijsman, J.W.M., Pecquerie, L. and Kooijman, S.A.L.M. (2011a). «Ковариационный метод»
для оценки параметров стандартной динамической энергетической
бюджетной модели. Я: философия и подход. Дж. Си Рез. 66, 270-277.
Лика К., Кирни М. Р. и Коойман С. А. Л. М. (2011b). «Ковариационный метод»
А. Л. М. (2011b). «Ковариационный метод»
для оценки параметров стандартной модели динамического энергетического баланса.II:
свойства и предварительные модели. Дж. Си Рез. 66, 278-288.
Макартур, Р. и Левинс, Р. (1967). Предельное сходство, конвергенция и дивергенция сосуществующих видов. Являюсь. Нац. 101, 377-385.
Магуайр, Б., младший (1973). Структура отклика ниши и аналитические возможности ее связи со средой обитания. Являюсь. Нац. 107, 213-246.
Маккалоу, Э. К. и Портер, В. П. (1971). Вычисление спектра солнечного излучения
в ясный день для земной экологической среды.Экология 52, 1008-1015.
Макгилл, Б. Дж., Энквист, Б. Дж., Вейхер, Э. и Вестоби, М. (2006). Восстановление экологии сообщества
по функциональным признакам. Тенденции Экол. Эвол. 21, 178-185.
Мезингер Ф., ДиМего Г., Калнай Э., Митчелл К., Шафран П.С., Эбисузаки В.,
Джови Д., Вуллен Дж., Роджерс Э., Бербери, ЭХ и др. (2006). Североамериканский
Региональный повторный анализ. Бык. Являюсь. Метеор. соц. 87, 343-360.
Бык. Являюсь. Метеор. соц. 87, 343-360.
Мислан, К. А. С. и Уэти, Д.С. (2011). Метеорологические данные с координатной привязкой как ресурс
для механистической макроэкологии в прибрежной среде. Экол. заявл. 21,
2678-2690.
Монако, Си Джей и Хельмут, Б. (2011). Переломные моменты, пороги и ключевая роль физиологии в исследованиях изменения морского климата. Доп. Мар биол. 60, 123-160.
Мамби, П. Дж., Иглесиас-Прието, Р., Хутен, А. Дж., Сейл, П. Ф., Хоег-Гулдберг, О.,
Эдвардс, А. Дж., Харвелл, К. Д., Гомес, Э.D., Knowlton, N., Hatziolos, M.E. et al.
(2011). Пересмотр климатических порогов и коллапс экосистемы. Фронт. Экол. Окружающая среда.
9, 94-96.
Натори, Ю. и Портер, В.П. (2007). Японский сероу (Capricornis crispus) Energys
Ландшафтное моделирование прогнозирует распространение на Хонсю, Япония. Экол. заявл. 17, 1441-
1459.
Niewiarowski, P.H., Angilletta, MJ, Jr и Leache, A.D. (2004). Филогенетический
Филогенетический
сравнительный анализ изменчивости жизненного цикла популяций ящерицы
Sceloporus undulatus: пример и прогноз.Эволюция 58, 619-633.
Нисбет, Р. М., Юсуп, М., Кланьшек, Т. и Пекери, Л. (2012). Интеграция
теории динамического энергетического баланса (DEB) с традиционными биоэнергетическими моделями. Дж. Эксп.
Биол. 215, 892-902.
Паркер, С. и Эндрюс, Р. (2007). Температура инкубации и фенотипические признаки
Sceloporus undulatus: последствия для северных пределов распространения. Экология
151, 218-231.
Павлин, С. (2011). Прогнозируемое изменение климата в 21 веке для мест обитания росомах
на территории Соединенных Штатов.Окружающая среда. Рез. лат. 6, 014007.
Porter, WP (1989). Новые модели животных и эксперименты по расчету потенциала роста
на разных высотах. Физиол. Зоол. 62, 286-313.
Портер, В.П. и Митчелл, Дж.В. (2006).
Метод и система расчета пространственно-временного воздействия климата и других условий среды на животных.
Публикация заявки на патент США, доступна по адресу
www.patentstorm.us/patents/7155377-fulltext.HTML.
Портер В.П., Митчелл Дж.В., Бекман В.А. и ДеВитт С.Б. (1973). Поведенческие
последствия механистической экологии – тепловое и поведенческое моделирование пустынных
эктотермов и их микроокружения. Экология 13, 1-54.
Портер В.П., Будараю С., Стюарт В.Е. и Раманкутти Н. (2000). Расчет
воздействия климата на птиц и млекопитающих: воздействие на биоразнообразие, сохранение,
параметры популяции и глобальную структуру сообщества.Являюсь. Зоол. 40, 597-630.
Портер, В.П., Сабо, Дж.Л., Трейси, К.Р., Райхман, О.Дж. и Раманкутти, Н.
(2002). Физиология в ландшафтном масштабе: взаимодействие растений и животных. интегр. Комп.
Биол. 42, 431-453.
Портер, В.П., Вахария, Н.П., Клузи, В.Д. и Даффи, Д. (2006). Poʼouli
Ландшафтные биоинформатические модели предсказывают энергетику, поведение, рацион и распределение
на Мауи. интегр. Комп. биол. 46, 1143-1158.
интегр. Комп. биол. 46, 1143-1158.
Рут, Т.(1988). Энергетические ограничения на распространение и численность птиц. Экология
69, 330-339.
Рафгарден, Дж. (1972). Эволюция ширины ниши. Являюсь. Нац. 106, 683-718.
Savage, VM (2004). Улучшенные приближения к отношениям масштабирования для видов,
популяций и экосистем в зависимости от широты и высоты. Дж. Теор.
Биол. 227, 525-534.
Шёнер, Т. В. (1986). Механистические подходы к экологии сообществ: новый редукционизм? Являюсь.Зоол. 26, 81-106.
Синерво, Б., Мендес-де-ла-Крус, Ф., Майлз, Д.Б., Хеулин, Б., Бастиан, Э.,
Виллагран-Санта-Крус, М., Лара-Ресендис, Р., Мартинес -Mendez, N., Calderon-
Espinosa, ML, Meza-Lazaro, RN et al. (2010). Эрозия разнообразия ящериц из-за
изменения климата и изменения тепловых ниш. Наука 328, 894-899.
Соберон, Дж. (2007). Гриннельские и эльтонские ниши и географическое распространение
видов. Экол. лат. 10, 1115-1123.
10, 1115-1123.
Тинкль, Д. В. и Данэм, А. Э. (1986). Сравнительные истории жизни двух синтопных
сцелопориновых ящериц. Копия 1986, 1-18.
Ван дер Меер, Дж. (2006). Метаболические теории в экологии. Тенденции Экол. Эвол. 21, 136-
140.
Виолле, К., Навас, М.-Л., Виле, Д., Казаку, Э., Фортунель, К., Хаммель, И. и
, Гарнье, Э. ( 2007). Пусть понятие черты будет функциональным! Ойкос 116, 882-892.
Уильямс, С. Э., Шу, Л.П., Исаак Дж. Л., Хоффманн А. А. и Лэнгхэм Г. (2008).
На пути к интегрированной системе оценки уязвимости видов к
изменению климата. PLoS биол. 6, е325.
Уинтл, Б.А., Маккарти, Массачусетс, Пэррис, К. и Бургман, Массачусетс (2004). Точность и
погрешность методов оценки вероятностей обнаружения точечных съемок. Экол. заявл. 14,
703-712.
Важность вертикального разрешения в свободной тропосфере для моделирования межконтинентальных шлейфов
Andreae, M.О., Броуэлл, Э.В., Гарстанг, М., Грегори, Г.Л., Харрисс, Р.К., Hill, G.F., Jacob, D.J., Pereira, M.C., Sachse, G.W., Setzer, a. В., Диас, П.Л.С., Талбот, Р.В., Торрес, А.Л., и Вофси, С.К.: Выбросы от сжигания биомассы и связанные с ними слои тумана над Амазонии, Дж. Геофиз. Res., 93, 1509–1527, https://doi.org/10.1029/JD093iD02p01509, 1988.
Balaji, V.: Вычисление климата: состояние дел, Comput. науч. Англ., 17, 9–13, https://doi.org/10.1109/MCSE.2015.109, 2015.
Бей, И., Джейкоб, Д. Дж., Янтоска, Р. М., Логан, Дж. А., Филд, Б. Д., Фиоре, А. М., Ли, К., Лю, Х.Ю., Микли, Л.Дж., и Шульц, М.Г.: Глобальное моделирование химии тропосферы с ассимилированной метеорологией: описание модели и оценка, J. Geophys. рез.-атмосфер., 106, 23073–23095, 2001.
Брассер, Г.П. и Джейкоб, Д.Дж.: Моделирование химии атмосферы, Издательство Кембриджского университета, Кембридж, 2017 г.В., Эммонс, Л.К., Гилле, Дж.К., Эдвард, Д.П., Дитер, М.Н., Чен, Г., Олсон, Дж. Р., Коннорс В. С., Киттака К. и Хэмлин А. Дж.: Связь между измерения загрязнения в тропосфере (MOPITT) и на месте наблюдения CO на основе крупномасштабного объекта, отобранного во время TRACE-P, J. Геофиз. Res.-Atmos., 109, 1–10, https://doi.org/10.1029/2003JD004308, 2004.
Д’Исидоро, М., Маурици, А., и Тампиери, Ф.: Влияние разрешения на в относительная важность числовой и физической горизонтальной диффузии в моделирование состава атмосферы, Atmos.хим. физ., 10, 6213, https://doi.org/10.5194/acp-10-6213-2010, 2010.
Дритшель, Д. Г. и Маккивер, В. Дж.: Влияние коэффициента Прандтля на баланс в геофизическая турбулентность, J. Fluid Mech., 777, 569–590, https://doi.org/10.1017/jfm.2015.348, 2015.
Durran, D.R.: Численные методы гидродинамики: с приложениями к Геофизика, https://doi.org/10.1007/978-1-4419-6412-0, 2010.
Истхэм, С. Д. и Джейкоб, Д. модели для разрешения межконтинентального переноса химических шлейфов, Atmos.хим. Phys., 17, 2543–2553, https://doi.org/10.5194/acp-17-2543-2017, 2017.
Лаборатория геофизической гидродинамики (GFDL): Краткое руководство: Идеализированная модель конечного объема https://www.gfdl.noaa.gov/cubed-sphere-quickstart/, последний доступ: апрель 2018.
Гольдштейн, А. Х., Милле, Д. Б., Маккей, М., Джегле, Л., Горовиц, Л., Купер О., Хадман Р., Джейкоб Д. Дж., Олтманс С. и Кларк А.: Влияние Азиатские выбросы при наблюдениях в Тринидад-Хед, Калифорния, во время ITCT 2К2, Дж.Геофиз. Res.-Atmos., 109, 1–13, https://doi.org/10.1029/2003JD004406, 2004.
Хаарсма Р. Дж., Робертс М. Дж., Видейл П. Л., Кэтрин А., Белуччи А., Бао, К., Чанг, П., Корти, С., Фучкар, Н.С., Гемас, В., фон Харденберг, Дж., Хазелегер В., Кодама К., Кенигк Т., Леунг Л.Р., Лу Дж., Луо Дж.Дж., Мао, Дж., Мизелински, М.С., Мизута, Р., Нобре, П., Сато, М., Скоччимарро, Э., Земмлер Т., Смолл Дж. и фон Шторх Дж. С.: Модель высокого разрешения Проект взаимного сравнения (HighResMIP v1.0) для CMIP6, Geosci. Модель Дев., 9, 4185–4208, https://doi.org/10.5194/gmd-9-4185-2016, 2016.
Haiden, T., Janousek, M., Bidlot, J., Ferranti, L., Prates, F. , Витарт Ф., Бауэр, П., и Ричардсон, Д.С.: Оценка прогнозов ЕЦСПП, включая обновление разрешения 2016 г., ECMWF Tech. Меморандум, 792 (январь 2017 г.) [онлайн] Доступна с: http://www.ecmwf.int/sites/default/files/elibrary/2015/15275-evaluation-ecmwf-forecasts-включая-2014-2015-upgrades.pdf, 2016.
Хилд, К.Л., Джейкоб, Д. Дж., Фиоре, А. М., Эммонс, Л. К., Гилле, Дж. К., Дитер, М. Н., Уорнер, Дж., Эдвардс, Д. П., Кроуфорд, Дж. Х., Хэмлин, А. Дж., Сакс Г.В., Броуэлл Э.В., Эйвери М.А., Вэй С.А., Вестберг Д.Дж., Блейк, Д. Р., Сингх, Х. Б., Сандхольм, С. Т., Талбот, Р. В., и Фьюлберг, Х. E.: Азиатский отток и транстихоокеанский перенос окиси углерода и озона. загрязнение: интегрированный спутник, самолет и перспектива модели, Дж. Геофиз. Рез.-Атмос., 108, 4804, https://doi.org/10.1029/2003JD003507, 2003.
Хилд, К.Л., Джейкоб, Д.Дж., Парк, Р.Дж., Александр, Б., Фэрли, Т.Д., Янтоска, Р. М., и Чу, Д. А.: Транстихоокеанский транспорт азиатских антропогенные аэрозоли и их влияние на качество приземного воздуха в Соединенных Штатах Штаты, J. Geophys. Рез.-Атмос., 111, D14310, https://doi.org/10.1029/2005JD006847, 2006.
Холтон, Дж. Р.: Введение в динамическую метеорологию, Elsevier, 2004.
Хойер, С. и Хамман, Дж. Дж.: xarray: Массивы и наборы данных с маркировкой N-D в Python, J. Open Res.Softw., 5, 1–6, https://doi.org/10.5334/jors.148, 2017.
Hudman, R.C., Jacob, D.J., Cooper, O.R., Evans, M.J., Heald, C.L., Park, Р. Дж., Фехсенфельд Ф., Флок Ф., Холлоуэй Дж., Хюблер Г., Кита К., Койке М., Кондо Ю., Нойман А., Новак Дж., Олтманс С., Пэрриш Д., Робертс, Дж. М., и Райерсон, Т.: Производство озона в транстихоокеанской Азии. Шлейфы загрязнения и влияние озона на качество воздуха в Калифорнии, Дж. Геофиз. Рез. D Atmos., 109, 1–14, https://doi.org/10.1029/2004JD004974, 2004.
Huynh, HT: Схемы и ограничения для адвекции, в: Пятнадцатое Международная конференция по численным методам гидродинамики, 498–503, Springer, Berlin, 1997.
Инграм, В. Дж.: Надежность обратной связи по водяному пару: ГКМ по вертикали резолюция и формулировка, J. Clim., 15, 917–921, https://doi.org/10.1175/1520-0442(2002)015<0917:OTROTW>2.0.CO;2, 2002.
Jablonowski, C. and Williamson, D.L.: Тестовый пример бароклинной нестабильности для динамические ядра модели атмосферы, Q.Дж. Рой. Метеор. Соц., 132, 2943–2975, https://doi.org/10.1256/qj.06.12, 2006.
Яблоновски, К., Лауритцен, П., Наир, Р. Д., и Тейлор, М.: Идеализированный тест случаи для динамических ядер моделей общей циркуляции атмосферы: A предложение для летнего коллоквиума NCAR ASP 2008, 74 стр., доступно по адресу: http://www-personal.umich.edu/~cjablono/NCAR_ASP_2008_idealized_testcases_29May08.pdf (последний доступ: апрель 2018 г.), 2008.
Кент, Дж., Яблоновски, К., Уайтхед, Дж. П., и Руд, Р.Б.: Оценка Транспортные алгоритмы Tracer и влияние вертикального разрешения на Динамическое ядро конечного объема, Mon. Weather Rev., 140, 1620–1638, https://doi.org/10.1175/mwr-d-11-00150.1, 2012.
Кент, Дж., Ульрих, П.А., и Яблоновски, К.: Модель динамического ядра проект взаимного сравнения: тестовые примеры транспорта Tracer, Q. J. Roy. Метеор. Soc., 140, 1279–1293, https://doi.org/10.1002/qj.2208, 2014.
Lane, D.E., Somerville, R.C.J., и Iacobellis, S.F.: параметризации облаков и радиации к изменениям вертикального разрешения, Дж.Клим., 13, 915–922, https://doi.org/10.1175/1520-0442(2000)013<0915:SOCARP>2.0.CO;2, 2000.
Lauritzen, P.H. and Thuburn, J.: Оценка схем адвекции/транспорта использование взаимосвязанных индикаторов, диаграмм рассеивания и цифровой диагностики смешения, QJ Рой. Метеор. Soc., 138, 906–918, https://doi.org/10.1002/qj.986, 2012.
Lauritzen, P.H., Jablonowski, C., Taylor, M.A., and Nair, R.D.: Rotated Версии тестов Яблоновского для стационарного состояния и бароклинной волны: A Сравнение динамических ядер, J.Доп. Модель. Системы Земли, 2, 34 стр., https://doi.org/10.3894/james.2010.2.15, 2010.
Лян, К., Джегле, Л., Хадман, Р. К., Туркети, С., Джейкоб, Д. Дж., Эйвери, М. А., Броуэлл, Э. В., Сакс, Г. В., Блейк, Д. Р., Брюн, В., Рен, X., Коэн, Р. К., Дибб, Дж. Э., Фрид, А., Фьюлберг, Х. Э., Портер, М. Дж., Хайкес, Б.Г., Хьюи Г., Сингх Х.Б. и Веннберг П.О.: Летнее влияние Азиатское загрязнение свободной тропосферы над Северной Америкой // J. Geophys. Рез.-Атм., 112, 1–20, https://doi.org/10.1029/2006JD007919, 2007.
Лин, М., Фиоре, А. М., Горовиц, Л. В., Купер, О. Р., Найк, В., Холлоуэй, Дж., Джонсон Б.Дж., Миддлбрук А.М., Олтманс С.Дж., Поллак И.Б., Райерсон, Т. Б., Уорнер, Дж. К., Видинмайер, К., Уилсон, Дж., и Вайман, Б.: Перенос озонового загрязнения из Азии в приземный воздух над западной частью Соединенных Штатов. Штаты весной, J. Geophys. Рез.-Атм., 117, Д00В07, https://doi.org/10.1029/2011JD016961, 2012.
Лин, С.-Дж.: «Вертикально лагранжево» динамическое ядро конечного объема для Глобальные модели, понедельник.Weather Rev., 132, 2293–2307, https://doi.org/10.1175/1520-0493(2004)132<2293:AVLFDC>2.0.CO;2, 2004.
Лин, С.-Дж. и Руд, Р.Б.: Многомерный полулагранжиан в форме потока транспортные схемы, пн. Weather Rev., 124, 2046–2070, 1996.
Линдзен, Р. С. и Фокс-Рабиновиц, М.: Постоянная вертикальная и горизонтальная Резолюция, пн. Weather Rev., 117, 2575–2583, https://doi.org/10.1175/1520-0493(1989)117<2575:CVAHR>2.0.CO;2, 1989.
Long, M., Eastham, S., Zhuang, J., Янтоска Р., Сульприцио М., Лундгрен Э., Мартин Р., Ауэр Б. и Томпсон М.: Начиная с IGC7?: Высокая производительность GEOS-Chem (GCHP) и Flexible Chemistry (FlexChem), 8-я Международная выставка. ГЕОС-Хим Встреча. (IGC8), Гарвардский ун-т. 2017, доступно по адресу: http://acmg.seas.harvard.edu/presentations/IGC8/talks/MonA_Overview_long_michael.pdf (последний доступ: апрель 2018 г.), 2017 г.
Луккези, Р.: Спецификация файла для GEOS-5 FP. Служебная записка ГМАО № 4 (Версия 1.1), 61 стр., доступно по адресу: https://gmao.gsfc.nasa.gov/products/documents/GEOS_5_FP_File_Specification_ON4v1_1.пдф (последний доступ: апрель 2018 г.), 2017 г.
Метвен, Дж. и Хоскинс, Б.: Адвекция трассеров высокого разрешения низкими разрешение ветра, Дж. Атмос. Sci., 56, 3262–3285, 1999.
Мичалакес, Дж., Бенсон, Р., Блэк, Т., Дуда, М., Говетт, М., Хендерсон, Т., Мэдден П., Моздзински Г., Райнеке А. и Скамарок В.: Оценка Производительность и масштабируемость динамических ядер-кандидатов на будущее Глобальная система прогнозирования Generation доступна по адресу: https://www2.cisl.ucar.edu/sites/default/files/Michalakes_Slides.пдф (последний доступ: апрель 2018 г.), 2015.
Нойман, Дж. А., Трейнер, М., Айкин, К. С., Анжевин, В. М., Бриуде, Дж., Браун, С.С., Де Гау, Дж.А., Дубе, В.П., Флинн, Дж.Х., Граус, М., Холлоуэй, Дж. С., Лефер Б. Л., Неделец П., Новак Дж. Б., Пэрриш Д. Д., Поллак И. Б., Робертс Дж. М., Райерсон Т. Б., Смит Х., Туре В. и Вагнер Н. Л.: Наблюдения за переносом озона из свободной тропосферы в Лос-Анджелес бассейн, J. Geophys. Рез.-Атм., 117, D00V09, https://doi.org/10.1029/2011JD016919, 2012.
Ньюэлл, Р. Э., Туре, В., Чо, Дж. Ю. Н., Столлер, П., Маренко, А., и Смит, Х.Г.: Повсеместное распространение квазигоризонтальных слоев в тропосфере, Природа, 398, 316–319, https://doi.org/10.1038/18642, 1999. Райерсон, Т.Б., Никс, Дж.К., Флок, Ф., Робертс, Дж.М., Атлас, Э., де Гау, Дж. А., Доннелли С., Данлеа Э., Хюблер Г., Хьюи Л. Г., Шауфлер С., Таннер, Д. Дж., Варнеке, К., и Фехсенфельд, Ф.C.: Газофазный химикат характеристики азиатских эмиссионных шлейфов, наблюдаемых во время ITCT 2K2 над восточная часть северной части Тихого океана, J. Geophys. рез.-атмосфер., 109, 1–18, https://doi.org/10.1029/2003JD004488, 2004.
Одман, М. Т.: Количественный анализ численной диффузии, представленный алгоритмы адвекции в моделях качества воздуха, Atmos. Окруж., 31, 1933–1940, https://doi.org/10.1016/S1352-2310(96)00354-8, 1997.
Пекник, М.Дж. и Кейзер, Д.: Влияние пространственного разрешения на моделирование фронтогенеза верхней тропосферы с использованием сигма-координаты модель примитивных уравнений, Метеорол.Атмос. физ., 40, 137–149, https://doi.org/10.1007/BF01032454, 1989.
Поуп, В.Д., Паммент, Дж.А., Джексон, Д.Р., и Слинго, А.: представление водяного пара и его зависимость от вертикального разрешения в климатическая модель центра Хэдли, J. Clim., 14, 3065–3085, https://doi.org/10.1175/1520-0442(2001)014<3065:TROWVA>2.0.CO;2, 2001.
Путман, В.М. и Лин, С.-Дж.: Перенос конечных объемов на различных кубическая сфера сетки, J. Comput. Phys., 227, 55–78, https://doi.org/10.1016/j.jcp.2007.07.022, 2007.
Растигеев Ю., Парк Р., Бреннер М. П. и Джейкоб Д. Дж.: Решение шлейфы межконтинентального загрязнения в глобальных моделях атмосферного переноса, Дж. Геофиз. Res.-Atmos., 115, https://doi.org/10.1029/2009JD012568, 2010.
Шуберт, С. Д., Руд, Р. Б., и Пфендтнер, Дж.: Ассимилированный набор данных для Приложения наук о Земле, B. Am. метеорол. соц., 74, 2331–2342, https://doi.org/10.1175/1520-0477(1993)074<2331:AADFES>2.0.CO;2, 1993.
Семакин, А.Н. и Растигеев Ю.: Численное моделирование глобальных Атмосферный перенос химических веществ с адаптивной сеткой на основе вейвлетов высокого порядка Алгоритм уточнения, пн. Weather Rev., 144, 1469–1486, https://doi.org/10.1175/mwr-d-15-0200.1, 2016.
Штоль, А., Экхардт, С., Форстер, К., Джеймс, П. и Шпихтингер, Н.: На пути и временные рамки межконтинентального переноса загрязнения воздуха, Дж. Геофиз. Res.-Atmos., 107, 1–17, https://doi.org/10.1029/2001JD001396, 2002.
Stoller, P., Чо, Дж. Ю. Н., Ньюэлл, Р. Э., Туре, В., Чжу, Ю., Кэрролл, М. А., Альберкук, Г. М., Андерсон, Б. Е., Баррик, Дж. Д. У., Броуэлл, Э. В., Грегори Г.Л., Сакс Г.В., Вэй С., Брэдшоу Д.Д. и Сандхолм С.: Измерения атмосферных слоев с самолетов НАСА DC-8 и P-3B во время PEM-Tropics A, J. Geophys. Рез., 104, 5745, https://doi.org/10.1029/98JD02717, 1999.
Туре, В., Чо, Дж. Ю. Н., Ньюэлл, Р. Э., Маренко, А., и Смит, Х. Г. Дж.: Общие характеристики слоев, составляющих следы тропосферы, наблюдаемые в программа MOZAIC, Дж.Геофиз. Рез., 105, 17379, https://doi.org/10.1029/2000JD8, 2000.
Томпкинс, А. М. и Эмануэль, К. А.: Чувствительность вертикального разрешения смоделированная равновесная температура и профили водяного пара, QJ Roy. Метеор. Soc., 126, 1219–1238, https://doi.org/10.1002/qj.49712656502, 2000.
Ульрих, П. А., Яблоновски, К., и ван Леер, Б.: Конечный объем высокого порядка методы для уравнений мелкой воды на сфере, J. Comput. физ., 229, 6104–6134, https://doi.org/10.1016/j.jcp.2010.04.044, 2010.
Ульрих, П. А., Яблоновски, К., Рид, К. А., Зажицкий, К., Лауритцен, П. Х., Наир, Р. Д., Кент, Дж., и Верле-Банид, А.: Динамическая базовая модель Тестовый пример Проекта взаимного сравнения (DCMIP2016), 2016 г.
Уорминг, Р. Ф. и Хайетт, Б. Дж.: Подход с модифицированным уравнением к анализ устойчивости и точности конечно-разностных методов, J. Comput. Phys., 14, 159–179, https://doi.org/10.1016/0021-9991(74)-4, 1974.
Уорнер, Т.Т.: Численное прогнозирование погоды и климата, Кембриджский университет. Press, Cambridge, 2010.
Уайлд, О. и Пратер, М. Дж.: Глобальное моделирование тропосферного озона: количественная оценка ошибки из-за разрешения сетки, J. Geophys. Рез.-Атм., 111, Д11305, https://doi.org/10.1029/2005JD006605, 2006.
Ян К., Сюэ В., Фу Х., Ю Х., Ван Х., Ао Ю., Лю Ф., Ган Л., Сюй, П., и Ван, Л.: Масштабируемый полностью неявный решатель на 10 миллионов ядер для негидростатических динамики атмосферы, в: Материалы Международной конференции по Высокопроизводительные вычисления, сети, хранение и анализ, с.6. ИЭЭЭ Press, 2016.
Ю, К., Келлер, К. А., Джейкоб, Д. Дж., Молод, А. М., Истхэм, С. Д., и Лонг, М. С.: Ошибки и улучшения в использовании архивных метеорологических данных для моделирование химического переноса: анализ с использованием GEOS-Chem v11-01, управляемый Метеорология ГЕОС-5, Geosci. Модель Дев., 11, 305–319, https://doi.org/10.5194/gmd-11-305-2018, 2018.
Чжан, Л., Джейкоб, Д. Дж., Бурсма, К. Ф., Джаффе, Д. а., Олсон, Дж. Р., Боуман, К.В., Уорден, Дж.Р., Томпсон, а. М., Эйвери М.А., Коэн, Р. К., Дибб, Дж. Э., Флок Ф.М., Фьюлберг Х.Е., Хьюи Л.Г., Макмиллан В.В., Сингх Х. Б., и Вайнхаймер, А.Дж.: Транстихоокеанский перенос озонового загрязнения и влияние недавнего увеличения выбросов в Азии на качество воздуха в Северной Америке: комплексный анализ с использованием спутников, самолетов, озонозондов и наземных наблюдения, Атмос. хим. Phys., 8, 6117–6136, https://doi.org/10.5194/acp-8-6117-2008, 2008.
Чжан, Л., Джейкоб, Д.Дж., Юэ, X., Дауни, Н.В., Вуд, Д.А., и Блюитт, Д.: Источники, вносящие вклад в фоновый приземный озон в межгорных районах США. Запад, Атмос. хим. Phys., 14, 5295–5309, https://doi.org/10.5194/acp-14-5295-2014, 2014.
Zhuang, J. and Rothenberg, D.: cubedsphere: v0.1, доступный по адресу: https://doi.org/10.5281/zenodo.1095677, последний доступ: апрель 2018 г.
Zhuang, J., Jacob, D.J., and Eastham, S.D.: FV3_util: v0.1.2, доступно на: https://doi.org/10.5281/zenodo.1214605, последний доступ: апрель 2018 г.
Метод на основе геномной композиции с высоким разрешением, позволяющий различать сходные бактериальные организмы | BMC Genomics
Сравнение четырех опубликованных статистических методов
На сегодняшний день опубликовано четыре различных статистических метода для измерения отклонения использования тетрануклеотидов от их ожиданий.Метод Маркова нулевого порядка устраняет смещения частоты мононуклеотидов при случайном распределении мононуклеотидов для измерения смещения частоты тетрануклеотидов [17, 42]. Метод Маркова максимального порядка устраняет смещения компонентов для расчета смещений использования тетрануклеотидов [17, 42]. Метод z-значения, в дополнение к марковской модели максимального порядка, принимает во внимание вариации тетрануклеотидов для измерения погрешностей использования тетрануклеотидов в виде z-значений [5]. Метод относительной частоты тетрануклеотидов учитывает все систематические ошибки более низкого порядка, чтобы определить систематические ошибки использования тетрануклеотидов [20].Затем смещения использования тетрануклеотидов, рассчитанные всеми этими методами, подвергаются расчетам коэффициента корреляции Пирсона для измерения сходства состава между двумя последовательностями [5, 42].
Чтобы сравнить четыре статистических метода, мы использовали 1779 запросов (дополнительный файл 1: таблица S1) к 264 ссылкам (дополнительный файл 1: таблица S2), включающим 1964 внутривидовых и 467 692 межвидовых пары, чтобы профилировать предвзятость использования тетрануклеотидов, а затем рассчитали индекс Пирсона. коэффициенты корреляции.Поскольку состав зависит от вида [2, 9, 14, 19, 20, 21], эффективный метод должен строго отражать эту особенность. Поэтому мы сначала определили оптимальные пороговые значения коэффициента корреляции Пирсона для дифференциации видов для этих методов. Шкала F , которая ранее применялась для определения оптимальных порогов сходства последовательностей для 40 однокопийных филогенетических маркерных генов [45] и генов 16S рРНК [46] для видового разграничения прокариот, была применена для определения оптимального порога отсечки с высший балл F за видовую дифференциацию для каждого метода.Для статистического теста мы случайным образом отобрали 200 различных внутривидовых пар и 50 000 различных межвидовых пар по 10 раз для каждой выборки. Мы обнаружили, что оптимальные пороговые значения для всех этих методов были одинаковыми: 0,99 или 1,00 (дополнительный файл 2: рисунок S1). Наш парный t-критерий показал, что метод значений z дает значительно более высокие F -баллы, чем марковский метод нулевого порядка, но такие же F -баллы, как марковский метод максимального порядка и метод относительной частоты тетрануклеотидов (дополнительный файл 2: Рисунок S2).Эти результаты были дополнительно подтверждены с использованием индекса Рэнда (дополнительный файл 2: рисунки S3 и S4). В этом контексте TETRA, который вычисляет коэффициент корреляции Пирсона для z-значений, полученных методом z-значений, может использоваться в качестве репрезентативного метода для трех других опубликованных методов. Поэтому в этом исследовании мы сравнивали только TZMD с TETRA, чтобы показать высокое разрешение TZMD. Кроме того, наш дальнейший анализ показал, что подавляющее большинство внутривидовых пар с коэффициентом корреляции Пирсона > 0.99 значение коэффициента корреляции Пирсона для всех четырех методов было равно 1,00 (дополнительный файл 2: рисунок S5), что указывает на то, что они не способны различать большинство внутривидовых штаммов. Соответственно, существует явная потребность в более мощных подходах.
Предложение подхода TZMD
TETRA не может различать близкородственные виды, такие как Campylobacter jejuni и C.coli [23], и большинство внутривидовых штаммов, как показано в наших вышеприведенных данных (дополнительный файл 2: рисунок S5). ).Возможны две причины: одна состоит в том, что эти организмы почти не имеют различий по составу, а другая в том, что разрешение TETRA слишком низкое, чтобы различить эти организмы, хотя они и имеют разный состав. Мы обнаружили, что некоторая неспособность дифференцировать близкородственные виды или внутривидовые штаммы была вызвана низким разрешением TETRA. Берем внутривидовую пару Burkholderia ubonensis MSMB1189WGS и B. ubonensis RF23-BP41 и межвидовую пару B.ubonensis MSMB1189WGS и B. vietnamiensis G4 внутривидовая пара имела почти идентичный состав, что дало значение TETRA 1,00, поскольку две кривые почти полностью совпадали (рис. 1a). Тем не менее, мы обнаружили, что TETRA также дает неразличимое значение TETRA 0,99 для межвидовой пары с явно разным составом (рис. 1b) в соответствии с установленным выше пороговым значением 0,99 (дополнительный файл 2: рис. S1 и S3). Это открытие показало, что TETRA действительно имеет низкое разрешение для различения близкородственных видов, что является одним из ограничений подхода TETRA.
Рис. 1Подход TETRA не позволяет различать близкородственные виды, имеющие лишь незначительно отличающийся состав. a Для межвидовой пары. b Для внутривидовой пары с разным составом. Обрамленная четкая разница значений z, полученная из тетрануклеотидов
Одной из возможных причин низкого разрешения TETRA является то, что коэффициент корреляции Пирсона не может эффективно измерить индивидуальную разницу значений z, как показано в примере, показанном на рис.1б обведено пунктирным овалом. С математической точки зрения коэффициент корреляции Пирсона отражает общую тенденцию для всех 256 значений z, в то время как манхэттенское расстояние эффективно отражает разницу значений z для каждого отдельного тетрануклеотида (см. Методы), подразумевая, что использование манхэттенского расстояния вместо расстояния Пирсона коэффициент корреляции может улучшить разрешение для измерения разницы в составе. Соответственно, мы предложили TZMD, новый метод, использующий манхэттенское расстояние, и ожидали, что он повысит разрешение ошибок, связанных с использованием тетрануклеотидов.
При расчете значений z для 10-100% генома мы обнаружили, что тетрануклеотидное отклонение (систематическая ошибка использования, включая чрезмерное и недостаточное представление) увеличивается с размером последовательности (дополнительный файл 2: рисунок S6A), что более четко продемонстрировано с использованием накопленных тетрануклеотидных отклонений (рис. 2а). Мы показали, что размер последовательности сильно повлиял на TZMD (дополнительный файл 1: таблица S1), но не повлиял на TETRA. Чтобы исключить влияние размера последовательности, мы нормализовали z-значения, разделив их на квадратный корень размера последовательности.После нормализации последовательности разного размера из одного и того же генома ожидаемо давали аналогичные отклонения (рис. 2b и дополнительный файл 2: рисунок S6B), хотя 10 % генома давали относительно разные отклонения из-за асимметричного состава для коротких последовательностей (рис. 2b). . Это открытие показало, что наш метод нормализации верен. Таким образом, нормализованные значения z можно использовать для расчета TZMD, поскольку они точно отражают состав генома. Мы рассчитали TZMD на основе нормализованных значений z двух вышеупомянутых пар и обнаружили, что наш подход TZMD дает два различимых значения (рис.1) в соответствии с установленным ниже порогом TZMD 0,21 (см. ниже), что предварительно показывает, что TZMD имеет более высокое разрешение, чем TETRA.
Рис. 2Нормализация значений z, полученных из тетрануклеотидов. a До нормализации. b После нормализации. Приведенные здесь значения представляют накопленные тетрануклеотидные отклонения для Buchnera aphidicola str. APS ( Acyrthosiphon pisum ) (GCA_000009605.1)
Отражает максимальное геномное различие
Хотя и TETRA, и TZMD количественно определяют сходство/различие в составе, наши результаты из вышеупомянутых 1779 запросов против 264 ссылок показали, что TZMD лишь умеренно коррелирует с TZMD TETRA в мощном исполнении ( R 2 = 0.7291), что указывает на то, что TZMD — это не просто доработанная версия TETRA (рис. 3a). Соответственно, мы исследовали, является ли TZMD или TETRA более надежным отражением геномных различий. Геномные различия между двумя геномами охватывают два аспекта: процент общего генома (PSG) и среднюю нуклеотидную идентичность (ANI) общего генома. Для данной пары мы рассчитали два PSG: один для меньшего PSG (обозначен как PSG small ), а другой для большего PSG (обозначен как PSG big ).Кроме того, мы рассчитали средний ПСГ, который был средним из двух ПСГ (названный ПСГ означает ). Всего было семь различных показателей, включая ANI, PSG , малый , PSG , средний и PSG , большой для одного аспекта геномных различий, а также ANI*PSG , малый , ANI*PSG , средний и ANI*PSG . большой для двух аспектов геномных различий. Среди них ANI*PSG small представляло собой максимальную разницу между двумя геномами. Наш корреляционный анализ показал, что TZMD показал самые высокие значения R 2 для максимальных геномных различий (ANI*PSG малый ), независимо от используемого порога TZMD (рис.4а). Напротив, TETRA не давала самых высоких значений R 2 для ANI*PSG small почти при всех отсечках TETRA, кроме 0,1 (рис. 4b). Таким образом, ТЗМД всегда отражала максимальное различие, наделяя его более высокой различающей способностью, чем ТЕТРА. Кроме того, следует отметить, что значения R 2 для максимальных различий были лишь немного выше, чем для других показателей, за исключением ANI, для отдаленно родственных организмов, но относительно намного выше для близкородственных организмов (рис.4а). Этот результат указывает на то, что разница в разрешении между TZMD и TETRA возникает в первую очередь для близкородственных организмов, хотя TZMD также демонстрирует небольшое улучшение по сравнению с TETRA для дифференциации отдаленно родственных организмов.
Рис. 3Связь между TZMD и TETRA. a Корреляционный анализ между TZMD и TETRA. Слева, без логарифмического преобразования; правильно, после логарифмического преобразования. Все значения были сгенерированы с использованием 1779 запросов и 264 ссылок. b Распределение TZMD для пар с TETRA = 1, которые обведены пунктирной линией на панели A
Рис. 4TZMD отражает максимальное различие геномов. a Результаты корреляции для TZMD. b Результаты корреляции для TETRA. Всего было использовано 1779 запросов по 264 ссылкам. Результаты корреляции для организмов на уровне вида или ниже обозначены пунктирными овалами. TETRA дает самые высокие значения R 2 для измерений, отличных от максимальной разности (ANI*PSG small ), за исключением случаев, когда TETRA > 0.90 (обозначено вертикальной пунктирной линией)
Затем мы исследовали, является ли TZMD более устойчивым при различении сходных организмов на уровне видов или ниже. Отслеживание 1779 запросов по 264 ссылкам показало, что почти все внутривидовые значения TETRA были > 0,99, за двумя исключениями: одно для штаммов Borrelia hermsii CC1 и HS1 с атипичным TETRA 0,97, а другое для штаммов Borreliella burgdorferi . CA382 и B31 с нетипичным TETRA, равным 0.95. Соответственно, эти исключения имели нетипичный TZMD 0,31 и 0,42 соответственно (дополнительный файл 2: рисунок S7). За исключением этих двух пар, все другие внутривидовые пары имели максимальное значение TZMD, равное 0,27, которое использовалось в качестве порогового значения TZMD для оценки различительной способности TZMD для сходных организмов. Мы обнаружили, что TZMD дает более высокое значение R 2 при пороговом значении 0,27, чем TETRA при пороговом значении 0,99, теоретически демонстрируя, что TZMD более надежен в различении организмов на уровне видов или ниже, включая виды. принадлежащие к одному геновиду на видовом уровне и подвидам или внутривидовым штаммам ниже видового уровня.
В заключение, с теоретической точки зрения, мы продемонстрировали, что TZMD имеет более высокое разрешение, чем TETRA. Например, было обнаружено, что пары с TETRA 1,00, которые, согласно подходу TETRA, имеют полностью идентичный состав, демонстрируют различимые значения TZMD в диапазоне от 0 до 0,29 (рис. 3b), подтверждая, что TZMD имеет более высокое разрешение. чем ТЕТРА.
Незначительное улучшение видовой дифференциации
Геномный состав видоспецифичен, и внутривидовые различия, как правило, меньше, чем межвидовые [2, 9, 47, 48].Таким образом, TETRA широко применяется на уровне видов и выше, например, при метагеномном объединении [5, 28] и дифференциации видов [24]. Однако, хотя TETRA работает очень хорошо в большинстве условий, он не может различать некоторые близкородственные виды, особенно внутриродовые виды [23]. Одна из возможных причин заключается в том, что TETRA не полностью определяет геномные различия (рис. 4b). Напротив, TZMD отражает максимальную разницу между геномами. Таким образом, мы исследовали, может ли TZMD улучшить дифференциацию видов.
Для дифференциации видов мы сначала определили оптимальное пороговое значение уровня вида для TZMD. Здесь мы использовали 1779 запросов к 264 ссылкам, чтобы определить оптимальное отсечение на уровне вида. Было определено, что оптимальное отсечение составляет 0,21 с наивысшим баллом F (точность = 0,8688, полнота = 0,9949) (рис. 5a) и самым высоким индексом Рэнда (дополнительный файл 2: рисунок S8A). Используя критерий 0,21, TZMD правильно дифференцировал 1954 внутривидовых и 467 397 межвидовых пар для достижения высокого индекса Рэнда ~ 0.9994, в то время как TETRA правильно дифференцировал 1962 внутривидовых и 466 776 межвидовых или 1918 внутривидовых и 467 371 межвидовую пару для достижения относительно низкого индекса Rand ~ 0,9980 или ~ 0,9992 (дополнительный файл 2: рисунок S8B) при использовании критерия 0,99 или 1,00 соответственно (дополнительный файл 2: рисунок S1A и S3A). Для статистического теста мы случайным образом отобрали 200 различных внутривидовых пар и 50 000 различных межвидовых пар для каждой выборки 10 раз для обоих методов. Результаты показали, что оптимальное отсечение для TZMD также может быть определено при 0.21 (рис. 5b и дополнительный файл 2: рисунок S8C), что соответствовало вышеуказанному выводу (рис. 5a и дополнительный файл 2: рисунок S8A). Парный t-тест показал, что TZMD значительно превосходит TETRA (рис. 5c и дополнительный файл 2: рисунок S8D). Таким образом, с точки зрения видовой дифференциации мы продемонстрировали, что TZMD имеет более высокое разрешение, чем TETRA. Однако, по сравнению с TETRA, TZMD продемонстрировала лишь небольшое улучшение видовой дифференциации, возможно, потому, что максимальные геномные различия (ANI*PSG малый ), отраженные TZMD, лишь немного превышали PSG большой или другие показатели, отраженные TETRA для отдаленно родственные организмы (рис.4а).
Рис. 5Сравнение, основанное на показателе F , показало, что TZMD немного улучшает видовую дифференциацию. a Определение порогового значения TZMD с наивысшим баллом F . b F – баллы для 10 проб методом TZMD. c Наивысшие баллы F для подходов TZMD и TETRA. Были использованы все 1779 запросов к 264 ссылкам (панели и ). Для каждой выборки случайным образом отбирали 200 внутривидовых и 50 000 межвидовых пар (панели b и c ).Поскольку у TETRA было два критерия (0,99 или 1,00) (дополнительный файл 2: рисунки S1A и S3A), метод TETRA, использующий оба критерия, сравнивался. Штриховая линия — отсечка TZMD 0,21; P -значение, односторонний парный t-критерий
Дифференциация сходных видов, принадлежащих к одному геневиду
Близкородственные виды, такие как Escherichia coli–Shigella [24] и Bacillus anthracis–Bacillus thuringiensis–Bacillus cereus [46], были определены как единый геновид методами, основанными на общем генотипическом сходстве, такими как подход ANI.Как правило, TETRA не может различать наиболее близкородственные виды. В качестве альтернативы мы рассмотрели, может ли TZMD различать эти виды. вида Brucella были взяты в качестве примера для тестирования, так как они были выделены как единый вид методом гибридизации ДНК-ДНК из-за их > 90% значений гибридизации ДНК-ДНК [49, 50] и методом ANI из-за их > 96% ANI [46]. Мы собрали 53 полных генома из базы данных Национального центра биотехнологической информации (NCBI) (дополнительный файл 1: таблица S3) и использовали их, чтобы проверить, может ли TZMD различать сходные виды, принадлежащие к одному геновиду.Как и ожидалось, TETRA не смогла различить вида Brucella (дополнительный файл 2: рисунок S9). Однако поразительно, что TZMD четко дифференцировал все вида бруцелл (рис. 6). Кроме того, TZMD дополнительно разделил биовара B. suis на три основные клады (513UK, биовар 2 и другие биовары, включая биовары 1, 3 и 4), что согласуется с филогенетическими результатами, основанными на однонуклеотидных полиморфизмах по всему геному ( SNP), типирование мультилокусного секвенирования и выравнивание последовательностей всего генома [51].Кроме того, TZMD показал, что B. canis , возможно, произошел от клады «других биоваров» B. suis , в соответствии с результатами предыдущего исследования [52]. Кроме того, наибольшее значение TZMD составило 0,19 для пары B. vulpis F60 и B. suis bv. 1 ул. S2, затем 0,18 для пар B. vulpis F60 со всеми другими штаммами и < 0,1 для всех остальных пар (рис. 6). Следовательно, согласно его оптимальному порогу для видовой дифференциации (рис.5а), TZMD только выделила все вида Brucella как единый геновид в соответствии с предыдущими исследованиями [46, 49, 50].
Рис. 6TZMD дифференцирует бруцелл видов. вида бруцелл считаются единым геневидом. Значение TZMD используется в качестве основы для интенсивности цвета. Различные цвета названий видов указывают на разные клады. Также указаны три основные клады для B. suis . Фигура была нарисована с использованием тепловой карты.2 (пакет gplots, ward.D2 linkage)
Yersinia pseudotuberculosis – Yersinia pestis и Burkholderia mallei–Burkholderia pseudomallei , оба из которых рассматривались как единый геневид в подходе ANI [46]. как два других примера. Всего 45 полных геномов Y. pseudotuberculosis – Y. pestis (дополнительный файл 1: таблица S4) и 67 полных геномов B. mallei–B. pseudomallei (дополнительный файл 1, таблица S5) были собраны из базы данных NCBI для анализа.TETRA не смогла различить Y. pestis и Y. pseudotuberculosis (дополнительный файл 2: рисунок S10). Напротив, TZMD четко различал их (дополнительный файл 2: рисунок S11). Аналогичные результаты были получены и для B. mallei–B. pseudomallei (дополнительный файл 2: рис. S13 и S14). В заключение, все эти результаты на уровне видов продемонстрировали, что TZMD имеет более высокое разрешение, чем TETRA.
Дифференциация подвидов и внутривидовых штаммов
Затем мы проверили, можно ли использовать TZMD для дифференциации подвидов и внутривидовых штаммов. C. jejuni , один из основных пищевых патогенов в мире, вызывает энтерит или синдром Гийена-Барре у людей [53,54,55]. C. jejuni имеет два различных подвида: subsp. jejuni и subsp. дойлей [56]. Что еще более важно, оба подвида были полностью секвенированы. Кроме того, были определены полные геномы многочисленных штаммов C. jejuni [23]. Поэтому для изучения этого вопроса был выбран C. jejuni .Мы собрали все 39 полных геномов C. jejuni из базы данных NCBI (дополнительный файл 1: таблица S6), один для subsp. дойлей и остальные для подсп. еджуни . Наши результаты показали, что подход TZMD четко различал два подвида, а также внутривидовые штаммы (рис. 7), в то время как подход TETRA не мог различать ни один штамм или даже подвид (дополнительный файл 2: рисунок S14).
Рис. 7TZMD дифференцирует подвидовые и внутривидовые штаммы Campylobacter jejuni .Значение TZMD используется в качестве основы для интенсивности цвета. Коробочные, клональные штаммы; синяя полоса, подсп. дойлей ; голубая полоса, subsp. еджуни . Рисунок был нарисован с использованием функции Heatmap.2 (пакет gplots, связь ward.D2)
Francisella tularensis имеет несколько подвидов, включая subsp. novicida , подвид. holarctica и подвид. tularensis , которые были выбраны для дальнейшего сравнения способности TZMD и TETRA различать подвиды.Всего было собрано 33 полных генома (дополнительный файл 1: таблица S7). TZMD четко различал все подвиды (дополнительный файл 2: рисунок S15), в то время как TETRA не мог различать подвиды. holarctica и подвид. novicida (дополнительный файл 2: рисунок S16).
Для дальнейшего сравнения возможностей TZMD и TETRA для различения внутривидовых штаммов.TZMD четко различал внутривидовые штаммы S. pyogenes (дополнительный файл 2: рисунок S17), в то время как TETRA не мог дифференцировать ни один штамм S. pyogenes (дополнительный файл 2: рисунок S18). Аналогичные результаты были также получены для B. cereus (дополнительный файл 2: рисунки S19 и S20).
Кроме того, мы обнаружили, что подход TZMD дополнительно различает клональные и неклональные штаммы для клональных штаммов со значением TZMD 0 и неклональных штаммов со значением TZMD > 0 (рис.7 и дополнительный файл 2: рисунок S17 и S19). Суммирование всех пар со значением TZMD, равным 0, из 1779 запросов и 264 ссылок показало, что этот стандарт содержит значительно больше информации.

